北京市昌平区2022届高三数学二模试卷

试卷更新日期：2022-06-27 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知集合 $A = {x | 0 < x < 2} ， B = {x | x \geq 1}$ ，则 $A ∪ B =$ （）

A、 ${x | x > 0}$ B、 ${x | 1 \leq x < 2}$ C、 ${x | x \geq 1}$ D、 ${x | 0 < x < 2}$

查看试题解析
2. 设复数z满足 $(1 - i) z = 2 i$ ，则z= （）

A、-1+i B、-1-i C、1+i D、1-i

查看试题解析
3. 为倡导“节能减排，低碳生活”的理念，某社区对家庭的人均月用电量情况进行了调查，通过抽样，获得了某社区100个家庭的人均月用电量（单位：千瓦时），将数据按照 $[40 ， 60) ， [60 ， 80) ， [80 ， 100) ， [100 ， 120) ， [120 ， 140) ， [140 ， 160]$ 分成6组，制成了如图所示的频率分布直方图. 若该社区有3000个家庭，估计全社区人均月用电量低于80千瓦时的家庭数为（）

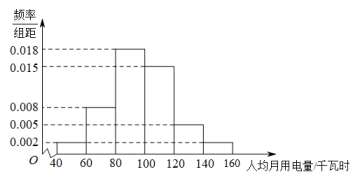A、300 B、450 C、480 D、600

查看试题解析
4. 记 $S_{n}$ 为等差数列 ${a_{n}}$ 的前 $n$ 项和，若 $S_{3} = a_{5} ， a_{2} - a_{1} = 2$ ，则 $a_{4} =$ （）

A、4 B、7 C、8 D、9

查看试题解析
5. 已知双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的焦距为 $4$ ，其右焦点到双曲线 $C$ 的一条渐近线的距离为 $\sqrt{2}$ ，则双曲线 $C$ 的渐近线方程为（）

A、 $y = \pm 2 x$ B、 $y = \pm \sqrt{3} x$ C、 $y = \pm \sqrt{2} x$ D、 $y = \pm x$

查看试题解析
6. “ $θ = \frac{π}{2}$ ”是“函数 $f (x) = s i n (x + θ)$ 在区间 $(0 ， \frac{π}{2})$ 上单调递减”的（）

A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
7. 如图，在正四棱柱 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $O$ 是底面 $A B C D$ 的中心， $E ， F$ 分别是 $B B_{1} ， D D_{1}$ 的中点，则下列结论正确的是（）

A、 $A_{1} O$ // $E F$ B、 $A_{1} O ⊥ E F$ C、 $A_{1} O$ //平面 $E F B_{1}$ D、 $A_{1} O ⊥$ 平面 $E F B_{1}$

查看试题解析
8. 已知直线 $l ： a x - y + 1 = 0$ 与圆 $C ： (x - 1)^{2} + y^{2} = 4$ 相交于两点 $A ， B$ ，当 $a$ 变化时，△ $A B C$ 的面积的最大值为（）

A、1 B、 $\sqrt{2}$ C、2 D、 $2 \sqrt{2}$

查看试题解析
9. 已知函数 $f (x) = a x^{2} - 4 a x + 2 (a < 0)$ ，则关于 $x$ 的不等式 $f (x) > l o g_{2} x$ 的解集是（）

A、 $(- \infty ， 4)$ B、 $(0 ， 1)$ C、 $(0 ， 4)$ D、 $(4 ， + \infty)$

查看试题解析
10. 在△ $A B C$ 中， $∠ B = 4 5^{°} ， c = 4 ，$ 只需添加一个条件，即可使△ $A B C$ 存在且唯一.条件：① $a = 3 \sqrt{2}$ ； ② $b = 2 \sqrt{5}$ ；③ $c o s C = - \frac{4}{5}$ 中，所有可以选择的条件的序号为（）

A、① B、①② C、②③ D、①②③

查看试题解析

二、填空题

11. 抛物线 $y^{2} = 2 x$ 的准线方程为．

查看试题解析
12. ${(2 x - \frac{1}{\sqrt{x}})}^{6}$ 展开式中常数项为（用数字作答）.

查看试题解析
13. 若函数 $f (x) = {\begin{array}{l} 2^{x} - b ， x < 0 ， \\ \sqrt{x} ， x \geq 0 \end{array}$ 有且仅有两个零点，则实数 $b$ 的一个取值为.

查看试题解析
14. 已知 $D$ 是△ $A B C$ 的边 $A B$ 的中点， $| \vec{A B} | = 3 ， | \vec{A C} | = 2 ，$ ， $∠ C A B = \frac{π}{3}$ ，则 $\vec{A B} \cdot \vec{A C} =$ ； $\vec{D B} \cdot \vec{D C} =$

查看试题解析
15. 刺绣是中国优秀的民族传统工艺之一，已经有2000多年的历史.小王同学在刺绣选修课上，设计了一个螺旋形图案--即图中的阴影部分.它的设计方法是：先画一个边长为3的正三角形 $A_{1} B_{1} C_{1}$ ，取正三角形 $A_{1} B_{1} C_{1}$ 各边的三等分点 $A_{2 ，} ， B_{2} ， C_{2}$ ，得到第一个阴影三角形 $A_{2} B_{1} B_{2}$ ；在正三角形 $A_{2} B_{2} C_{2}$ 中，再取各边的三等分点 $A_{3} ， B_{3} ， C_{3}$ ，得到第二个阴影三角形 $A_{3} B_{2} B_{3}$ ；继续依此方法，直到得到图中的螺旋形图案，则 $A_{3} B_{2} =$ ；图中螺旋形图案的面积为.

查看试题解析

三、解答题

16. 如图，在棱长为 $2$ 的正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，点 $M$ 是 $B C$ 的中点.

(1)、求证： $A B_{1} ⊥$ 平面 $A_{1} B M$ ；

(2)、求二面角 $B - A_{1} M - C_{1}$ 的大小；

(3)、求点 $A$ 到平面 $A_{1} M C_{1}$ 的距离.

查看试题解析
17. 已知函数 $f (x) = A s i n (ω x + ϕ) (A > 0 ， ω > 0 ， | ϕ | < \frac{π}{2})$ ，且 $f (x)$ 的最小正周期为 $π$ ，再从条件①、条件②、条件③中选择两个作为一组已知条件.

(1)、求 $f (x)$ 的解析式；

(2)、设 $g (x) = f (x) + 2 \sqrt{2} c o s 2 x$ ，若 $g (x)$ 在区间 $[0 ， m]$ 上的最大值为2，求 $m$ 的最小值．
条件①： $f (x)$ 的最小值为-2；
条件②： $f (x)$ 的图象经过点 $(\frac{π}{2} ， \sqrt{2})$ ；
条件③；直线 $x = \frac{3 π}{8}$ 是函数 $f (x)$ 的图象的一条对称轴.
注：如果选择多组符合要求的条件分别解答，按第一个解答计分．

查看试题解析
18. 某产业园生产的一种产品的成本为50元/件.销售单价依产品的等级来确定，其中优等品、一等品、二等品、普通品的销售单价分别为80元、75元、65元、60元.为了解各等级产品的比例，检测员从流水线上随机抽取200件产品进行等级检测，检测结果如下表所示.
产品等级
优等品
一等品
二等品
普通品
样本数量（件）
30
50
60
60

(1)、若从流水线上随机抽取一件产品，估计该产品为优等品的概率；

(2)、从该流水线上随机抽取3件产品，记其中单件产品利润大于20元的件数为 $X$ ，用频率估计概率，求随机变量 $X$ 的分布列和数学期望；

(3)、为拓宽市场，产业园决定对抽取的200件样本产品进行让利销售，每件产品的销售价格均降低了5元.设降价前后这200件样本产品的利润的方差分别为 ${s_{1}}^{2} ， {s_{2}}^{2}$ ，比较 ${s_{1}}^{2} ， {s_{2}}^{2}$ 的大小.（请直接写出结论）

查看试题解析
19. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的离心率为 $\frac{\sqrt{2}}{2}$ ，上下顶点分别为 $A ， B$ ，且 $| A B | = 4$ .过点 $(0 ， 1)$ 的直线与椭圆 $C$ 相交于不同的两点 $M ， N$ （不与点 $A ， B$ 重合）.

(1)、求椭圆 $C$ 的方程；

(2)、若直线 $A M$ 与直线 $y = 4$ 相交于点 $P$ ，求证： $B ， P ， N$ 三点共线.

查看试题解析
20. 已知函数 $f (x) = a l n x - b x + b$ ， $g (x) = \frac{e^{x}}{x} - a (x > 0)$ .

(1)、若曲线 $y = f (x)$ 与曲线 $y = g (x)$ 在它们的交点 $(1 ， c)$ 处具有公共切线，求实数 $a ， b$ 的值；

(2)、若函数 $g (x)$ 无零点，求实数 $a$ 的取值范围；

(3)、当 $a = b$ 时，函数 $F (x) = f (x) + g (x)$ 在 $x = 1$ 处取得极小值，求实数 $a$ 的取值范围.

查看试题解析
21. 已知数列 ${a_{n}}$ ，给出两个性质：
①对于任意的 $i \in N^{*}$ ，存在 $k_{i} \in R$ ，当 $j > i ， j \in N^{*}$ 时，都有 $a_{j} - a_{i} \geq k_{i} (j - i)$ 成立；
②对于任意的 $i \in N^{*} ， i \geq 2$ ，存在 $k_{i} \in R$ ，当 $j < i ， j \in N^{*}$ 时，都有 $a_{j} - a_{i} \geq k_{i} (j - i)$ 成立．

(1)、已知数列 ${a_{n}}$ 满足性质①，且 $k_{i} = 2 (i \in N^{*})$ ， $a_{1} = 1 ， a_{4} = 7$ ，试写出 $a_{2} ， a_{3}$ 的值；

(2)、已知数列 ${b_{n}}$ 的通项公式为 $b_{n} = 3 \times 2^{n - 1}$ ，证明：数列 ${b_{n}}$ 满足性质①；

(3)、若数列 ${c_{n}}$ 满足性质①②，且当 $i \in N^{*} ， i \geq 2$ 时，同时满足性质①②的 $k_{i}$ 存在且唯一.证明：数列 ${c_{n}}$ 是等差数列．

查看试题解析

产品等级	优等品	一等品	二等品	普通品
样本数量（件）	30	50	60	60