湖南省娄底市2022年中考数学试卷
试卷更新日期:2022-06-24 类型:中考真卷
一、单选题
-
1. 2022的倒数是( )A、2022 B、-2022 C、 D、2. 下列式子正确的是( )A、 B、 C、 D、3. 一个小组10名同学的出生年份(单位:月)如下表所示:
编号
1
2
3
4
5
6
7
8
9
10
月份
2
6
8
6
10
4
7
8
8
7
这组数据(月份)的众数是( )
A、10 B、8 C、7 D、64. 下列与2022年冬奥会相关的图案中,是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 5. 截至2022年6月2日,世界第四大水电站——云南昭通溪洛渡水电站累计生产清洁电能突破5000亿千瓦时,相当于替代标准煤约1.52亿吨,减排二氧化碳约4.16亿.5000亿用科学记数法表示为( )
5. 截至2022年6月2日,世界第四大水电站——云南昭通溪洛渡水电站累计生产清洁电能突破5000亿千瓦时,相当于替代标准煤约1.52亿吨,减排二氧化碳约4.16亿.5000亿用科学记数法表示为( ) A、 B、 C、 D、6. 一条古称在称物时的状态如图所示,已知 , 则( )
A、 B、 C、 D、6. 一条古称在称物时的状态如图所示,已知 , 则( )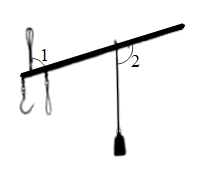 A、 B、 C、 D、7. 不等式组的解集在数轴上表示正确的是( )A、
A、 B、 C、 D、7. 不等式组的解集在数轴上表示正确的是( )A、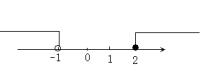 B、
B、 C、
C、 D、
D、 8. 将直线向上平移2个单位,相当于( )A、向左平移2个单位 B、向左平移1个单位 C、向右平移2个单位 D、向右平移1个单位9. 在古代,人们通过在绳子上打结来计数.即“结绳计数”.当时有位父亲为了准确记录孩子的出生天数,在粗细不同的绳子上打结(如图),由细到粗(右细左粗),满七进一,那么孩子已经出生了( )
8. 将直线向上平移2个单位,相当于( )A、向左平移2个单位 B、向左平移1个单位 C、向右平移2个单位 D、向右平移1个单位9. 在古代,人们通过在绳子上打结来计数.即“结绳计数”.当时有位父亲为了准确记录孩子的出生天数,在粗细不同的绳子上打结(如图),由细到粗(右细左粗),满七进一,那么孩子已经出生了( ) A、1335天 B、516天 C、435天 D、54天10. 如图,等边内切的图形来自我国古代的太极图,等边三角形内切圆中的黑色部分和白色部分关于等边的内心成中心对称,则圆中的黑色部分的面积与的面积之比是( )
A、1335天 B、516天 C、435天 D、54天10. 如图,等边内切的图形来自我国古代的太极图,等边三角形内切圆中的黑色部分和白色部分关于等边的内心成中心对称,则圆中的黑色部分的面积与的面积之比是( ) A、 B、 C、 D、11. 在平面直角坐标系中,为坐标原点,已知点、(且),过点、的直线与两坐标轴相交于、两点,连接、 , 则下列结论中成立的是( )
A、 B、 C、 D、11. 在平面直角坐标系中,为坐标原点,已知点、(且),过点、的直线与两坐标轴相交于、两点,连接、 , 则下列结论中成立的是( )①点、在反比例函数的图象上;②成等腰直角三角形;③;④的值随的增大而增大.
A、②③④ B、①③④ C、①②④ D、①②③12. 若 , 则称是以10为底的对数.记作:.例如: , 则; , 则.对数运算满足:当 , 时, , 例如: , 则的值为( )A、5 B、2 C、1 D、0二、填空题
-
13. 函数的自变量的取值范围是.14. 已知实数是方程的两根,则.15. 黑色袋子中装有质地均匀,大小相同的编号为1~15号台球共15个,搅拌均匀后,从袋中随机摸出1个球,则摸出的球编号为偶数的概率是.16. 九年级融融陪同父母选购家装木地板,她感觉某品牌木地板拼接图(如实物图)比较美观,通过手绘(如图)、测量、计算发现点是的黄金分割点,即.延长与相交于点 , 则.(精确到0.001)
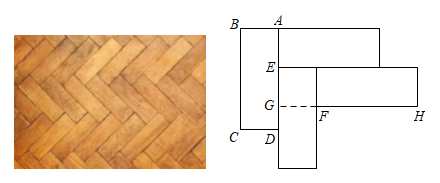 17. 菱形的边长为2, , 点、分别是、上的动点,的最小值为.
17. 菱形的边长为2, , 点、分别是、上的动点,的最小值为.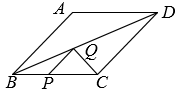 18. 如图,已知等腰的顶角的大小为 , 点D为边上的动点(与、不重合),将绕点A沿顺时针方向旋转角度时点落在处,连接.给出下列结论:①;②;③当时,的面积取得最小值.其中正确的结论有(填结论对应的序号).
18. 如图,已知等腰的顶角的大小为 , 点D为边上的动点(与、不重合),将绕点A沿顺时针方向旋转角度时点落在处,连接.给出下列结论:①;②;③当时,的面积取得最小值.其中正确的结论有(填结论对应的序号).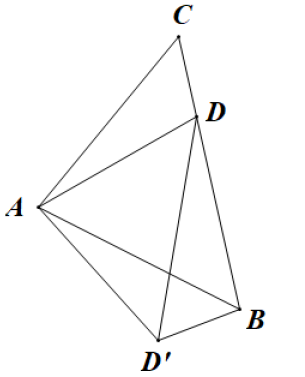
三、解答题
-
19. 计算:.20. 先化简,再求值: , 其中是满足条件的合适的非负整数.21. 按国务院教育督导委员会办公室印发的《关于组织责任督学进行“五项管理”督导的通知》要求,各中小学校积极行动,取得了良好的成绩.某中学随机抽取了部分学生对他们一周的课外阅读时间(:10h以上,:8h~10h,:6h~8h,:6h以下)进行问卷调查,将所得数据进行分类,统计了绘制了如下不完整的统计图.请根据图中的信息,解答下列问题:
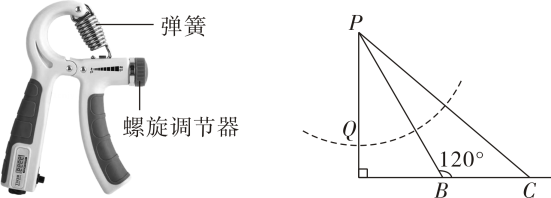
 (1)、本次调查的学生共名;(2)、 , ;(3)、补全条形统计图.22. “体育承载着国家强盛、民族振兴的梦想”.墩墩使用握力器(如实物图所示)锻炼手部肌肉.如图,握力器弹簧的一端固定在点处,在无外力作用下,弹簧的长度为 , 即.开始训练时,将弹簧的端点调在点处,此时弹簧长 , 弹力大小是 , 经过一段时间的锻炼后,他手部的力量大大提高,需增加训练强度,于是将弹簧端点调到点处,使弹力大小变为 , 已知 , 求的长.
(1)、本次调查的学生共名;(2)、 , ;(3)、补全条形统计图.22. “体育承载着国家强盛、民族振兴的梦想”.墩墩使用握力器(如实物图所示)锻炼手部肌肉.如图,握力器弹簧的一端固定在点处,在无外力作用下,弹簧的长度为 , 即.开始训练时,将弹簧的端点调在点处,此时弹簧长 , 弹力大小是 , 经过一段时间的锻炼后,他手部的力量大大提高,需增加训练强度,于是将弹簧端点调到点处,使弹力大小变为 , 已知 , 求的长.注:弹簧的弹力与形变成正比,即 , 是劲度系数,是弹簧的形变量,在无外力作用下,弹簧的长度为 , 在外力作用下,弹簧的长度为 , 则.
 23. “绿水青山就是金山银山”.科学研究表明:树叶在光合作用后产生的分泌物能够吸附空气中的悬浮颗粒物,具有滞尘净化空气的作用.已知一片银杏树叶一年的平均滞尘量比一片国槐树叶一年的平均滞尘量的2倍少 , 若一片国槐树叶与一片银杏树叶一年的平均滞尘总量为.(1)、请分别求出一片国槐树叶和一片银杏树叶一年的平均滞尘量;(2)、娄底市双峰县九峰山森林公园某处有始于唐代的三棵银杏树,据估计三棵银杏树共有约50000片树叶.问这三棵银杏树一年的平均滞尘总量约多少千克?24. 如图,以为边分别作菱形和菱形(点 , , 共线),动点在以为直径且处于菱形内的圆弧上,连接交于点.设.
23. “绿水青山就是金山银山”.科学研究表明:树叶在光合作用后产生的分泌物能够吸附空气中的悬浮颗粒物,具有滞尘净化空气的作用.已知一片银杏树叶一年的平均滞尘量比一片国槐树叶一年的平均滞尘量的2倍少 , 若一片国槐树叶与一片银杏树叶一年的平均滞尘总量为.(1)、请分别求出一片国槐树叶和一片银杏树叶一年的平均滞尘量;(2)、娄底市双峰县九峰山森林公园某处有始于唐代的三棵银杏树,据估计三棵银杏树共有约50000片树叶.问这三棵银杏树一年的平均滞尘总量约多少千克?24. 如图,以为边分别作菱形和菱形(点 , , 共线),动点在以为直径且处于菱形内的圆弧上,连接交于点.设.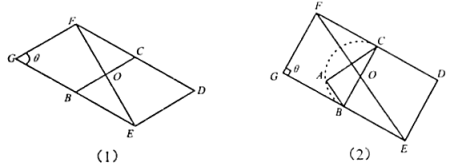 (1)、求证:无论为何值,与相互平分;并请直接写出使成立的值.(2)、当时,试给出的值,使得垂直平分 , 请说明理由.
(1)、求证:无论为何值,与相互平分;并请直接写出使成立的值.(2)、当时,试给出的值,使得垂直平分 , 请说明理由.


