湖北省随州市2022年中考数学试卷
试卷更新日期:2022-06-24 类型:中考真卷
一、单选题
-
1. 2022的倒数是( )A、2022 B、-2022 C、 D、2. 如图,直线// , 直线l与 , 相交,若图中则∠2为( )
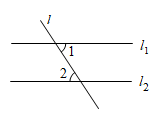 A、30° B、40° C、50° D、60°3. 小明同学连续5次测验的成绩分别为:97,97,99,101,106(单位:分),则这组数据的众数和平均数分别为( )A、97和99 B、97和100 C、99和100 D、97和1014. 如图是一个放在水平桌面上的半球体,该几何体的三视图中完全相同的是( )
A、30° B、40° C、50° D、60°3. 小明同学连续5次测验的成绩分别为:97,97,99,101,106(单位:分),则这组数据的众数和平均数分别为( )A、97和99 B、97和100 C、99和100 D、97和1014. 如图是一个放在水平桌面上的半球体,该几何体的三视图中完全相同的是( ) A、主视图和左视图 B、主视图和俯视图 C、左视图和俯视图 D、三个视图均相同5. 我国元朝朱世杰所著的《算学启蒙》中记载:“良马日行二百四十里,驽马日行一百五十里.驽马先行一十二日,问良马几何追及之.”意思是:“跑得快的马每天走240里,跑得慢的马每天走150里,慢马先走12天,快马几天可以追上慢马?”若设快马x天可以追上慢马,则可列方程为( )A、 B、 C、 D、6. 2022年6月5日10时44分07秒,神舟十四号飞船成功发射,将陈冬、刘洋、蔡旭哲三位宇航员送入了中国空间站.已知中国空间站绕地球运行的速度约为 , 则中国空间站绕地球运行走过的路程(m)用科学记数法可表示为( )A、 B、 C、 D、7. 已知张强家、体育场、文具店在同一直线上.下面的图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后散步走回家.图中x表示时间,y表示张强离家的距离.则下列结论不正确的是( )
A、主视图和左视图 B、主视图和俯视图 C、左视图和俯视图 D、三个视图均相同5. 我国元朝朱世杰所著的《算学启蒙》中记载:“良马日行二百四十里,驽马日行一百五十里.驽马先行一十二日,问良马几何追及之.”意思是:“跑得快的马每天走240里,跑得慢的马每天走150里,慢马先走12天,快马几天可以追上慢马?”若设快马x天可以追上慢马,则可列方程为( )A、 B、 C、 D、6. 2022年6月5日10时44分07秒,神舟十四号飞船成功发射,将陈冬、刘洋、蔡旭哲三位宇航员送入了中国空间站.已知中国空间站绕地球运行的速度约为 , 则中国空间站绕地球运行走过的路程(m)用科学记数法可表示为( )A、 B、 C、 D、7. 已知张强家、体育场、文具店在同一直线上.下面的图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后散步走回家.图中x表示时间,y表示张强离家的距离.则下列结论不正确的是( )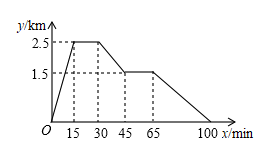 A、张强从家到体育场用了15min B、体育场离文具店1.5km C、张强在文具店停留了20min D、张强从文具店回家用了35min8. 七巧板是一种古老的中国传统智力玩具,如图,在正方形纸板ABCD中,BD为对角线,E,F分别为BC,CD的中点,分别交BD,EF于O,P两点,M,N分别为BO,DC的中点,连接AP,NF,沿图中实线剪开即可得到一副七巧板,则在剪开之前,关于该图形,下列说法:①图中的三角形都是等腰直角三角形;②四边形MPEB是菱形;③四边形PFDM的面积占正方形ABCD面积的.正确的有( )
A、张强从家到体育场用了15min B、体育场离文具店1.5km C、张强在文具店停留了20min D、张强从文具店回家用了35min8. 七巧板是一种古老的中国传统智力玩具,如图,在正方形纸板ABCD中,BD为对角线,E,F分别为BC,CD的中点,分别交BD,EF于O,P两点,M,N分别为BO,DC的中点,连接AP,NF,沿图中实线剪开即可得到一副七巧板,则在剪开之前,关于该图形,下列说法:①图中的三角形都是等腰直角三角形;②四边形MPEB是菱形;③四边形PFDM的面积占正方形ABCD面积的.正确的有( )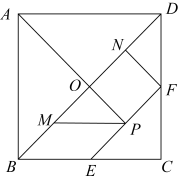 A、只有① B、①② C、①③ D、②③9. 如图,已知点B,D,C在同一直线的水平,在点C处测得建筑物AB的顶端A的仰角为α,在点D处测得建筑物AB的顶端A的仰角为β, , 则建筑物AB的高度为( )
A、只有① B、①② C、①③ D、②③9. 如图,已知点B,D,C在同一直线的水平,在点C处测得建筑物AB的顶端A的仰角为α,在点D处测得建筑物AB的顶端A的仰角为β, , 则建筑物AB的高度为( ) A、 B、 C、 D、10. 如图,已知开口向下的抛物线与x轴交于点对称轴为直线.则下列结论:①;②;③函数的最大值为;④若关于x的方数无实数根,则.正确的有( )
A、 B、 C、 D、10. 如图,已知开口向下的抛物线与x轴交于点对称轴为直线.则下列结论:①;②;③函数的最大值为;④若关于x的方数无实数根,则.正确的有( )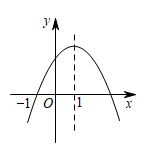 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
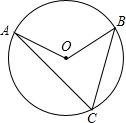
11. 计算:.12. 如图,点A,B,C都在⊙O上,∠ACB=60°,则∠AOB的度数为.
 13. 已知二元一次方程组 , 则的值为.14. 如图,在平面直角坐标系中,直线与x轴,y轴分别交于点A,B,与反比例函数的图象在第一象限交于点C,若 , 则k的值为.
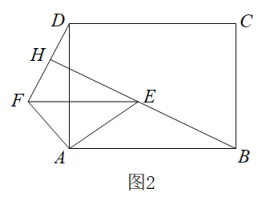
13. 已知二元一次方程组 , 则的值为.14. 如图,在平面直角坐标系中,直线与x轴,y轴分别交于点A,B,与反比例函数的图象在第一象限交于点C,若 , 则k的值为. 15. 已知m为正整数,若是整数,则根据可知m有最小值.设n为正整数,若是大于1的整数,则n的最小值为 , 最大值为.16. 如图1,在矩形ABCD中, , , E,F分别为AB,AD的中点,连接EF.如图2,将△AEF绕点A逆时针旋转角 , 使 , 连接BE并延长交DF于点H,则∠BHD的度数为 , DH的长为.
15. 已知m为正整数,若是整数,则根据可知m有最小值.设n为正整数,若是大于1的整数,则n的最小值为 , 最大值为.16. 如图1,在矩形ABCD中, , , E,F分别为AB,AD的中点,连接EF.如图2,将△AEF绕点A逆时针旋转角 , 使 , 连接BE并延长交DF于点H,则∠BHD的度数为 , DH的长为.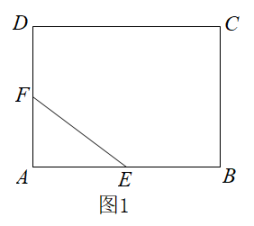
三、解答题
-
17. 解分式方程:.18. 已知关于x的一元二次方程有两个不等实数根 , .(1)、求k的取值范围;(2)、若 , 求k的值.19. 如图,在平行四边形ABCD中,点E,F分别在边AB,CD上,且四边形BEDF为正方形.
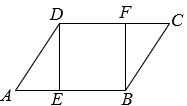 (1)、求证;(2)、已知平行四边形ABCD的面积为 , .求的长.20. 为落实国家“双减”政策,立德中学在课后托管时间里开展了“音乐社团、体育社团、文学社团,美术社团”活动.该校从全校600名学生中随机抽取了部分学生进行“你最喜欢哪一种社团活动(每人必选且只选一种)”的问卷调查,根据调查结果,绘制了如图所示的两幅不完整的统计图.
(1)、求证;(2)、已知平行四边形ABCD的面积为 , .求的长.20. 为落实国家“双减”政策,立德中学在课后托管时间里开展了“音乐社团、体育社团、文学社团,美术社团”活动.该校从全校600名学生中随机抽取了部分学生进行“你最喜欢哪一种社团活动(每人必选且只选一种)”的问卷调查,根据调查结果,绘制了如图所示的两幅不完整的统计图.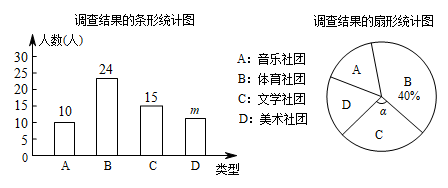
根据图中信息,解答下列问题
(1)、参加问卷调查的学生共有人;(2)、条形统计图中m的值为 , 扇形统计图中的度数为;(3)、根据调查结果,可估计该校600名学生中最喜欢“音乐社团”的约有人;(4)、现从“文学社团”里表现优秀的甲、乙、丙、丁四名同学中随机选取两名参加演讲比赛,请用列表或画树状图的方法求出恰好选中甲和乙两名同学的概率.21. 如图,已知D为⊙O上一点,点C在直径BA的延长线上,BE与⊙O相切,交CD的延长线于点E,且. (1)、判断CD与⊙O的位置关系,并说明理由;(2)、若 , ,
(1)、判断CD与⊙O的位置关系,并说明理由;(2)、若 , ,①求⊙O的半径;
②求BD的长.
22. 2022年的冬奥会在北京举行,其中冬奥会古祥物“冰墩墩”深受人们喜爱,多地出现了“一墩难求”的场面,某纪念品商店在开始售卖当天提供150个“冰墩墩”后很快就被抢购一空.该店决定让当天未购买到的顾客可通过预约在第二天优先购买,并且从第二天起,每天比前一天多供应m个(m为正整数)经过连续15天的销售统计,得到第x天( , 且x为正整数)的供应量(单位:个)和需求量(单位:个)的部分数据如下表,其中需求量与x满足某二次函数关系.(假设当天预约的顾客第二天都会购买,当天的需求量不包括前一天的预约数)第x天
1
2
…
6
…
11
…
15
供应量(个)
150
…
…
…
需求量(个)
220
229
…
245
…
220
…
164
(1)、直接写出与x和与x的函数关系式;(不要求写出x的取值范围)(2)、已知从第10天开始,有需求的顾客都不需要预约就能购买到(即前9天的总需求量超过总供应量,前10天的总需求量不超过总供应量),求m的值;(参考数据:前9天的总需求量为2136个)(3)、在第(2)问m取最小值的条件下,若每个“冰墩墩”售价为100元,求第4天与第12天的销售额.23. 《几何原本》是古希腊数学家欧几里得的一部不朽著作,是数学发展史的一个里程碑.在该书的第2幕“几何与代数”部分,记载了很多利用几何图形来论证的代数结论,利用几何给人以强烈印象将抽象的逻辑规律体现在具体的图形之中.(1)、我们在学习许多代数公式时,可以用几何图形来推理,观察下列图形,找出可以推出的代数公式,(下面各图形均满足推导各公式的条件,只需填写对应公式的序号)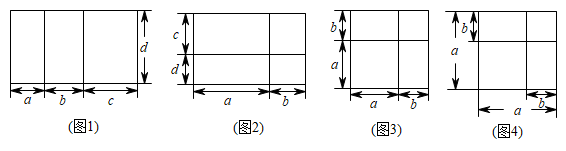
公式①:
公式②:
公式③:
公式④:
图1对应公式 , 图2对应公式 , 图3对应公式 , 图4对应公式;
(2)、《几何原本》中记载了一种利用几何图形证明平方差公式的方法,如图5,请写出证明过程;(已知图中各四边形均为矩形)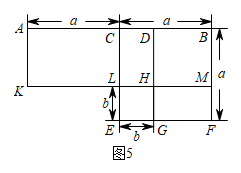 (3)、如图6,在等腰直角三角形ABC中, , D为BC的中点,E为边AC上任意一点(不与端点重合),过点E作于点G,作F点H过点B作BF//AC交EG的延长线于点F.记△BFG与△CEG的面积之和为 , △ABD与△AEH的面积之和为.
(3)、如图6,在等腰直角三角形ABC中, , D为BC的中点,E为边AC上任意一点(不与端点重合),过点E作于点G,作F点H过点B作BF//AC交EG的延长线于点F.记△BFG与△CEG的面积之和为 , △ABD与△AEH的面积之和为.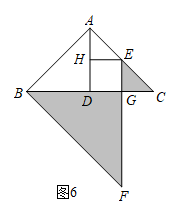
①若E为边AC的中点,则的值为 ▲ ;
②若E不为边AC的中点时,试问①中的结论是否仍成立?若成立,写出证明过程;若不成立,请说明理由.
24. 如图1,平面直角坐标系xOy中,抛物线与x轴分则点A和点 , 与y轴交于点C,对称轴为直线 , 且 , P为抛物线上一动点.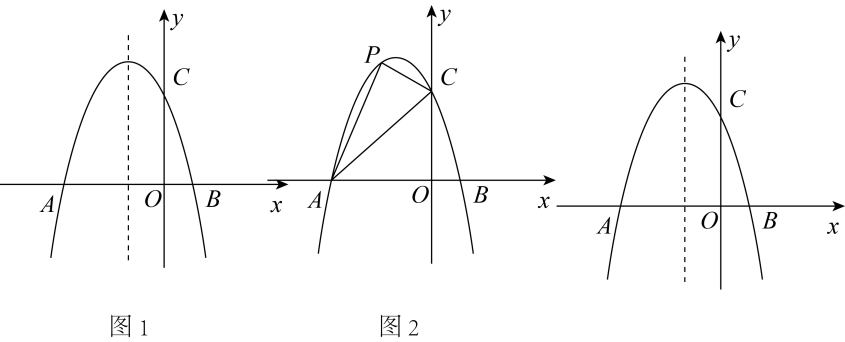 (1)、直接写出抛物线的解析式;(2)、如图2,连接AC,当点P在直线AC上方时,求四边形PABC面积的最大值,并求出此时P点的坐标;(3)、设M为抛物线对称轴上一动点,当P,M运动时,在坐标轴上是否存在点N,使四边形PMCN为矩形?若存在,直接写出点P及其对应点N的坐标;若不存在,请说明理由.
(1)、直接写出抛物线的解析式;(2)、如图2,连接AC,当点P在直线AC上方时,求四边形PABC面积的最大值,并求出此时P点的坐标;(3)、设M为抛物线对称轴上一动点,当P,M运动时,在坐标轴上是否存在点N,使四边形PMCN为矩形?若存在,直接写出点P及其对应点N的坐标;若不存在,请说明理由.