湖北省武汉市2022届高三下学期数学五月模拟试卷（二）

试卷更新日期：2022-06-24 类型：高考模拟

进入出卷网下载

一、选择题

1. 设集合 $A = {x | x^{2} - 3 x + 2 > 0}$ ，集合 $B = {x | 2 x - 3 < 0}$ ，则 $A ∩ B =$ （）

A、 $(- \infty ， \frac{3}{2}) ∪ (2 ， + \infty)$ B、 $(- \infty ， 1)$ C、 $(- \infty ， 1) ∪ (2 ， + \infty)$ D、 $(- \infty ， \frac{3}{2})$

查看试题解析
2. 已知 $a = 202 3^{\frac{1}{2022}}$ ， $b = l o g_{2023} 2022$ ， $c = l o g_{2022} \frac{1}{2023}$ ，则a，b，c的大小关系是（）

A、 $a > b > c$ B、 $b > a > c$ C、 $c > a > b$ D、 $a > c > b$

查看试题解析
3. 已知 $s i n θ + c o s θ = - \frac{1}{5}$ ， $θ \in (0 ， π)$ ，则 $s i n θ - c o s θ =$ （）

A、 $\frac{1}{5}$ B、 $- \frac{1}{5}$ C、 $\frac{7}{5}$ D、 $- \frac{7}{5}$

查看试题解析
4. 设公差不为零的等差数列 ${a_{n}}$ 的前n项和为 $S_{n}$ ， $a_{4} = 2 a_{5}$ ，则 $\frac{S_{7}}{S_{4}} =$ （）

A、 $\frac{7}{4}$ B、-1 C、1 D、 $\frac{5}{4}$

查看试题解析
5. 2021年12月22日教育部提出五项管理“作业、睡眠、手机、课外阅读、健康管理”，体育锻炼是五项管理中一个非常重要的方面，各地中小学积极响应教育部政策，改善学生和教师锻炼设施设备.某中学建立“网红”气膜体育馆（图1），气膜体育馆具有现代感、美观、大气、舒适、环保的特点，深受学生和教师的喜爱.气膜体育馆从某个角度看，可以近似抽象为半椭球面形状，该体育馆设计图纸比例（长度比）为1∶20（单位：m），图纸中半椭球面的方程为 $\frac{x^{2}}{4} + \frac{y^{2}}{4} + z^{2} = 1$ （ $(z ⩾ 0$ ）（如图2），则该气膜体育馆占地面积为（）

A、1000 $π$ m² B、540 $π$ m² C、2000 $π$ m² D、1600 $π$ m²

查看试题解析
6. 已知正实数x，y，则“ $x + y = 1$ ”是“ $\frac{1}{x} + \frac{1}{y} ⩾ 4$ ”的（）

A、必要不充分条件 B、充分不必要条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
7. 某旅游景区有如图所示A至H共8个停车位，现有2辆不同的白色车和2辆不同的黑色车，要求相同颜色的车不停在同一行也不停在同一列，则不同的停车方法总数为（）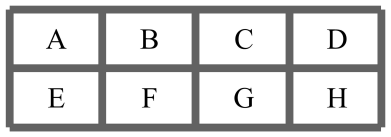

A、288 B、336 C、576 D、1680

查看试题解析
8. 已知偶函数 $f (x) = s i n (ω x + φ) - \sqrt{3} c o s (ω x + φ)$ （ $ω > 0$ ， $| φ | < \frac{π}{2}$ ）在 $(0 ， 1)$ 上恰有2个极大值点，则实数 $ω$ 的取值范围为（）

A、 $(2 π ， 4 π]$ B、 $(3 π ， 4 π]$ C、 $(4 π ， 6 π]$ D、 $(3 π ， 5 π]$

查看试题解析

二、多选题

9. 设复数 $z = \frac{i (1 + 2 i)}{1 + i}$ ，则（）

A、z的虚部为 $\frac{3}{2}$ B、 $\bar{z} = - \frac{1}{2} + \frac{3}{2} i$ C、 $| z | = \frac{\sqrt{10}}{2}$ D、 $z^{3} = 1$

查看试题解析
10. 已知圆M： $(x - 4)^{2} + (y - 5)^{2} = 12$ ，直线l： $m x - y - 2 m + 3 = 0$ ，直线l与圆M交于A，C两点，则下列说法正确的是（）

A、直线l恒过定点 $(2 ， 3)$ B、 $| \vec{A C} |$ 的最小值为4 C、 $\vec{M A} \cdot \vec{M C}$ 的取值范围为 $[- 12 ， 4]$ D、当 $∠ A M C$ 最小时，其余弦值为 $\frac{1}{2}$

查看试题解析
11. 高斯是德国著名数学家，近代数学奠基者之一，享有“数学王子”的称号，他和阿基米德，牛顿并列为世界三大数学家，用 $[x]$ 表示不超过x的最大整数，则 $y = [x]$ 称为高斯函数，例如 $[- 2.1] = - 3$ ， $[2.1] = 2$ .则下列说法正确的是（）

A、函数 $y = x - [x]$ 在区间 $[k ， k + 1)$ （ $k \in Z$ ）上单调递增 B、若函数 $f (x) = \frac{s i n x}{e^{x} - e^{- x}}$ ，则 $y = [f (x)]$ 的值域为 ${0}$ C、若函数 $f (x) = | \sqrt{1 + s i n 2 x} - \sqrt{1 - s i n 2 x} |$ ，则 $y = [f (x)]$ 的值域为 ${0 ， 1}$ D、 $x \in R$ ， $x \geq [x] + 1$

查看试题解析
12. 已知正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的棱长为2（如图所示），点M为线段 $C C_{1}$ （含端点）上的动点，由点A， $D_{1}$ ， M确定的平面为 $α$ ，则下列说法正确的是（）

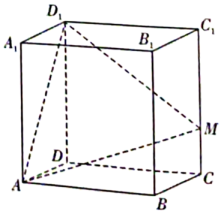A、平面 $α$ 截正方体的截面始终为四边形 B、点M运动过程中，三棱锥 $A_{1} - A D_{1} M$ 的体积为定值 C、平面 $α$ 截正方体的截面面积的最大值为 $4 \sqrt{2}$ D、三棱锥 $A_{1} - A D_{1} M$ 的外接球表面积的取值范围为 $[\frac{41}{4} π ， 12 π]$

查看试题解析

三、填空题

13. 已知 $| \vec{a} | = 3$ ， $| \vec{b} | = 2$ ， $\vec{a} \cdot \vec{b} = 1$ ，则 $| \vec{a} + \vec{b} | =$ .

查看试题解析
14. 已知函数 $f (x) = f^{'} (0) e^{2 x} - e^{- x}$ ，则 $f (0) =$ .

查看试题解析
15. 奥运古祥物“雪容融”是根据中国传统文化中灯笼的造型创作而成，现挂有如图所示的两串灯笼，每次随机选取其中一串并摘下其最下方的一个灯笼，直至某一串灯笼被摘完为止，则左边灯笼先摘完的概率为.

查看试题解析
16. 已知 $F_{1}$ ， $F_{2}$ ，是双曲线C： $\frac{x^{2}}{3} - \frac{y^{2}}{b^{2}} = 1$ 的左右焦点，过 $F_{1}$ 的直线与双曲线左支交于点A，与右支交于点B， $△ A F_{1} F_{2}$ 与 $△ B F_{1} F_{2}$ 内切圆的圆心分别为 $I_{1}$ ， $I_{2}$ ，半径分别为 $r_{1}$ ， $r_{2}$ ，则 $I_{1}$ 的横坐标为；若 $r_{1} ： r_{2} = 1 ： 3$ ，则双曲线离心率为.

查看试题解析

四、解答题

17. 记正项数列 ${a_{n}}$ 的前n项和为 $S_{n}$ ，且满足对任意正整数n有 $a_{n}^{2}$ ， $S_{n}$ ， $a_{n}$ 构成等差数列；等比数列 ${b_{n}}$ 的公比 $q > 1$ ， $b_{1} = a_{1}$ ， $b_{2} b_{6} = 64$ .

(1)、求 ${a_{n}}$ 和 ${b_{n}}$ 的通项公式；

(2)、设 $c_{n} = \frac{(3 n - 2) b_{n}}{n (n + 2)}$ ，求数列 ${c_{n}}$ 的前n项和 $T_{n}$ .

查看试题解析
18. 如图，在三棱锥 $P - A B C$ 中，平面 $P A C ⊥$ 平面 $A B C$ ， $P A = P C = 4$ ， $A B ⊥ B C$ ， D，E分别为 $P C$ ， $A C$ 中点，且 $B D ⊥ A C$ .

(1)、求 $\frac{A B}{B C}$ 的值；

(2)、若 $A C = 4$ ，求二面角 $E - B D - C$ 的余弦值.

查看试题解析
19. 如图，在平面四边形 $A B C D$ 中， $∠ B C D = \frac{π}{2}$ ， $A B = 1$ ， $∠ A B C = \frac{3 π}{4}$ .

(1)、当 $B C = \sqrt{2}$ ， $C D = \sqrt{7}$ 时，求 $△ A C D$ 的面积；

(2)、当 $∠ A D C = \frac{π}{6}$ ， $A D = 2$ 时，求 $c o s ∠ A C D$ .

查看试题解析
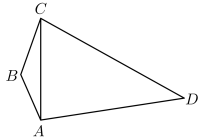20. 某社区拟对该社区内8000人进行核酸检测，现有以下两种核酸检测方案：
方案一：4人一组，采样混合后进行检测；
方案二：2人一组，采样混合后进行检测；
若混合样本检测结果呈阳性，则对该组所有样本全部进行单个检测；若混合样本检测结果呈阴性，则不再检测.

(1)、某家庭有6人，在采取方案一检测时，随机选2人与另外2名邻居组成一组，余下4人组成一组，求该家庭6人中甲，乙两人被分在同一组的概率；

(2)、假设每个人核酸检测呈阳性的概率都是0.01，每个人核酸检测结果相互独立，分别求该社区选择上述两种检测方案的检测次数的数学期望.以较少检测次数为依据，你建议选择哪种方案？
（附： $0.9 9^{2} \approx 0.98$ ， $0.9 9^{4} \approx 0.96$ ）

查看试题解析
21. 函数 $f (x) = a^{x} + 2 b x + e^{2}$ ，其中a，b为实数，且 $a \in (0 ， 1)$ .
（注 $e = 2.71828 ⋯$ 为自然对数的底数）

(1)、讨论 $f (x)$ 的单调性；

(2)、已知对任意 $b > 4 e^{2}$ ，函数 $f (x)$ 有两个不同零点，求a的取值范围.

查看试题解析
22. 已知点 $M (- 1 ， 1)$ 在抛物线E： $y^{2} = 2 p x$ （ $p > 0$ ）的准线上，过点M作直线 $l_{1}$ 与抛物线E交于A，B两点，斜率为2的直线 $l_{2}$ 与抛物线E交于A，C两点.

(1)、求抛物线E的标准方程；

(2)、（ⅰ）求证：直线 $B C$ 过定点；
（ⅱ）记（ⅰ）中的定点为H，设 $△ A B H$ 的面积为S，且满足 $S ⩽ 5$ ，求直线 $l_{1}$ 的斜率的取值范围.

查看试题解析