湖北省武汉市硚口区2022届高三下学期数学5月训练试卷

试卷更新日期：2022-06-24 类型：高考模拟

进入出卷网下载

一、单选题

1. 设集合 $A = {x | - 2 < x \leq 2 ， x \in Z}$ ， $B = {x | x^{2} \leq 1}$ ，则 $A ∩ B =$ （）

A、 ${- 1 ， 1}$ B、 $[- 1 ， 1]$ C、 ${- 1 ， 0 ， 1}$ D、 $[- 1 ， 0]$

查看试题解析
2. 欧拉恒等式 $e^{i π} + 1 = 0$ （ $i$ 为虚数单位， $e$ 为自然对数的底数）被称为数学中最奇妙的公式.它是复分析中欧拉公式 $e^{i π} = c o s x + i s i n x$ 的特例：当自变量 $x = π$ 时， $e^{i π} = c o s π + i s i n π = - 1$ ，得 $e^{i π} + 1 = 0$ .根据欧拉公式，复数 $e^{i \frac{5 π}{4}}$ 在复平面上所对应的点在第（）象限.

A、一 B、二 C、三 D、四

查看试题解析
3. ${(1 + x)}^{2} + {(1 + x)}^{3} + \dots + {(1 + x)}^{9}$ 的展开式中 $x^{2}$ 的系数是（）

A、60 B、80 C、84 D、120

查看试题解析
4. 函数 $y = (1 - \frac{2}{1 + e^{s i n x}}) | x |$ 的图象可能是（）

A、 B、 C、 D、

查看试题解析
5. 在南方不少地区，经常看到一种用木片、竹篾或苇蒿等材料制作的斗笠，用来遮阳或避雨，有一种外形为圆锥形的斗笠，称为“灯罩斗笠”，不同型号的斗笠大小经常用帽坡长（母线长）和帽底宽（底面圆直径长）两个指标进行衡量，现有一个“灯罩斗笠”，帽坡长20厘米，帽底宽 $20 \sqrt{3}$ 厘米，关于此斗笠，下列说法不正确的是（）

A、斗笠轴截面（过顶点和底面中心的截面图形）的顶角为120° B、过斗笠顶点和斗笠侧面上任意两母线的截面三角形的最大面积为 $100 \sqrt{3}$ 平方厘米 C、若此斗笠顶点和底面圆上所有点都在同一个球上，则该球的表面积为 $1600 π$ 平方厘米 D、此斗笠放在平面上，可以完全盖住的球（保持斗笠不变形）的最大半径为 $20 \sqrt{3} - 30$ 厘米

查看试题解析
6. 抛物线有如下光学性质：由焦点射出的光线经抛物线反射后平行于抛物线的对称轴；反之，平行于抛物线对称轴的入射光线经抛物线反射后必经过抛物线的焦点．已知抛物线y²＝4x的焦点为F，一平行于x轴的光线从点M(3，1)射入，经过抛物线上的点A反射后，再经抛物线上的另一点B射出，则直线AB的斜率为（）

A、 $\frac{4}{3}$ B、－ $\frac{4}{3}$ C、± $\frac{4}{3}$ D、－ $\frac{16}{9}$

查看试题解析
7. 两不共线的向量 $\vec{a}$ ， $\vec{b}$ ，满足 $| \vec{a} | = 3 | \vec{b} |$ ，且 $\forall t \in R$ ， $| \vec{a} - t \vec{b} | \geq | \vec{a} - \vec{b} |$ ，则 $c o s ⟨ \vec{a} ， \vec{b} ⟩ =$ （）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{3}}{2}$ C、 $\frac{1}{3}$ D、 $\frac{\sqrt{3}}{3}$

查看试题解析
8. 函数 $f (x)$ ， $g (x)$ 的定义域都是 $D$ ，直线 $x = x_{0} (x_{0} \in D)$ 与 $y = f (x)$ ， $y = g (x)$ 的图象分别交于 $A$ ， $B$ 两点，若线段 $A B$ 的长度是不为 $0$ 的常数，则称曲线 $y = f (x)$ ， $y = g (x)$ 为“平行曲线”设 $f (x) = e^{x} - a l n x + c (a > 0 ， c \neq 0)$ ，且 $y = f (x)$ ， $y = g (x)$ 为区间 $(0 ， + ∞)$ 的“平行曲线”其中 $g (1) = e$ ， $g (x)$ 在区间 $(2 ， 3)$ 上的零点唯一，则 $a$ 的取值范围是（）

A、 $(\frac{e^{2}}{l n 3} ， \frac{e^{4}}{l n 2})$ B、 $(\frac{e^{2}}{l n 2} ， \frac{e^{3}}{l n 3})$ C、 $(\frac{e^{3}}{l n 3} ， \frac{2 e^{4}}{l n 2})$ D、 $(\frac{2 e^{3}}{l n 3} ， \frac{e^{4}}{l n 2})$

查看试题解析

二、多选题

9. 某高中学校积极响应国家“阳光体育运动”的号召，为确保学生每天一小时的体育锻炼，调查该校2000名高中学生每周平均参加体育锻炼时间的情况，现从高一、高二、高三三个年级学生中按照 $3 ： 1 ： 1$ 的比例分层抽样，收集了200名学生每周平均体育运动时间的样本数据（单位：小时），整理后得到如图所示的频率分布直方图，则下列说法中，正确的是（）

A、估计该校高中学生每周平均体育运动时间不足4小时的人数为500人 B、估计该校高中学生每周平均体育运动时间不少于8小时的人数百分比为20% C、估计该校高中学生每周平均体育运动时间的中位数为5小时 D、估计该校高中学生每周平均体育运动时间为5.8小时

查看试题解析
10. 甲乙两个质地均匀且完全一样的四面体，每个面都是正三角形，甲四个面上分别标有数字1，2，3，4，乙四个面上分别标有数字5，6，7，8，同时抛掷这两个四面体一次，记事件 $A$ 为“两个四面体朝下一面的数字之和为奇数”，事件 $B$ 为“甲四面体朝下一面的数字为奇数”，事件 $C$ 为“乙四面体朝下一面的数字为偶数”，则下列结论正确的是（）

A、 $P (A) = P (B) = P (C)$ B、 $P (B C) = P (A C) = P (A B)$ C、 $P (A B C) = \frac{1}{8}$ D、 $P (A) \cdot P (B) \cdot P (C) = \frac{1}{8}$

查看试题解析
11. 已知 $f (x) = 1 - 2 c o s^{2} (ω x + \frac{π}{3}) (ω > 0)$ ，则下列判断中，错误的是（）

A、若 $f (x_{1}) = 1$ ， $f (x_{2}) = - 1$ ，且 ${| x_{1} - x_{2} |}_{m i n} = π$ ，则 $ω = 2$ B、存在 $ω \in (0 ， 2)$ ，使得 $f (x)$ 的图像右移 $\frac{π}{6}$ 个单位长度后得到的图像关于 $y$ 轴对称 C、若 $f (x)$ 在 $[0 ， 2 π]$ 上恰有7个零点，则 $ω$ 的取值范围为 $[\frac{41}{24} ， \frac{47}{24}]$ D、若 $f (x)$ 在 $[- \frac{π}{6} ， \frac{π}{4}]$ 上单调递增，则 $ω$ 的取值范围为 $(0 ， \frac{2}{3}]$

查看试题解析
12. 已知数列 ${a_{n}}$ ， ${b_{n}}$ 均为递增数列，它们的前 $n$ 项和分别为 $S_{n}$ ， $T_{n}$ ，且满足 $a_{n} + a_{n + 1} = 2 n$ ， $b_{n} \cdot b_{n + 1} = 2^{n}$ ，则下列结论正确的是（）

A、 $0 < a_{1} < 1$ B、 $S_{2 n} = n^{2} + 3 n - 2$ C、 $1 < b_{1} < \sqrt{2}$ D、 $S_{2 n} < T_{2 n}$

查看试题解析

三、填空题

13. 如果 $x_{1}$ ， $x_{2}$ ， $x_{3}$ ， $x_{4}$ 的方差是 $\frac{1}{3}$ ，则 $3 x_{1}$ ， $3 x_{2}$ ， $3 x_{3}$ ， $3 x_{4}$ 的方差为.

查看试题解析
14. 若 $f (x) = a s i n (x + \frac{π}{4}) + b s i n (x - \frac{π}{4}) (a b \neq 0)$ 是偶函数，则有序实数对( $a ， b$ )可以
是.

查看试题解析
15. 双曲线C： $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 与抛物线y²=8x有共同的焦点 $F_{2}$ ，双曲线左焦点为 $F_{1}$ ，点P是双曲线右支一点，过 $F_{1}$ 向 $∠ F_{1} P F_{2}$ 的角平分线做垂线，垂足为N， $| O N | =$ 1，则双曲线的离心率是.

查看试题解析
16. 如图，多面体ABCDEF中，面ABCD为正方形，DE⊥平面ABCD，CF∥DE，且AB=DE=2，CF=1，G为棱BC的中点，H为棱DE上的动点，有下列结论：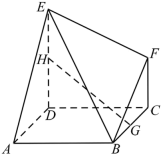
①当H为DE的中点时，GH∥平面ABE；
②存在点H，使得GH⊥AE；
③三棱锥B−GHF的体积为定值；
④三棱锥E−BCF的外接球的表面积为 $14 π$ ．
其中正确的结论序号为．（填写所有正确结论的序号）

查看试题解析

四、解答题

17. 在三角形中，∠A、∠B、∠C分别对应的边为a，b，c，且满足关系式为： $tan A + tan B + tan C = \frac{\sqrt{3}}{3} tan A tan B ．$

(1)、求∠C的的大小；

(2)、若c=2，求 $a^{2} + b^{2}$ 的取值范围

查看试题解析
18. 已知数列 ${a_{n}}$ 满足： $a_{1} = 1$ ，且 $a_{n + 1} - 2 a_{n} = 0$ ，等差数列 ${b_{n}}$ 满足： $b_{1} = 2$ ， $b_{5} + b_{7} = 34$ ，令 $c_{n} = a_{n} - b_{n}$ ，（ $n \in N^{*}$ ）.

(1)、求数列 ${c_{n}}$ 的通项公式；

(2)、求数列 ${| c_{n} |}$ 的前n项和 $S_{n}$ .

查看试题解析
19. 新型冠状病毒的传染性是非常强的，而且可以通过接触传播或者是呼吸道飞沫传播，感染人群年龄大多数是40岁以上的人群.该病毒进入人体后有潜伏期，并且潜伏期越长，感染他人的可能性越高，现对100个病例的潜伏期（单位：天）进行调查，统计发现潜伏期中位数为5，平均数为7.21，方差为5.08.如果认为超过8天的潜伏期属于“长潜伏期”.按照年龄统计样本得到下面的列联表：

长潜伏期

非长潜伏期

40岁以上

15

55

40岁及以下

10

20

附： $K^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ .

$K^{2} \geq k$

0.1

0.05

$k$

2.706

3.841

若随机变量 $Z$ 服从正态分布 $N (μ, σ^{2})$ ，则 $P (μ - σ < Z < μ + σ) = 0.6826$ ， $P (μ - 2 σ < Z < μ + 2 σ) = 0.9544$ ， $P (μ - 3 σ < Z < μ + 3 σ) = 0.9974$ ， $\sqrt{5.08} \approx 2.25$ .

(1)、能否有90%以上的把握认为“长潜伏期”与年龄有关；

(2)、假设潜伏期 $Z$ 服从正态分布 $N (μ, σ^{2})$ ，其中 $μ$ 近似为样本平均数， $σ^{2}$ 近似为样本方差，现在很多省份对入境旅客一律要求隔离14天，请用概率的知识解释其合理性；

(3)、以题目中的样本频率估计概率，并计算4个病例中有 $X (X \in N *)$ 个进入“长潜伏期”的期望与方差.

查看试题解析
20. 如图，四棱锥 $P - A B C D$ 中，底面 $A B C D$ 是直角梯形， $A D ⊥ D C$ ， $A D ∥ B C$ ，平面 $P C D ⊥$ 平面 $A B C D$ ，设平面 $P A D$ 与平面 $P B C$ 的交线为 $l$ .

(1)、证明： $l ⊥$ 平面 $P C D$ ；

(2)、已知 $A D = P D = D C = \frac{1}{2} B C = 2$ ，且 $∠ D P C = 30 °$ ，求直线 $P B$ 与平面 $P A D$ 所成角的正弦值.

查看试题解析
21. 已知 $P$ 是平面上的动点，且点 $P$ 与 $F_{1} (- 1 ， 0) 、 F_{2} (1 ， 0)$ 的距离之和为 $2 \sqrt{3}$ ．点 $P$ 的轨迹为曲线 $E$ ．

(1)、求动点 $P$ 的轨迹 $E$ 的方程；

(2)、不与 $y$ 轴垂直的直线 $l$ 过点 $F_{1}$ 且交曲线 $E$ 于 $M ， N$ 两点，曲线 $E$ 与 $x$ 轴的交点为 $A ， B$ ，当 $| M N | \geq \frac{8}{5} \sqrt{3}$ 时，求 $\vec{A M} \cdot \vec{N B} + \vec{A N} \cdot \vec{M B}$ 的取值范围．

查看试题解析
22. 已知函数 $f (x) = a x^{2} + l n (x + 1)$ ．
（Ⅰ）当 $a = - \frac{1}{4}$ 时，求函数 $f (x)$ 的单调区间；
（Ⅱ）当 $x \in [0 ， + \infty)$ 时，不等式 $f (x) \leq x$ 恒成立，求实数 $a$ 的取值范围．
（Ⅲ）求证： $(1 + \frac{2}{2 \times 3}) (1 + \frac{4}{3 \times 5}) (1 + \frac{8}{5 \times 9}) \cdot ┄ \cdot [1 + \frac{2^{n}}{(2^{n - 1} + 1) (2^{n} + 1)}] < e$ （ $n \in N^{*}$ ， $e$ 是自然对数的底数）.

查看试题解析

	长潜伏期	非长潜伏期
40岁以上	15	55
40岁及以下	10	20

$K^{2} \geq k$	0.1	0.05
$k$	2.706	3.841