湖北省省级示范高中2022届高三下学期数学5月模拟考试试卷

试卷更新日期：2022-06-24 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知集合 $A = {x | x^{2} - 2 x > 0}$ ， $B = {x | x > a}$ ，若 $A ∪ B = R$ ，则实数 $a$ 的取值范围是（）

A、 $(- ∞ ， 0)$ B、 $(- \infty ， 0]$ C、 $(2 ， + ∞)$ D、 $[2 ， + \infty)$

查看试题解析
2. 已知复数 $z_{1}$ ， $z_{2}$ ，则下面四个命题中为真命题的是（）
$P_{1}$ ：若 $| z_{1} | = | z_{2} |$ ，则 $z_{1} = z_{2}$ ； $P_{2}$ ：若 $z_{1} = - z_{2}$ ，则 $| z_{1} | = | - z_{2} |$ ；
$P_{3}$ ：若 $z_{1} = \bar{z_{2}}$ ，则 $| z_{1} | = | z_{2} |$ ； $P_{4}$ ：若 $| z_{1} | = | z_{2} |$ ，则 $z_{1} = \bar{z_{2}}$ .

A、 $P_{1}$ ， $P_{3}$ B、 $P_{1}$ ， $P_{4}$ C、 $P_{2}$ ， $P_{3}$ D、 $P_{2}$ ， $P_{4}$

查看试题解析
3. 若角 $α$ 的终边经过点 $P (1 ， - 2)$ ，则 $s i n α$ 的值为（）

A、 $\frac{2 \sqrt{5}}{5}$ B、 $\frac{\sqrt{5}}{5}$ C、 $- \frac{\sqrt{5}}{5}$ D、 $- \frac{2 \sqrt{5}}{5}$

查看试题解析
4. 已知非零向量 $\overset{⇀}{a}$ ， $\overset{⇀}{b}$ ， $\overset{⇀}{c}$ ，那么“ $\overset{⇀}{a} = \overset{⇀}{b}$ ”是“ $\overset{⇀}{a} \cdot \overset{⇀}{c} = \overset{⇀}{b} \cdot \overset{⇀}{c}$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
5. 已知 $△ A B C$ 中， $A B = 4$ ， $B C = 3$ ， $A C = 5$ ，以 $A C$ 为轴旋转一周得到一个旋转体，则该旋转体的内切球的表面积为（）

A、 $\frac{49}{36} π$ B、 $\frac{576}{49} π$ C、 $\frac{576}{25} π$ D、 $\frac{345}{25} π$

查看试题解析
6. 2022国家号召全民健身口号中提到：“儿童健身，天真活泼；青年健身，朝气蓬勃.”提倡学生走向操场、走进大自然、走到阳光下.为弘扬运动精神，潜江中学特地每天开展课外文体活动.学校操场可供2000名学生运动，每周四有踢毽子、《本草纲目》健身操两种运动可供选择，经过调查发现，凡是这周选踢毽子的，下周会有30%的改选健身操；而选健身操的，下周会20%改选踢毽子.用 $a_{n} ， b_{n}$ 分别表示在第 $n$ 周选踢毽子的和健身操的人数，如果 $b_{1} = 1200$ ，且 $a_{n} + b_{n} = 2000$ ，则 $b_{11}$ 为（）

A、800 B、1000 C、1200 D、1400

查看试题解析
7. 椭圆： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 有一特殊性质，从一个焦点射出的光线到达椭圆上的一点 $P$ 反射后，经过另一个焦点.已知椭圆的焦距为2，且 $| P F_{1} | + | P F_{2} | = 4$ ，当 $s i n ∠ F_{1} P F_{2} = \frac{1}{2}$ 时，椭圆的中心 $O$ 到与椭圆切于点 $P$ 的切线的距离为：（）

A、1 B、 $\frac{\sqrt{6} + \sqrt{2}}{4}$ C、 $\frac{\sqrt{6} + \sqrt{2}}{2}$ D、 $\frac{\sqrt{6} + \sqrt{2}}{2}$ 或 $\frac{\sqrt{6} - \sqrt{2}}{2}$

查看试题解析
8. 已知： $a = e^{0.42}$ ， $b = 2^{0.5}$ ， $c = l o g_{4} 5$ ，则 $a$ 、 $b$ 、 $c$ 大小关系为（）

A、 $b > a > c$ B、 $a > b > c$ C、 $c > a > b$ D、 $b > c > a$

查看试题解析

二、多选题

9. 截止5月6日，全球不明原因儿童肝炎超300例.在对前期169例病例的研究发现，74例腺病毒检测阳性.其中20例新冠病毒检测阳性，19例腺病毒和新冠病毒均呈阳性，现从前期病例中随机抽取2例，记事件 $M$ 为“恰有1例新冠病毒阳性”，事件 $N$ 为“恰有1例腺病毒和新冠病毒均呈阳性”，下列说法错误的有：（）

A、事件 $M$ 的对立事件为“至多有1例新冠病毒阳性” B、 $P (N | M) = \frac{19}{20}$ C、事件 $M$ 与事件 $N$ 为互斥事件 D、事件 $M$ 与事件 $N$ 为独立事件

查看试题解析
10. 已知 $f (x) = s i n x + a c o s x (a \neq 0)$ ，下列说法正确的有（）

A、若 $f (x)$ 过点 $(- \frac{π}{6} ， 1)$ ，则 $a = \pm \sqrt{3}$ B、若 $f (x)$ 在 $y$ 侧右侧的第一条对称轴为 $x = \frac{π}{4}$ ，则 $a = 1$ C、当 $a > 0$ 时， $f (x)$ 在 $[- \frac{π}{2} ， 0]$ 单调递增 D、将 $g (x) = f (x) + x c o s x$ 的正零点按从小到大的顺序排列构成数列 ${x_{n}}$ ，若 $t a n x_{1} + t a n x_{3} = 0$ ，则 $a = - π$

查看试题解析
11. 正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的棱长为3， $M$ 、 $N$ 为底面A₁B₁C₁D₁内的动点，且 $\vec{A M} = \vec{A A_{1}} + λ (\vec{A_{1} B_{1}} + \vec{A_{1} D_{1}}) (λ \in [0 ， 1])$ ，直线 $B N$ 与 $C C_{1}$ 所成角为 $30 °$ ，下列说法正确的是（）

A、动点 $N$ 轨迹长度为 $\sqrt{3}$ B、 $C M ⊥ B D$ C、线段 $M N$ 的长度最小值为 $\frac{3}{2} \sqrt{2} - \sqrt{3}$ D、三棱锥 $B - A_{1} M N$ 的体积可以取值为3

查看试题解析
12. 函数 $f (x)$ 满足 $a > 0$ ， $b > 0$ ，函数 $g (x) = \frac{f (x)}{e^{x}}$ 的一个零点也是其本身的极值点，则 $f (x)$ 可能的表达式有（）

A、 $a x^{3} + b x + 1$ B、 $a x - b l n x$ C、 $a s i n x + b c o s x + 1$ D、 $a x^{2} + b x + 1$

查看试题解析

三、填空题

13. 北京时间2022年4月16日9时56分，神舟十三号载人飞船返回舱在东风着陆场成功着陆.东风着陆场着陆面积达到了2万平方公里，相当于内蒙古四子王旗航天着陆场着陆面积的10倍，主着陆场正常的着陆范围是 $60 k m \times 60 k m$ 的区域.在神舟十三号着陆前，航天科学家们经过了无数次的电子模拟，发现飞船着陆点离标志观察点 $A$ 的距离 $X k m$ 满足 $X ~ N (μ ， σ^{2})$ .下图是 $X$ 经过100次模拟实验中的频率分布直方图. $μ$ 可以用图中 $X$ 的平均值代替， $σ = t - 35$ ，其中 $t$ 是图中的中位数的估计值（每组数据用这一组的中点值代替），则 $P (37 < x \leq 42)$ $P (40 < x \leq 45)$ （用“ $>$ ， $<$ ， $=$ ”之一填入）

查看试题解析
14. 已知圆 $O$ ： $x^{2} + y^{2} = 3$ ， $l$ 为过 $M (1 ， \sqrt{2})$ 的圆的切线， $A$ 为 $l$ 上任一点，过 $A$ 作圆 $N$ ： ${(x + 2)}^{2} + y^{2} = 4$ 的切线，则切线长的最小值是.

查看试题解析
15. 已知 ${a_{n}}$ 为等比数列，且 $a_{n} > 0$ ， $a_{1} + a_{2} = 1$ ， $a_{3} + a_{4} = 9$ ， $T_{n}$ 为其前 $n$ 项之积，若 $T_{n} > 1$ ，则 $n$ 的最小值为.

查看试题解析
16. 已知 $0 < a \neq 1$ ， $a^{x} > l o g_{a}^{} x (x > 0)$ 恒成立，则 $a$ 的取值范围为.

查看试题解析

四、解答题

17. 已知数列 ${a_{n}}$ 前 $n$ 项和 $S_{n} = \frac{3 n^{2} + n}{2}$ ， ${b_{n}}$ 的前 $n$ 项之积 $T_{n} = 2^{\frac{n (n + 1)}{2}} (n \in N^{*})$ .

(1)、求 ${a_{n}}$ 与 ${b_{n}}$ 的通项公式.

(2)、把数列 ${a_{n}}$ 和 ${b_{n}}$ 的公共项由小到大排成的数列为 ${c_{n}}$ ，求 $c_{1} + c_{2} + \cdot \cdot \cdot + c_{20}$ 的值.

查看试题解析
18. 在 $△ A B C$ 中，若 $2 S_{△ A B C} = \sqrt{3} \vec{B A} \cdot \vec{B C}$ .

(1)、求 $∠ B$ 的值；

(2)、如图，若 $A B = A C$ ， $D$ 为 $△ A B C$ 外一点，且 $D A = \sqrt{3}$ ， $D C = 2$ ， $∠ A D C = θ$ ，求 $S_{四边形 A B C D}$ 的最大值及相应的 $θ$ .

查看试题解析
19. 如图，在直角梯形 $A B C D$ 中， $∠ B A D = 90 °$ ， $∠ A D C = 45 °$ ， $A D = 3 = P B + B A$ ， $B C ∥ A D$ ， $P A ⊥$ 平面 $A B C D$ ， $E$ ， $F$ 分别是 $A B$ ， $C P$ 的中点.

(1)、证明： $E F ∥$ 平面 $P A D$ ；

(2)、若二面角 $P - C D - E$ 的正弦值等于 $\frac{\sqrt{10}}{5}$ ，求四棱锥 $P - A B C D$ 的体积.

查看试题解析
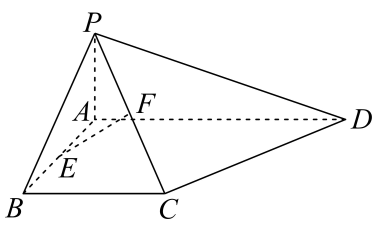20. 某校高三年级非常重视学生课余时间的管理，进入高三以来，倡导学生利用中午午休前40分钟，晚餐后30分钟各做一套试卷.小红、小明两位同学都选择做数学或物理试卷，对2位同学过去100天的安排统计如下：
科目选择（中午，
晚上）
（数，数）
（数，物）
（物，数）
（物，物）
休息
小红
25天
20天
35天
10天
10天
小明
20天
25天
15天
30天
10天
假设小红、小明选择科目相互独立，用频率估计概率：

(1)、请预测在今后的5天中小红恰有 $3$ 天中午和晚上都选数学的概率；

(2)、记 $X$ 为两位同学在一天中选择科目的个数，求 $X$ 的分布列和数学期望 $E (X)$ ；

(3)、试判断小红、小明在晚上做物理试卷的条件下，哪位同学更有可能中午选择做数学试卷，并说明理由.

查看试题解析
21. 已知椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的右顶点为A，O为坐标原点，且椭圆C的离心率为 $\frac{\sqrt{3}}{2}$ ， P，Q为椭圆上两点，当QO＝QA时， $△ O Q A$ 的面积为 $\frac{\sqrt{3}}{2}$ ．

(1)、求椭圆C的标准方程．

(2)、过点P任作倾斜角互补的两条直线 $l_{1}$ ， $l_{2}$ ，分别与椭圆C交于M，N两点，是否存在点P，使得AP⊥MN恒成立？若存在，求出所有满足条件的点P；若不存在，请说明理由．

查看试题解析
22. 已知函数 $f (x) = x \cdot l n x + \frac{1}{e}$ .

(1)、求 $f (x)$ 的单调区间与最小值.

(2)、求证： $e^{\frac{x}{2}} + l n x > c o s 2 x + \frac{s i n x - 1}{x}$ .

查看试题解析