湖南省怀化市2022年中考数学试卷

试卷更新日期：2022-06-23 类型：中考真卷

进入出卷网下载

一、单选题

1. $- \frac{1}{2}$ 的相反数是（）

A、-2 B、2 C、 $- \frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
2. 代数式 $\frac{2}{5}$ x， $\frac{1}{π}$ ， $\frac{2}{x^{2} + 4}$ ， x²﹣ $\frac{2}{3}$ ， $\frac{1}{x}$ ， $\frac{x + 1}{x + 2}$ 中，属于分式的有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
3. 2022年3月11日，新华社发文总结2021年中国取得的科技成就，其中包括“奋斗者”号载人潜水器最深下潜至10909米.其中数据10909用科学记数法表示为（）

A、10.909×10² B、1.0909×10³ C、0.10909×10⁴ D、1.0909×10⁴

查看试题解析
4. 下列说法正确的是（）

A、相等的角是对顶角 B、对角线相等的四边形是矩形 C、三角形的外心是它的三条角平分线的交点 D、线段垂直平分线上的点到线段两端的距离相等

查看试题解析
5. 下列计算正确的是（）

A、（2a²）³＝6a⁶ B、a⁸÷a²＝a⁴ C、 $\sqrt{(- 2)^{2}}$ ＝2 D、（x﹣y）²＝x²﹣y²

查看试题解析
6. 下列一元二次方程有实数解的是（）

A、2x²﹣x+1＝0 B、x²﹣2x+2＝0 C、x²+3x﹣2＝0 D、x²+2＝0

查看试题解析
7. 一个多边形的内角和为900°，则这个多边形是（）

A、七边形 B、八边形 C、九边形 D、十边形

查看试题解析
8. 如图，△ABC沿BC方向平移后的像为△DEF，已知BC=5，EC=2，则平移的距离是（）

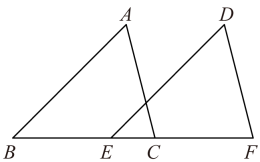A、1 B、2 C、3 D、4

查看试题解析
9. 从下列一组数﹣2，π，﹣ $\frac{1}{2}$ ， ﹣0.12，0，﹣ $\sqrt{5}$ 中随机抽取一个数，这个数是负数的概率为（）

A、 $\frac{5}{6}$ B、 $\frac{2}{3}$ C、 $\frac{1}{2}$ D、 $\frac{1}{3}$

查看试题解析
10. 如图，直线AB交x轴于点C，交反比例函数y＝ $\frac{a - 1}{x}$ （a＞1）的图象于A、B两点，过点B作BD⊥y轴，垂足为点D，若S_△BCD＝5，则a的值为（）

A、8 B、9 C、10 D、11

查看试题解析

二、填空题

11. 计算 $\frac{x + 5}{x + 2}$ ﹣ $\frac{3}{x + 2}$ ＝.

查看试题解析
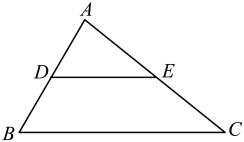
12. 因式分解： $x^{2} - x^{4} =$ .

查看试题解析
13. 已知点A（﹣2，b）与点B（a，3）关于原点对称，则a﹣b =.

查看试题解析
14. 如图，△ABC中，点D、E分别是AB、AC的中点，若S_△ADE＝2，则S_△ABC＝.

查看试题解析
15. 如图，AB与⊙O相切于点C，AO=3，⊙O的半径为2，则AC的长为.

查看试题解析
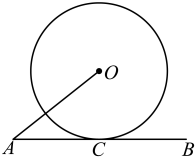16. 正偶数2，4，6，8，10，…，按如下规律排列，
则第27行的第21个数是 .

查看试题解析

三、解答题

17. 计算：（3.14﹣π）⁰+| $\sqrt{2}$ ﹣1|+（ $\frac{1}{2}$ ）^﹣¹﹣ $\sqrt{8}$ .

查看试题解析
18. 解不等式组，并把解集在数轴上表示出来.
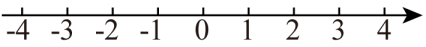${\begin{array}{l} 5 x - 1 > 3 (x + 1) ① \\ 3 x - 2 \leq 2 x + 1 ② \end{array}$

查看试题解析
19. 某地修建了一座以“讲好隆平故事，厚植种子情怀”为主题的半径为800米的圆形纪念园.如图，纪念园中心点A位于C村西南方向和B村南偏东60°方向上，C村在B村的正东方向且两村相距2.4千米.有关部门计划在B、C两村之间修一条笔直的公路来连接两村.问该公路是否穿过纪念园？试通过计算加以说明. （参考数据： $\sqrt{3}$ ≈1.73， $\sqrt{2}$ ≈1.41）

查看试题解析
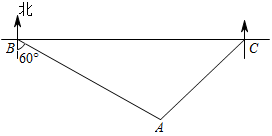20. 如图，点A，B，C，D在⊙O上， $\overset{⌢}{A B}$ ＝ $\overset{⌢}{C D}$ .求证：

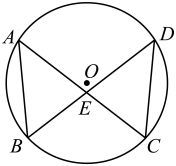(1)、AC＝BD；

(2)、△ABE∽△DCE.

查看试题解析
21. 电视剧《一代洪商》在中央电视台第八套播出后，怀化市各旅游景点知名度得到显菩提高.为全面提高旅游服务质量，旅游管理部门随机抽取了100名游客进行满意度调查，并绘制成如下不完整的频数分布表和扇形统计图.
频数分布表
满意程度
频数（人）
频率
非常满意
50
0.5
满意
30
0.3
一般
a
c
不满意
b
0.05
合计
100
1
根据统计图表提供的信息，解答下列问题：

(1)、a＝， b＝， c＝；

(2)、求扇形统计图中表示“一般”的扇形圆心角α的度数；

(3)、根据调查情况，请你对各景点的服务提一至两条合理建议.

查看试题解析
22. 如图，在等边三角形ABC中，点M为AB边上任意一点，延长BC至点N，使CN=AM，连接MN交AC于点P，MH⊥AC于点H.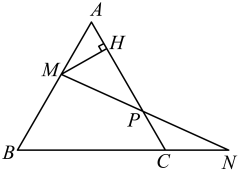

(1)、求证：MP=NP；

(2)、若AB＝a，求线段PH的长（结果用含a的代数式表示）.

查看试题解析
23. 去年防洪期间，某部门从超市购买了一批数量相等的雨衣（单位：件）和雨鞋（单位：双），其中购买雨衣用了400元，购买雨鞋用了350元，已知每件雨衣比每双雨鞋贵5元.

(1)、求每件雨衣和每双雨鞋各多少元？

(2)、为支持今年防洪工作，该超市今年的雨衣和雨鞋单价在去年的基础上均下降了20%，并按套（即一件雨衣和一双雨鞋为一套）优惠销售. 优惠方案为：若一次购买不超过5套，则每套打九折：若一次购买超过5套，则前5套打九折，超过部分每套打八折.设今年该部门购买了a套，购买费用为W元，请写出W关于a的函数关系式.

(3)、在（2）的情况下，今年该部门购买费用不超过320元时最多可购买多少套？

查看试题解析
24. 如图一所示，在平面直角坐标中，抛物线y＝ax²+2x+c经过点A(﹣1，0）、B（3，0），与y轴交于点C，顶点为点D.在线段CB上方的抛物线上有一动点P，过点P作PE⊥BC于点E，作PF $∥$ AB交BC于点F.

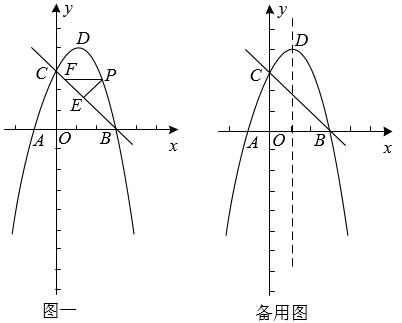(1)、求抛物线和直线BC的函数表达式，

(2)、当△PEF的周长为最大值时，求点P的坐标和△PEF的周长.

(3)、若点G是抛物线上的一个动点，点M是抛物线对称轴上的一个动点，是否存在以C、B、G、M为顶点的四边形为平行四边形？若存在，求出点G的坐标，若不存在，请说明理由.

查看试题解析

满意程度	频数（人）	频率
非常满意	50	0.5
满意	30	0.3
一般	a	c
不满意	b	0.05
合计	100	1