四川省雅安市2020-2021学年七年级下学期期末数学试卷
试卷更新日期:2022-06-22 类型:期末考试
一、单选题
-
1. 下列图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 计算(a2)3的结果为( )A、a4 B、a5 C、a6 D、a93. 用科学记数方法表示- , 得( )A、 B、 C、 D、-4. 某路口交通信号灯的时间设置为:红灯亮25秒,绿灯亮32秒,黄灯亮3秒.当人或车随机经过该路口时,遇到绿灯的概率为( )A、 B、 C、 D、5. 将一根长为 的铁丝制作成一个长方形,则这个长方形的长 与宽 之间的关系式为( )A、 B、 C、 D、6. 在三角形中,一定能将其面积分成相等两部分的是( )A、中线 B、高线 C、角平分线 D、某一边的垂直平分线7. 下列计算正确的是( )A、a2+a2=a4 B、a3•a2=a5 C、2(a﹣b)=2a﹣b D、(﹣b2)3=﹣b58. 如图,下列条件中不能判定a∥b的是( )
2. 计算(a2)3的结果为( )A、a4 B、a5 C、a6 D、a93. 用科学记数方法表示- , 得( )A、 B、 C、 D、-4. 某路口交通信号灯的时间设置为:红灯亮25秒,绿灯亮32秒,黄灯亮3秒.当人或车随机经过该路口时,遇到绿灯的概率为( )A、 B、 C、 D、5. 将一根长为 的铁丝制作成一个长方形,则这个长方形的长 与宽 之间的关系式为( )A、 B、 C、 D、6. 在三角形中,一定能将其面积分成相等两部分的是( )A、中线 B、高线 C、角平分线 D、某一边的垂直平分线7. 下列计算正确的是( )A、a2+a2=a4 B、a3•a2=a5 C、2(a﹣b)=2a﹣b D、(﹣b2)3=﹣b58. 如图,下列条件中不能判定a∥b的是( ) A、∠1=∠2 B、∠1=∠4 C、∠1+∠2=180° D、∠1+∠3=180°9. 根据下列已知条件,能唯一画出的是( )A、 , , B、 , C、 , , D、 , ,10. 下列各式中能用平方差公式计算的是( )A、 B、 C、 D、11. 在雨地里放置一个无盖的容器,如果雨水均匀地落入容器,容器内水面高度 与时间 的函数图象如图所示,那么这个容器的形状可能是( )
A、∠1=∠2 B、∠1=∠4 C、∠1+∠2=180° D、∠1+∠3=180°9. 根据下列已知条件,能唯一画出的是( )A、 , , B、 , C、 , , D、 , ,10. 下列各式中能用平方差公式计算的是( )A、 B、 C、 D、11. 在雨地里放置一个无盖的容器,如果雨水均匀地落入容器,容器内水面高度 与时间 的函数图象如图所示,那么这个容器的形状可能是( ) A、
A、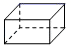 B、
B、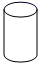 C、
C、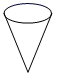 D、
D、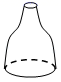 12. 如图,在Rt△ABC中,∠CBA=90°,∠CAB的角平分线AP和∠MCB的平分线CF相交于点D,AD交CB于点P,CF交AB的延长线于点F,过点D作DE⊥CF交CB的延长线于点G,交AB的延长线于点E,连接CE并延长交FG于点H,则下列结论:①∠CDA=45°;②AF﹣CG=CA;③DE=DC;④CF=2CD+EG;其中正确的有( )
12. 如图,在Rt△ABC中,∠CBA=90°,∠CAB的角平分线AP和∠MCB的平分线CF相交于点D,AD交CB于点P,CF交AB的延长线于点F,过点D作DE⊥CF交CB的延长线于点G,交AB的延长线于点E,连接CE并延长交FG于点H,则下列结论:①∠CDA=45°;②AF﹣CG=CA;③DE=DC;④CF=2CD+EG;其中正确的有( )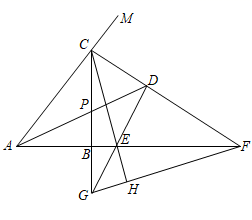 A、②③ B、②④ C、①②③④ D、①③④
A、②③ B、②④ C、①②③④ D、①③④二、填空题
-
13. 已知一个角的补角是这个角的余角的3倍,则这个角是度.14. 如果4x2+ax+9是一个完全平方式,那么a的值为.15. 如图,△ABC≌△ADE,∠B=70°,∠C=30°,∠DAC=20°,则∠EAC的度数为 .
 16. 如图,钝角三角形△ABC的面积是15,最长边AB=10,BD平分∠ABC , 点M , N分别是BD , BC上的动点,则CM+MN的最小值为
16. 如图,钝角三角形△ABC的面积是15,最长边AB=10,BD平分∠ABC , 点M , N分别是BD , BC上的动点,则CM+MN的最小值为 17. 已知 , 那么的值是 .18. 如图,在的正方形格纸中,有一个以格点为顶点的 , 请你找出格纸中所有与成轴对称且也以格点为顶点的三角形,这样的三角形共有个.
17. 已知 , 那么的值是 .18. 如图,在的正方形格纸中,有一个以格点为顶点的 , 请你找出格纸中所有与成轴对称且也以格点为顶点的三角形,这样的三角形共有个.
三、解答题
-
19.(1)、计算x•x3+(2x2)2﹣2x5÷x(2)、先化简,再求值:[(x+2y)2﹣(x+y)(3x﹣y)﹣5y2]÷(﹣x),其中x=﹣2,y= .20. 如图,已知∠A=50°,AB∥CD,CE平分∠ACD交AB于点E.求∠1的度数.
 21. 一个不透明的口袋里有5个除颜色外都相同的球,其中有2个红球,3个黄球.(1)、若从中随意摸出一个球,求摸出红球的可能性;(2)、若要使从中随意摸出一个球是红球的可能性为 ,求袋子中需再加入几个红球?22. 如图,两个正方形边长分别为a,b.
21. 一个不透明的口袋里有5个除颜色外都相同的球,其中有2个红球,3个黄球.(1)、若从中随意摸出一个球,求摸出红球的可能性;(2)、若要使从中随意摸出一个球是红球的可能性为 ,求袋子中需再加入几个红球?22. 如图,两个正方形边长分别为a,b. (1)、用a,b表示阴影部分的面积;(2)、如果a+b=7,ab=5,求阴影部分的面积.23. 如图,在四边形ABCD中, ,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.求证:
(1)、用a,b表示阴影部分的面积;(2)、如果a+b=7,ab=5,求阴影部分的面积.23. 如图,在四边形ABCD中, ,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.求证: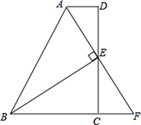 (1)、FC=AD;(2)、AB=BC+AD.24. 某中学的小明同学和朱老师一起从相同地点向同一方向跑步锻炼身体,朱老师先跑.当小明出发时,朱老师已经距起点200米了.他们距起点的距离s(米)与小明出发的时间t(秒)之间的关系如图所示(不完整).据图中给出的信息,解答下列问题:
(1)、FC=AD;(2)、AB=BC+AD.24. 某中学的小明同学和朱老师一起从相同地点向同一方向跑步锻炼身体,朱老师先跑.当小明出发时,朱老师已经距起点200米了.他们距起点的距离s(米)与小明出发的时间t(秒)之间的关系如图所示(不完整).据图中给出的信息,解答下列问题: (1)、在上述变化过程中,自变量是 , 因变量是;(2)、分别求朱老师和小明跑步的速度;(3)、当小明追上朱老师时,求小明距起点的距离是多少米?25. 如图(1)AB=9cm,AC⊥AB,BD⊥AB,AC=BD=7cm,点P在线段AB上以2cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动,它们运动的时间为t(s).
(1)、在上述变化过程中,自变量是 , 因变量是;(2)、分别求朱老师和小明跑步的速度;(3)、当小明追上朱老师时,求小明距起点的距离是多少米?25. 如图(1)AB=9cm,AC⊥AB,BD⊥AB,AC=BD=7cm,点P在线段AB上以2cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动,它们运动的时间为t(s). (1)、若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,请说明理由;(2)、在(1)的前提条件下,判断此时线段PC和线段PQ的位置关系,并证明;(3)、如图(2),将图(1)中的“AC⊥AB,BD⊥AB”为改“∠CAB=∠DBA=50°”,其他条件不变.设点Q的运动速度为xcm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由.
(1)、若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,请说明理由;(2)、在(1)的前提条件下,判断此时线段PC和线段PQ的位置关系,并证明;(3)、如图(2),将图(1)中的“AC⊥AB,BD⊥AB”为改“∠CAB=∠DBA=50°”,其他条件不变.设点Q的运动速度为xcm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由.