四川省遂宁市射洪市2020-2021学年七年级下学期期末数学试卷
试卷更新日期:2022-06-22 类型:期末考试
一、单选题
-
1. 在数轴上表示不等式x-1<0的解集,正确的是()A、
 B、
B、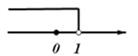 C、
C、 D、
D、 2. 下列等式变形正确的是( )A、由a=b,得4+a=4﹣b B、如果2x=3y,那么 C、由mx=my,得x=y D、如果3a=6b﹣1,那么a=2b﹣13. 若a>b,则( )A、a﹣1≥b B、b+1≥a C、a+1>b﹣1 D、a﹣1>b+14. 已知关于x的方程2x-a-5=0的解是x=-2,则a的值为( )A、1 B、 C、9 D、5. 已知|5x﹣2|=2﹣5x,则x的范围是( )A、 B、 C、 D、6. 长度分别为2,3,3,4的四根细木棒首尾相连,围成一个三角形(木棒允许连接,但不允许折断),得到的三角形的最长边长为( )A、4 B、5 C、6 D、77. 通过下面几个图形说明“锐角α,锐角β的和是锐角”,其中错误的例证图是( )A、
2. 下列等式变形正确的是( )A、由a=b,得4+a=4﹣b B、如果2x=3y,那么 C、由mx=my,得x=y D、如果3a=6b﹣1,那么a=2b﹣13. 若a>b,则( )A、a﹣1≥b B、b+1≥a C、a+1>b﹣1 D、a﹣1>b+14. 已知关于x的方程2x-a-5=0的解是x=-2,则a的值为( )A、1 B、 C、9 D、5. 已知|5x﹣2|=2﹣5x,则x的范围是( )A、 B、 C、 D、6. 长度分别为2,3,3,4的四根细木棒首尾相连,围成一个三角形(木棒允许连接,但不允许折断),得到的三角形的最长边长为( )A、4 B、5 C、6 D、77. 通过下面几个图形说明“锐角α,锐角β的和是锐角”,其中错误的例证图是( )A、 B、
B、 C、
C、 D、
D、 8. 将一副三角尺按如图所示的方式摆放,则∠α的大小为( )
8. 将一副三角尺按如图所示的方式摆放,则∠α的大小为( ) A、105° B、75° C、65° D、55°9. 下面的图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图形的是( )A、
A、105° B、75° C、65° D、55°9. 下面的图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图形的是( )A、 赵爽弦图
B、
赵爽弦图
B、 笛卡尔心形线
C、
笛卡尔心形线
C、 科克曲线
D、
科克曲线
D、 斐波那契螺旋线
10. 已知x,y互为相反数且满足二元一次方程组 , 则k的值是( )A、﹣1 B、0 C、1 D、211. 已知下列方程:①x﹣2=;②0.4x=1;③=2x﹣2;④x﹣y=6;⑤x=0.其中一元一次方程有( )A、2个 B、3个 C、4个 D、5个12. 程大位《直指算法统宗》:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚得几丁,意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,试问大、小和尚各多少人?设大和尚有x人,小和尚有y人,依题意列方程组正确的是( )A、 B、 C、 D、13. 如图所示,要使一个六边形木架在同一平面内不变形,至少还要再钉上( )根木条.
斐波那契螺旋线
10. 已知x,y互为相反数且满足二元一次方程组 , 则k的值是( )A、﹣1 B、0 C、1 D、211. 已知下列方程:①x﹣2=;②0.4x=1;③=2x﹣2;④x﹣y=6;⑤x=0.其中一元一次方程有( )A、2个 B、3个 C、4个 D、5个12. 程大位《直指算法统宗》:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚得几丁,意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,试问大、小和尚各多少人?设大和尚有x人,小和尚有y人,依题意列方程组正确的是( )A、 B、 C、 D、13. 如图所示,要使一个六边形木架在同一平面内不变形,至少还要再钉上( )根木条.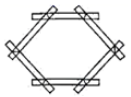 A、 B、 C、 D、14. 若关于x的不等式 只有2个正整数解,则a的取值范围为( )A、 B、 C、 D、15. 在某次演讲比赛中,五位评委给选手圆圆打分,得到互不相等的五个分数.若去掉一个最高分,平均分为x;去掉一个最低分,平均分为 ;同时去掉一个最高分和一个最低分,平均分为z,则A、 B、 C、 D、16. 若方程组 的解是 ,则方程组 的解是( )A、 B、 C、 D、17. 下列边长相等的正多边形能完成镶嵌的是( )A、2个正八边形和1个正三角形 B、3个正方形和2个正三角形 C、1个正五边形和1个正十边形 D、2个正六边形和2个正三角形18. 某班数学兴趣小组对不等式组讨论得到以下结论:
A、 B、 C、 D、14. 若关于x的不等式 只有2个正整数解,则a的取值范围为( )A、 B、 C、 D、15. 在某次演讲比赛中,五位评委给选手圆圆打分,得到互不相等的五个分数.若去掉一个最高分,平均分为x;去掉一个最低分,平均分为 ;同时去掉一个最高分和一个最低分,平均分为z,则A、 B、 C、 D、16. 若方程组 的解是 ,则方程组 的解是( )A、 B、 C、 D、17. 下列边长相等的正多边形能完成镶嵌的是( )A、2个正八边形和1个正三角形 B、3个正方形和2个正三角形 C、1个正五边形和1个正十边形 D、2个正六边形和2个正三角形18. 某班数学兴趣小组对不等式组讨论得到以下结论:①若a=5,则不等式组的解集为2<x≤5;②若a=1,则不等式组无解;③若不等式组无解,则a的取值范围为a≤2;④若不等式组有且只有两个整数解,则a的值可以为5.1,以上四个结论,正确的序号是( )
A、①②③ B、①③④ C、①②④ D、①②③④19. 如图,小明在操场试验:从点A出发沿直线前进20米来到达点B,向左转45°后又沿直线前进20米到达点C,再向左转45°后沿直线前进20米到达点D,…照这样走下去,小明第一次回到出发点A时所走的路程为( ) A、200米 B、160米 C、140米 D、120米20. 如图,△ABC中,∠ABC=∠ACB,∠A=50°,P是△ABC内的一点,且∠PBC=∠PCA,则∠BPC等于( )
A、200米 B、160米 C、140米 D、120米20. 如图,△ABC中,∠ABC=∠ACB,∠A=50°,P是△ABC内的一点,且∠PBC=∠PCA,则∠BPC等于( ) A、115° B、100° C、130° D、140°
A、115° B、100° C、130° D、140°二、填空题
-
21. 已知方程2x+3y-4=0,用含x的代数式表示y为 .22. 不等式 的非负整数解是 .23. 如果 ,那么xy= .24. x=2时,代数式2x2+(3﹣c)x+c的值是10,则当x=﹣3时,这个代数式的值为.25. 如图,△ABC绕顶点A逆时针旋转30°至△ADE,∠B=40°,∠DAC=50°,则∠E=.
 26. 如图,五边形ABCD中,∠1、∠2、∠3是它的三个外角,已知∠C=120°,∠E=90°,那么∠1+∠2+∠3=.
26. 如图,五边形ABCD中,∠1、∠2、∠3是它的三个外角,已知∠C=120°,∠E=90°,那么∠1+∠2+∠3=. 27. 如图,在△ABC中,D,E分别是边AB,AC上一点,将△ABC沿DE折叠,使点A的对称点A'落在边BC上,若∠A=50°,则∠1+∠2+∠3+∠4=.
27. 如图,在△ABC中,D,E分别是边AB,AC上一点,将△ABC沿DE折叠,使点A的对称点A'落在边BC上,若∠A=50°,则∠1+∠2+∠3+∠4=. 28. 如图,正六边形A1A2A3A4A5A6内部有一个正五边形B1B2B3B4B5 , 且A3A4 B3B4 , 直线l经过B2、B3 , 则直线l与A1A2的夹角α= .
28. 如图,正六边形A1A2A3A4A5A6内部有一个正五边形B1B2B3B4B5 , 且A3A4 B3B4 , 直线l经过B2、B3 , 则直线l与A1A2的夹角α= . 29. 如图,将ABC沿BC方向平移一定距离得到DEF,若AB=5,BE=3,DG=2,则图中阴影部分面积为 .
29. 如图,将ABC沿BC方向平移一定距离得到DEF,若AB=5,BE=3,DG=2,则图中阴影部分面积为 . 30. 若[x]表示不超过x的最大整数.如[π]=3,[4]=4,[﹣2.4]=﹣3.则下列结论:
30. 若[x]表示不超过x的最大整数.如[π]=3,[4]=4,[﹣2.4]=﹣3.则下列结论:①[﹣x]=﹣[x];
②若[x]=n,则x的取值范围是n≤x<n+1;
③x=﹣2.75是方程4x﹣[x]+5=0的一个解;
④当﹣1<x<1时,[1+x]+[1﹣x]的值为1或2.
其中正确的结论有 (写出所有正确结论的序号).
三、解答题
-
31.(1)、;(2)、.32.(1)、;(2)、.33. 如图1,AD、BC交于点O,得到的数学基本图形我们称之为‘8’字形ABCD.
 (1)、试说明:∠A+∠B=∠C+∠D;(2)、如图2,∠ABC和∠ADC的平分线相交于E,尝试用(1)中的数学基本图形和结论,猜想∠E与∠A、∠C之间的数量关系并说明理由.34. 如果一元一次方程的根是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程.(1)、在方程①3x﹣1=0,② x+1=0,③x﹣(3x+1)=﹣5中,不等式组 的关联方程是;(填序号)(2)、若不等式组 的一个关联方程的根是整数,则这个关联方程可以是;(写出一个即可)(3)、若方程3﹣x=2x,3+x=2(x+ )都是关于x的不等式组 的关联方程,直接写出m的取值范围.35. 为加快复工复产,某企业需运输批物资.据调查得知,2辆大货车与3辆小货车一次可以运输600箱;5辆大货车与6辆小货车一次可以运输1350箱.(1)、求1辆大货车和1辆小货车一次可以分别运输多少箱物资;(2)、计划用两种货车共12辆运输这批物资,每辆大货车一次需费用5 000元,每辆小货车一次需费用3000元.若运输物资不少于1500箱,且总费用小于54000元,请你列出所有运输方案,并指出哪种方案所需费用最少,最少费用是多少?36. 已知关于x,y的方程组 的解都为正数.(1)、求a的取值范围;(2)、已知 ,且 , ,求z的取值范围.37. ∠MON=90°,点A,B分别在OM、ON上运动(不与点O重合).(1)、如图①,AE、BE分别是∠BAO和∠ABO的平分线,随着点A、点B的运动,∠AEB=°
(1)、试说明:∠A+∠B=∠C+∠D;(2)、如图2,∠ABC和∠ADC的平分线相交于E,尝试用(1)中的数学基本图形和结论,猜想∠E与∠A、∠C之间的数量关系并说明理由.34. 如果一元一次方程的根是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程.(1)、在方程①3x﹣1=0,② x+1=0,③x﹣(3x+1)=﹣5中,不等式组 的关联方程是;(填序号)(2)、若不等式组 的一个关联方程的根是整数,则这个关联方程可以是;(写出一个即可)(3)、若方程3﹣x=2x,3+x=2(x+ )都是关于x的不等式组 的关联方程,直接写出m的取值范围.35. 为加快复工复产,某企业需运输批物资.据调查得知,2辆大货车与3辆小货车一次可以运输600箱;5辆大货车与6辆小货车一次可以运输1350箱.(1)、求1辆大货车和1辆小货车一次可以分别运输多少箱物资;(2)、计划用两种货车共12辆运输这批物资,每辆大货车一次需费用5 000元,每辆小货车一次需费用3000元.若运输物资不少于1500箱,且总费用小于54000元,请你列出所有运输方案,并指出哪种方案所需费用最少,最少费用是多少?36. 已知关于x,y的方程组 的解都为正数.(1)、求a的取值范围;(2)、已知 ,且 , ,求z的取值范围.37. ∠MON=90°,点A,B分别在OM、ON上运动(不与点O重合).(1)、如图①,AE、BE分别是∠BAO和∠ABO的平分线,随着点A、点B的运动,∠AEB=° (2)、如图②,若BC是∠ABN的平分线,BC的反向延长线与∠OAB的平分线交于点D
(2)、如图②,若BC是∠ABN的平分线,BC的反向延长线与∠OAB的平分线交于点D
①若∠BAO=60°,则∠D= ▲ .
②随着点A,B的运动,∠D的大小会变吗?如果不会,求∠D的度数;如果会,请说明理由.
(3)、如图③,延长MO至Q,延长BA至G,已知∠BAO,∠OAG的平分线与∠BOQ的平分线及其延长线相交于点E、F,在△中,如果有一个角是另一个角的3倍,求∠ABO的度数.