四川省达州市宣汉县2020-2021学年七年级下学期期末数学试卷
试卷更新日期:2022-06-22 类型:期末考试
一、单选题
-
1. 的计算结果是( )A、 B、 C、 D、2. 已知的三边长分别为 , , , 则 , , 的值可能分别是( )A、 , , B、 , , C、 , , D、 , ,3. 下面四个图形分别是节能、节水、低碳和绿色食品标志,在这四个标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 如图,直线l//m,等腰Rt△ABC,直角顶点C在直线l上,另一个顶点B在直线m上,若∠1=28°,则∠2=( )
4. 如图,直线l//m,等腰Rt△ABC,直角顶点C在直线l上,另一个顶点B在直线m上,若∠1=28°,则∠2=( ) A、17° B、62° C、73° D、75°5. 下列算式中,结果不等于的是( )A、 B、 C、 D、6. 如图,已知AD=AE,添加下列条件仍无法证明△ABE≌△ACD的是( )
A、17° B、62° C、73° D、75°5. 下列算式中,结果不等于的是( )A、 B、 C、 D、6. 如图,已知AD=AE,添加下列条件仍无法证明△ABE≌△ACD的是( )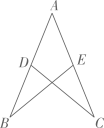 A、AB=AC B、∠B=∠C C、BE=CD D、∠ADC=∠AEB7. 在如图所示的正方形纸片上做随机扎针实验,则针头扎在阴影区域内的概率为( )
A、AB=AC B、∠B=∠C C、BE=CD D、∠ADC=∠AEB7. 在如图所示的正方形纸片上做随机扎针实验,则针头扎在阴影区域内的概率为( ) A、 B、 C、 D、8. 已知 ,则 ( )A、 B、 C、 D、529. 为了增强抗旱能力,保证今年夏粮丰收,某村新修建了一个蓄水池,这个蓄水池安装了两个进水管和一个出水管(两个进水管的进水速度相同)一个进水管和一个出水管的进出水速度如图(1)所示,某天0点到6点(至少打开一个水管),该蓄水池的蓄水量如图(2)所示,并给出以下三个论断;①0点到1点不进水,只出水;②1点到4点不进水,不出水;③4点到6点只进水,不出水.则一定正确的论断是( )
A、 B、 C、 D、8. 已知 ,则 ( )A、 B、 C、 D、529. 为了增强抗旱能力,保证今年夏粮丰收,某村新修建了一个蓄水池,这个蓄水池安装了两个进水管和一个出水管(两个进水管的进水速度相同)一个进水管和一个出水管的进出水速度如图(1)所示,某天0点到6点(至少打开一个水管),该蓄水池的蓄水量如图(2)所示,并给出以下三个论断;①0点到1点不进水,只出水;②1点到4点不进水,不出水;③4点到6点只进水,不出水.则一定正确的论断是( ) A、①③ B、②③ C、③ D、①②10. 某同学在计算时,把3写成后,发现可以连续运用两数和乘以这两数差公式计算:.请借鉴该同学的经验,计算:( )A、 B、 C、1 D、2
A、①③ B、②③ C、③ D、①②10. 某同学在计算时,把3写成后,发现可以连续运用两数和乘以这两数差公式计算:.请借鉴该同学的经验,计算:( )A、 B、 C、1 D、2二、填空题
-
11. 纳米是一种长度单位,纳米米,冠状病毒的直径为纳米,用科学记数法表示为米.12. 如图,直线AB,CD相交于点O,OE⊥CD. 若∠1= 40°,则∠BOE的大小是.
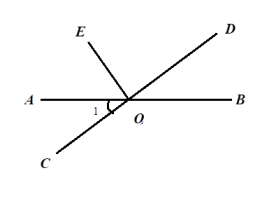 13. 下列各式:①;②;③;④.其中计算正确的有(填序号即可).14. 如图,在中,平分 , 平分 , 若 , 则.
13. 下列各式:①;②;③;④.其中计算正确的有(填序号即可).14. 如图,在中,平分 , 平分 , 若 , 则. 15. 如图(1),已知 ,D为 的角平分线上一点,连接BD,CD;如图(2),已知 ,D,E为 的角平分线上两点,连接BD,CD,BE,CE;如图(3),已知 ,D,E , F为 的角平分线上三点,连接BD,CD,BE,CE,BF,CF;……,依此规律,第7个图形中有全等三角形的对数是 .
15. 如图(1),已知 ,D为 的角平分线上一点,连接BD,CD;如图(2),已知 ,D,E为 的角平分线上两点,连接BD,CD,BE,CE;如图(3),已知 ,D,E , F为 的角平分线上三点,连接BD,CD,BE,CE,BF,CF;……,依此规律,第7个图形中有全等三角形的对数是 .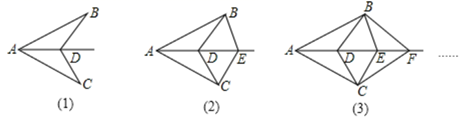 16. 如图,在中, , 射线 , 点E从点A出发沿射线以的速度运动,当点E先出发后,点F也从点B出发,沿射线以的速度运动,分别连接.设点E运动的时间为 , 其中 , 当时,.
16. 如图,在中, , 射线 , 点E从点A出发沿射线以的速度运动,当点E先出发后,点F也从点B出发,沿射线以的速度运动,分别连接.设点E运动的时间为 , 其中 , 当时,.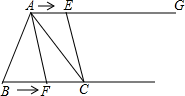
三、解答题
-
17. 如图,.求证:∥.在下面的括号中填上推理依据.

证明:∵(已知)
∴∥( )
∴∠5+∠CAB=180°( )
∵ (已知)
∴∠6+∠CAB=180°(等式的性质)
∴∥( )
∴( )
∵ (已知)
∴ (等量代换)
∴∥( )
18.(1)、计算(2)、先化简,再求值: , 其中 ,19. 如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AB∥DE,∠A=∠D. (1)、求证:△ABC≌△DEF;(2)、若BE=10m,BF=3m,则FC的长度为 m.20. 如图所示,在正方形网格上有一个 , 、、在格点上.
(1)、求证:△ABC≌△DEF;(2)、若BE=10m,BF=3m,则FC的长度为 m.20. 如图所示,在正方形网格上有一个 , 、、在格点上. (1)、画关于直线的对称图形(不写画法,保留作图痕迹);(2)、若网格上的每个小正方形的边长都为 , 求的面积.21. 为了解中考体育科目训练情况,某县从全县九年级学生中随机抽取了部分学生进行了一次中考体育科目测试(把测试结果分为四个等级:级:优秀;级:良好;级:及格;级:不及格),并将测试结果绘成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题:
(1)、画关于直线的对称图形(不写画法,保留作图痕迹);(2)、若网格上的每个小正方形的边长都为 , 求的面积.21. 为了解中考体育科目训练情况,某县从全县九年级学生中随机抽取了部分学生进行了一次中考体育科目测试(把测试结果分为四个等级:级:优秀;级:良好;级:及格;级:不及格),并将测试结果绘成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题: (1)、本次抽样测试的学生人数是人数是;(2)、扇形统计图中的度数是 ▲ , 并把条形统计图补充完整;(3)、该县九年级有学生名,如果全部参加这次中考体育科目测试,请估计不及格的人数;(4)、测试老师想从位同学(分别记为、、 , 其中为小明)中随机选择两位同学了解平时训练情况,请列举出所有结果,并求出选中小明的概率.22. 小明某天上午时骑自行车离开家,时回到家,他有意描绘了离家的距离与时间的变化情况(如图所示).
(1)、本次抽样测试的学生人数是人数是;(2)、扇形统计图中的度数是 ▲ , 并把条形统计图补充完整;(3)、该县九年级有学生名,如果全部参加这次中考体育科目测试,请估计不及格的人数;(4)、测试老师想从位同学(分别记为、、 , 其中为小明)中随机选择两位同学了解平时训练情况,请列举出所有结果,并求出选中小明的概率.22. 小明某天上午时骑自行车离开家,时回到家,他有意描绘了离家的距离与时间的变化情况(如图所示). (1)、图象表示了哪两个变量之间的关系?哪个是自变量?哪个是因变量?(2)、时和时,他分别离家多远?(3)、他到达离家最远的地方是什么时间?离家多远?(4)、时到时他行驶了多少千米?(5)、他可能在哪段时间内休息,并吃午餐?(6)、他由离家最远的地方返回时的平均速度是多少?23. 如图,在等腰三角形ABC中,AB=AC,AD是BC边上的高,点E,F分别是边AB,AC的中点,且EF∥BC.
(1)、图象表示了哪两个变量之间的关系?哪个是自变量?哪个是因变量?(2)、时和时,他分别离家多远?(3)、他到达离家最远的地方是什么时间?离家多远?(4)、时到时他行驶了多少千米?(5)、他可能在哪段时间内休息,并吃午餐?(6)、他由离家最远的地方返回时的平均速度是多少?23. 如图,在等腰三角形ABC中,AB=AC,AD是BC边上的高,点E,F分别是边AB,AC的中点,且EF∥BC.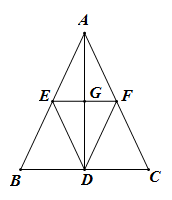 (1)、试说明△AEF是等腰三角形;(2)、试比较DE与DF的大小关系,并说明理由.24. 把一个长为 , 宽为的长方形沿图1中虚线用剪刀均分成四个小长方形,然后拼成—个正方形(如图2).
(1)、试说明△AEF是等腰三角形;(2)、试比较DE与DF的大小关系,并说明理由.24. 把一个长为 , 宽为的长方形沿图1中虚线用剪刀均分成四个小长方形,然后拼成—个正方形(如图2). (1)、请用两种方法求出图2中阴影部分的面积;(直接用含的式子表示)
(1)、请用两种方法求出图2中阴影部分的面积;(直接用含的式子表示)方法1:;
方法2:;
(2)、根据(1)中的结论,请你写出下列三个式子间的等量关系:;(3)、根据(2)中的等量关系.解决如下问题:已知实数满足 , 请求出的值.25. 如图,在 中,高线 , 相交于点 , , , . (1)、证明: .(2)、线段 .(3)、 是直线 上的一点,且 ,动点 从点 出发,沿线段 以每秒1个单位长度的速度向终点 运动,动点 从点 出发,沿射线 以每秒4个单位长度的速度运动, , 两点同时出发,当点 到达 点时, , 两点同时停止运动,设点 的运动时间为 秒,则是否存在 值,使得以点 , , 为顶点的三角形与以点 , , 为顶点的三角形全等?若存在,请求出符合条件的 值;若不存在,请说明理由.
(1)、证明: .(2)、线段 .(3)、 是直线 上的一点,且 ,动点 从点 出发,沿线段 以每秒1个单位长度的速度向终点 运动,动点 从点 出发,沿射线 以每秒4个单位长度的速度运动, , 两点同时出发,当点 到达 点时, , 两点同时停止运动,设点 的运动时间为 秒,则是否存在 值,使得以点 , , 为顶点的三角形与以点 , , 为顶点的三角形全等?若存在,请求出符合条件的 值;若不存在,请说明理由.