四川省达州市渠县2020-2021学年七年级下学期期末数学试卷

试卷更新日期：2022-06-22 类型：期末考试

进入出卷网下载

一、单选题

1. $202 1^{- 1}$ 的倒数是（）

A、 $\frac{1}{2021}$ B、 $- \frac{1}{2021}$ C、2021 D、－2021

查看试题解析
2. 下列各式中，计算结果为a⁶的是（　　）

A、a²•a³ B、a³+a³ C、a¹²÷a² D、（a²）³

查看试题解析
3. 如图， $A B / / C D$ ， $A E$ 交 $D F$ 与 $C$ ， $∠ E C F = 134 °$ ，则 $∠ A$ 的度数是（）

A、 $54 °$ B、 $46 °$ C、 $45 °$ D、 $44 °$

查看试题解析
4. 若一个三角形的三边长分别为3，7，x，则x的值可能是（）

A、6 B、3 C、2 D、11

查看试题解析
5. 观察下列尺规作图的痕迹：

其中，能够说明 $A B > A C$ 的是（）

A、①② B、②③ C、①③ D、③④

查看试题解析
6. 如图，火车匀速通过隧道（隧道长大于火车长）时，火车在隧道内的长度y与火车进入隧道的时间x之间的关系用图象描述大致是（）

A、 B、 C、 D、

查看试题解析
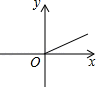7. 若代数式x²﹣16x+k²是完全平方式，则k等于（）

A、6 B、64 C、±64 D、±8

查看试题解析
8. 如图，在方格纸中，以AB为一边作△ABP ，使之与△ABC全等，从P₁ ， P₂ ， P₃ ， P₄四个点中找出符合条件的点P的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{2}$ C、 $\frac{3}{4}$ D、1

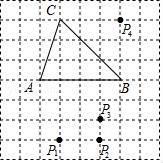查看试题解析
9. 如图，在等边△ABC中，点E是AC边的中点，点P是△ABC的中线AD上的动点，且AD＝6，则EP+CP的最小值是（）

A、12 B、9 C、6 D、3

查看试题解析
10. 如图，已知∠MON＝30°，点A₁ ， A₂ ， A₃ ， …在射线ON上，点B₁ ， B₂ ， B₃ ， …在射线OM上，△A₁B₁A₂ ， △A₂B₂A₃ ， △A₃B₃A₄ ， …均为等边三角形，若OA₁＝2，则△A₆B₆A₇的边长为（）

A、16 B、32 C、64 D、128

查看试题解析

二、填空题

11. 计算： $3^{2020} \times 3^{- 2021} =$ .

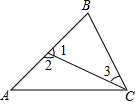
查看试题解析
12. 蜜蜂建造的蜂巢既坚固又省料，其厚度约为0.000073米，将0.000073用科学记数法表示为．

查看试题解析
13. 袋中装有3个黑球，6个白球（这些球除颜色外都相同），随机摸出一个球，恰好是白球的概率是 .

查看试题解析
14. 如图，下列结论：①∠2与∠3是内错角；②∠1与∠A是同位角；③∠A与∠B是同旁内角；④∠B与∠ACB不是同旁内角，其中正确的是 .（只填序号）

查看试题解析
15. 如图，在△ACD中，∠CAD＝90°，AC＝6，AD＝8，AB∥CD，E是CD上一点，BE交AD于点F，当AB+CE＝CD时，则图中阴影部分的面积为 .

查看试题解析
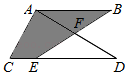16. 如图①．在正方形 $A B C D$ 的边 $B C$ 上有一点E ，连接 $A E$ ．点P从正方形的顶点A出发，沿 $A \to D \to C$ 以 $1cm/s$ 的速度匀速运动到点C．图②是点P运动时， $△ A P E$ 的面积 $y ({cm}^{2})$ 随时间 $x (s)$ 变化的函数图象．当 $x = 7$ 时，y的值为．

查看试题解析

三、解答题

17. 计算.

(1)、4×（2n）²÷（2n^﹣¹）².

(2)、（﹣1）²⁰²⁰×（π﹣2）⁰﹣|﹣5|﹣（﹣ $\frac{1}{2}$ ）^﹣³.

查看试题解析
18. 已知x＝ $\frac{1}{27}$ ， y＝﹣27，求代数式x（x+2y）﹣（x﹣1）²﹣2x的值.

查看试题解析
19. 已知：两直线AB $∥$ CD，E是平面内任一点（不在AB、CD上）.

(1)、如图1所示，E在射线AB与CD之间时，请说明∠AEC=∠A+∠C的理由.

(2)、如图2所示，点E在AB与CD的上方时，请探索∠A，∠C，∠AEC三者的数量关系，并说明理由.

查看试题解析
20. 甲、乙在一条直线跑道上匀速跑步，乙先跑.甲出发时，乙已经距起点100米了，他们距起点的距离s（米）与甲出发的时间t（秒）之间的关系如图（不完整）.根据图中信息，解答下列问题.

(1)、在上述变化过程中，自变量是，因变量是.

(2)、甲的速度为米/秒，乙的速度为米/秒.

(3)、当甲追上乙时，求甲距起点的距离.

查看试题解析
21. 如图1，在边长为1的9×9正方形网格中，老师请同学们过点C画线段AB的垂线．如图2，小明在多媒体展台上展示了他画出的图形．请你利用所学知识判断并说明直线CD是否为线段AB的垂线．（点A，B，C，D，E，F都是小正方形的顶点）

查看试题解析
22. 境外许多国家的疫情尚在继续蔓延，疫情防控不可松懈.如图是某国截止5月31日新冠病毒感染人数的扇形统计图和折线统计图.根据图表信息，回答下列问题.

(1)、截止5月31日该国新冠肺炎感染总人数累计为万人，扇形统计图中40﹣59岁感染人数对应圆心角的度数为°.

(2)、请直接在图中补充完整该国新冠肺炎感染人数的折线统计图.

(3)、在该国所有新冠肺炎感染病例中随机地抽取1人，求该患者年龄为60岁或60岁以上的概率.

查看试题解析
23. 如图1是一个长为4b、宽为a的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后用四块小长方形拼成一个“回形”正方形（如图2）.

(1)、观察图2请你写出（a+b）²、（a﹣b）²、ab之间的等量关系是.

(2)、根据（1）中的结论，若x+y＝5，xy＝ $\frac{9}{4}$ ，求x﹣y的值.

(3)、变式应用：若（2019﹣m）²+（m﹣2021）²＝20，求（2019﹣m）（m﹣2021）的值.

查看试题解析
24. 如图，在等边三角形ABC的外侧作直线AP，点C关于直线AP的对称点为点D，连接AD，BD，其中BD交直线AP于点E.

(1)、依题意补全图形.

(2)、若∠PAC＝20°，求∠AEB的度数；

(3)、连接CE，求证：BE＝AE+CE.

查看试题解析
25. 【问题】在四边形ABCD中，AB＝AD，∠BAD＝120°，∠B＝∠ADC＝90°，E、F分别是BC、CD上的点，且∠EAF＝60°，试探究图1中线段BE、EF、FD之间的数量关系.

(1)、【探索】有同学认为：延长FD到点G，使DG＝BE，连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，则可得到BE、EF、FD之间的数量关系是 .

(2)、【延伸】在四边形ABCD中如图2，AB＝AD，∠B+∠D＝180°，E、F分别是BC、CD上的点，∠EAF＝ $\frac{1}{2}$ ∠BAD，上述结论是否仍然成立？说明理由.

(3)、【构造运用】如图3，在某次搜救行动中，甲艇在指挥中心（O处）北偏西30°的A处，乙艇在O点的南偏东70°的B处，且AO＝BO，接到行动指令后，甲艇向正东方向以60海里/小时的速度前进，乙艇沿北偏东50°的方向以80海里/小时的速度前进1.5小时后，甲、乙两艇分别到达E，F处，∠EOF＝70°，试求此时甲、乙两艇之间的距离.

查看试题解析