四川省成都市温江区2020-2021学年七年级下册期末数学试卷

试卷更新日期：2022-06-22 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 有一种花粉的直径是0.000064米，将0.000064用科学记数法表示应为（）

A、 $6.4 \times 1 0^{- 4}$ B、 $0.64 \times 1 0^{- 4}$ C、 $64 \times 1 0^{- 5}$ D、 $6.4 \times 1 0^{- 5}$

查看试题解析
3. 下列长度的三条线段，能组成三角形的是（）

A、4，5，6 B、3，5，9 C、3，4，7 D、5，6，11

查看试题解析
4. 下列事件中，是必然事件的是（）

A、掷一枚质地均匀的硬币，一定正面向上 B、车辆随机到达一个路口，遇到红灯 C、任意买一张电影票，座位号是2的倍数 D、将油滴在水中，油会浮在水面上

查看试题解析
5. 下列计算错误的是（）

A、 ${(x^{2})}^{3} = x^{6}$ B、 $- x^{2} \cdot (- x)^{2} = - x^{4}$ C、 $x^{3} + x^{2} = x^{5}$ D、 ${(- x^{2} y)}^{3} = - x^{6} y^{3}$

查看试题解析
6. 柿子熟了，从树上落下来.下面可以大致刻画出柿子下落过程（即落地前）的速度变化情况的是（）

A、 B、 C、 D、

查看试题解析
7. 下列说法错误的是（）

A、同旁内角相等，两直线平行 B、内错角相等，两条直线平行 C、对顶角相等 D、平行于同一条直线的两条直线平行

查看试题解析
8. 如图，小明站在堤岸的A点处，正对他的S点停有一艘游艇.他想知道这艘游艇距离他有多远，于是他沿堤岸走到电线杆B旁，接着再往前走相同的距离到达C点.然后他向左直行，当看到电线杆与游艇在一条直线上时停下来，此时他位于D点.那么C，D两点间的距离就是在A点处小明与游艇的距离.在这个问题中，可作为证明 $△ S A B ≌ △ D C B$ 的依据的是（）

A、 $S A S$ 或 $S S S$ B、 $A A S$ 或 $S S S$ C、 $A S A$ 或 $A A S$ D、 $A S A$ 或 $S A S$

查看试题解析
9. 如图，在已知的 $△ A B C$ 中，按以下步骤作图：①分别以A，B为圆心，以大于 $\frac{1}{2} A B$ 的长为半径作弧，两弧相交于两点E，F；②作直线 $E F$ 交 $B C$ 于点D，连接 $A D$ .若 $∠ C = 60 °$ ， $∠ C A D = 2 ∠ A D C$ ，则 $∠ B A C$ 的度数为（）

A、 $90 °$ B、 $100 °$ C、 $110 °$ D、 $120 °$

查看试题解析
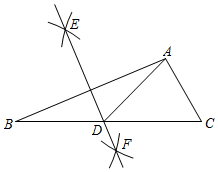10. 把七巧板按如图所示，进行①～⑦编号，①～⑦号分别对应着七巧板的七块，如果编号③对应的面积等于1，则由这七块拼成的正方形的面积等于（）

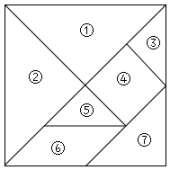A、12 B、16 C、18 D、20

查看试题解析

二、填空题

11. n为正整数，若 $a^{7} \div a^{n} = a^{4}$ ，则 $n =$ .

查看试题解析
12. 如图，在长方形 $A B C D$ 中有一个半径为1的半圆， $A B = 1$ 、 $B C = 2$ ，在长方形 $A B C D$ 中随机投一粒小米，则小米落在半圆内的概率是.

查看试题解析
13. 如图， $△ A B C$ 是等边三角形， $B D = C E$ ，则 $∠ A F B$ 的度数为.

查看试题解析
14. 若 $a^{2} + b^{2} = 7 ， a - b = 3$ ，则 $a b$ 的值为.

查看试题解析
15. 如图，在 $△ A B C$ 中， $A D$ 为 $△ A B C$ 的中线，点E、F为 $A C$ 的三等分点，若 $△ A B C$ 的面积等于18，则 $△ D E F$ 的面积为.

查看试题解析

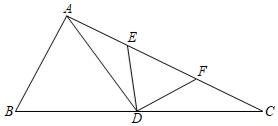
三、解答题

16.

(1)、计算： $(- 1)^{2021} + {(- \frac{1}{2})}^{- 2} - (π - 3.14)^{0} - | - 3 |$

(2)、先化简，再求值： $[(2 x + y) (2 x - y) + (2 x - y)^{2}] \div 2 x$ ，其中 $x = 1$ ， $y = 2$ .

查看试题解析
17.

(1)、如图，已知 $A C$ 、 $B C$ 分别是 $∠ B A D$ 、 $∠ A B E$ 的平分线，且 $∠ 1 + ∠ 2 = ∠ A C B$ .求证： $A D / / B E$ .

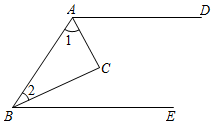(2)、一个质地均匀的骰子每个面上分别刻有1、2、3、4、5、6点，任意掷出骰子后
①求掷出的点数不大于4的概率；
②求掷出的点数能被3整除的概率.

查看试题解析

18.

(1)、如图，

A E / / B C

，

A B = B C

，

C D ⊥ A B

于点D，若

∠ A C D = 24 °

，求

∠ C A E

的度数.

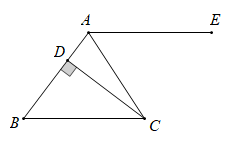(2)、距离地面越高温度越低，下表给出了距离地面高度与所在位置的温度之间的大致关系.根据下表，请回答以下问题.

距离地面高度（千米）	0	1	2	3	4
所在位置的温度（ $℃$ ）	30	24	18	12	6

①如果用x表示距离地面的高度用y表示温度，则y与x之间的关系式是什么？

②民航飞机通常在海拔7000至12000的高度飞行，某飞机在距离地面10000米的高空飞行计算此时飞机所在高空的温度（假设当时所在位置的地面温度为 $30 ℃$ ）.

查看试题解析

19.

(1)、a，b，c是三个连续的正偶数，以b为边长作正方形，分别以a，c为长和宽作长方形.
①正方形和长方形的周长是否相等？请说明理由；
②哪个图形的面积大？大多少？

(2)、已知 $△ A B C$ 中， $B D ⊥ A C$ ， $C E ⊥ A B$ ， $B D$ 、 $C E$ 交于点F， $E A = E F$ .求证： $A C = B F$ .

查看试题解析
20. 如图，在长方形 $A B C D$ 中， $A B = 4 c m$ ， $B C = 6 c m$ ，点P从点B出发，以 $1 c m$ /秒的速度沿 $B C$ 向点C运动，点P到达C点时，运动停止.

(1)、如图1，设点P的运动时间为t秒，则 $S_{△ D C P} =$ .（用t代数式表示）

(2)、如图2，当点P从点B开始运动的同时，点Q从点C出发，以 $v c m$ /秒的速度沿 $C D$ 向点D运动，是否存在这样v的值，使得在某一时刻阴影部分的两个直角三角形全等？若存在，请求出v的值；若不存在，请说明理由.

查看试题解析
21. 如图， $C A = C B$ ， $C A ⊥ C B$ ， $∠ E C F = 45 °$ ， $C D = C F$ ， $∠ A C D = ∠ B C F$ .

(1)、求 $∠ A C E + ∠ B C F$ 的度数；

(2)、以E为圆心，以 $A E$ 长为半径作弧；以F为圆心，以 $B F$ 长为半径作弧，两弧交于点G，试探索 $△ E F G$ 的形状？是锐角三形，直角三角形还是钝角三角形？请说明理由.

查看试题解析