四川省成都市青羊区2020-2021学年七年级下学期期末数学试卷

试卷更新日期：2022-06-22 类型：期末考试

进入出卷网下载

一、单选题

1. 已知某种感冒病毒的直径为0.000000823米，将0.000000823用科学记数法表示为（）

A、8.23×10^﹣⁶ B、8.23×10^﹣⁷ C、8.23×10⁶ D、8.23×10^﹣⁸

查看试题解析
2. 2021年3月20日三星堆遗址的最新考古发现又一次让世界为之瞩目，下列三星堆文物图案中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 若代数式x²+kx+9是完全平方式，则k的值为（）

A、6 B、-6 C、±6 D、±9

查看试题解析
4. 下列计算正确的是（）

A、8ab﹣3a＝5b B、（﹣3a²b）²＝6a⁴b² C、（a+1）²＝a²+1 D、2a²b÷b＝2a²

查看试题解析
5. 如图，现要从村庄 $A$ 修建一条连接公路 $C D$ 的最短小路，过点 $A$ 作 $A B ⊥ C D$ 于点 $B$ ，沿 $A B$ 修建公路，则这样做的理由是（）

A、垂线段最短 B、两点之间，线段最短 C、过一点可以作无数条直线 D、两点确定一条直线

查看试题解析
6. 如图，直线l₁∥l₂且与直线l₃相交于A、C两点.过点A作AD⊥AC交直线l₂于点D.若∠BAD＝35°，则∠ACD＝（）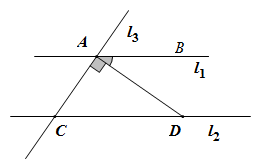

A、35° B、45° C、55° D、70°

查看试题解析
7. 如果（x+1）（3x+a）的乘积中不含x的一次项，则a为（）

A、3 B、﹣3 C、 $\frac{1}{3}$ D、﹣ $\frac{1}{3}$

查看试题解析
8. 在测量一个小口圆形容器的壁厚时，小明用“X型转动钳”按如图方法进行测量，其中OA＝OD，OB＝OC，测得AB＝5厘米，EF＝6厘米，圆形容器的壁厚是（　　）

A、5厘米 B、6厘米 C、2厘米 D、 $\frac{1}{2}$ 厘米

查看试题解析
9. 如图，已知在△ABC中AB＝AC，AB＝8，BC＝5，分别以A、B两点为圆心，大于 $\frac{1}{2}$ AB的长为半径画圆弧，两弧分别相交于点E、F.直线EF与AC相交于点D，则△BDC的周长为（）

A、15 B、13 C、11 D、10

查看试题解析
10. 柿子熟了，从树上落下来.下面可以大致刻画出柿子下落过程（即落地前）的速度变化情况的是（）

A、 B、 C、 D、

查看试题解析

二、填空题

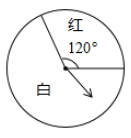
11. 计算：16x³÷（8x）＝.

查看试题解析
12. 已知x²﹣y²＝21，x﹣y＝3，则x+y＝.

查看试题解析
13. 转动如图所示的转盘，当转盘停止时，指针落在红色区域的概率是.

查看试题解析
14. 如图，在Rt△ABC中，∠CAB＝90°，∠ABC＝70°，AF平分∠CAB，交BC于点D.过点C作CE⊥AF于点E，则∠ECD的度数为.

查看试题解析
15. 若3^m＝6，3ⁿ＝2，则3^m+n的值为.

查看试题解析
16. 已知某快递公司的收费标准为：寄一件物品不超过5千克，收费14元；超过5千克的部分每千克加收3元，小明在该快递公司寄一件9千克的物品，需要付费元.

查看试题解析
17. 如图，D为△ABC中BC边上一点，AB＝CB，AC＝AD，∠BAD＝36°，则∠C的度数是.

查看试题解析
18. 如图AB $/ /$ DE，BF平分∠ABC，反向延长射线BF，与∠EDC的平分线DG相交于点P，若∠BPD＝44°，则∠C＝.

查看试题解析
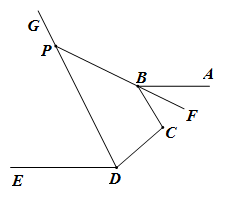19. 如图，在Rt△ABC中，∠ABC＝90°，AB＝BC，点D为三角形右侧外一点.且∠BDC＝45°.连接AD，若△ACD的面积为 $\frac{9}{8}$ ，则线段CD的长度为 .

查看试题解析

三、解答题

20. 计算：

(1)、2²×（2021）⁰+ $(- \frac{1}{2})^{- 3}$ +|﹣3|.

(2)、（2xy²）²•（﹣6x³y）÷（3x⁴y⁴）.

查看试题解析
21. 先化简，再求值：[（3x+y）²﹣9（x﹣y）（x+y）]÷（2y），其中x＝3，y＝﹣2.

查看试题解析
22. 如图，在四边形ABCD中，AB∥CD，连接BD，点E在BD上，连接CE，若∠1＝∠2，AB＝ED.

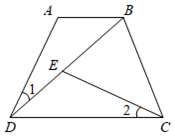(1)、求证：BD＝CD.

(2)、若∠A＝120°，∠BDC＝2∠1，求∠DBC的度数.

查看试题解析
23. 如图，在边长为单位1的正方形网格中有 $△$ ABC.

(1)、在图中画出 $△$ ABC关于直线MN成轴对称的图形 $△$ A₁B₁C₁；

(2)、求 $△$ ABC的面积：

(3)、在直线MN上有一点P使得PA+PB的值最小，请在图中标出点P的位置.

查看试题解析

24. 为庆祝中国共产党成立100周年，某校开展以学习“四史”（党史、新中国史、改革开放史、社会主义发展史）为主题的书画展，为了解作品主题分布情况，在学生上交的作品中，随机抽取了50份进行统计，并根据调查统计结果绘制了统计图表（频率＝

\frac{频 数}{总 数}

）：

主题	频数	频率
A党史	6	0.12
B新中国史	20	m
C改革开放史		0.18
D社会主义发展史	15	n
合计	50	1

请结合上述信息完成下列问题：

(1)、m＝， n＝．

(2)、请补全频数分布直方图．

(3)、若该校要同时开设两门课程（例如，课程BC和课程CB代表同一种情况），请直接写出同时开设课程BC的概率．

查看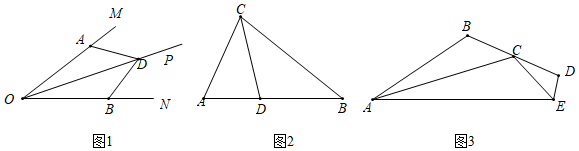试题解析

25.

(1)、如图1，射线OP平分∠MON，在射线OM，ON上分别截取线段OA，OB，使OA＝OB，在射线OP上任取一点D，连接AD，BD.求证：AD＝BD.

(2)、如图2，在Rt△ABC中，∠ACB＝90°，∠A＝60°，CD平分∠ACB，求证：BC＝AC+AD.

(3)、如图3，在四边形ABDE中，AB＝9，DE＝1，BD＝6，C为BD边中点，若AC平分∠BAE，EC平分∠AED，∠ACE＝120°，求AE的值.

查看试题解析
26. 解决下列问题：

(1)、已知x+3y＝7，xy＝2，求x﹣3y的值；

(2)、已知等腰△ABC的三边a、b、c为整数，且满足a²+b²＝4a+10b﹣29，求△ABC的周长.

查看试题解析
27. 甲、乙两个工程队分别同时铺设两条公路，所铺设公路的长度y（m）与铺设时间x（h）之间的关系如图所示，根据图象所提供的信息分析，解决下列问题：

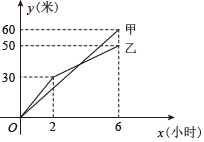(1)、在2时～6时段时，乙队的工作效率为m/h；

(2)、分别求出乙队在0时～2时段和2时～6时段，y与x的关系式，并求出甲乙两队所铺设公路长度相等时x的值；

(3)、求出当两队所铺设的公路长度之差为5m时x的值.

查看试题解析
28. 在△ABD中∠A＝45°，BC⊥AD于点C，E为AB上一点，连接DE交BC于点F，且∠ADE＝∠CBD.

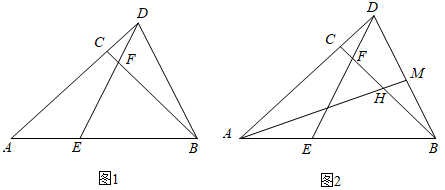(1)、如图1，求证：DE＝BD.

(2)、如图2，作AM⊥BD于点M，交BC于点H，判断AH与BD的数量关系，并证明.

(3)、在（2）的条件下，当CH：BH＝4：7，△ADE的面积为 $\frac{15}{2}$ 时，
①求线段AD的值；

②设AH＝a，用含a的代数式表示线段BM的值.

查看试题解析