四川省成都市金牛区2020-2021学年七年级下学期期末数学试卷
试卷更新日期:2022-06-22 类型:期末考试
一、单选题
-
1. 下列四个图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列计算正确的是( )A、 B、 C、 D、3. 据医学研究:新型冠状病毒的平均米,米用科学记数法表示为( )A、米 B、米 C、米 D、米4. 如图,已知 , , 则( )
2. 下列计算正确的是( )A、 B、 C、 D、3. 据医学研究:新型冠状病毒的平均米,米用科学记数法表示为( )A、米 B、米 C、米 D、米4. 如图,已知 , , 则( )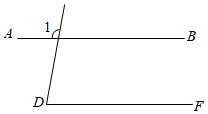 A、 B、 C、 D、5. 下列事件中,是必然事件的是( )A、买一张电影票,座位号是3的倍数 B、一个盒子装有 个红球和 个白球,除颜色外其它完全相同,同时摸出两个球,一定会摸到红球 C、掷一枚质地均匀的硬币,正面向上 D、走过一个红绿灯路口时,前方正好是红灯6. 若 , 则 , 的值分别为( )A、 , B、 , C、 , D、 ,7. 如图,有一池塘,要测池塘两端A,B的距离,可先在平地上取一个直接到达A和B的点C,连接AC并延长到D,使CD=CA,连接BC并延长到E,使CE=CB,连接DE,那么量出DE的长,就是A、B的距离.我们可以证明出△ABC≌△DEC,进而得出AB=DE,那么判定△ABC和△DEC全等的依据是( )
A、 B、 C、 D、5. 下列事件中,是必然事件的是( )A、买一张电影票,座位号是3的倍数 B、一个盒子装有 个红球和 个白球,除颜色外其它完全相同,同时摸出两个球,一定会摸到红球 C、掷一枚质地均匀的硬币,正面向上 D、走过一个红绿灯路口时,前方正好是红灯6. 若 , 则 , 的值分别为( )A、 , B、 , C、 , D、 ,7. 如图,有一池塘,要测池塘两端A,B的距离,可先在平地上取一个直接到达A和B的点C,连接AC并延长到D,使CD=CA,连接BC并延长到E,使CE=CB,连接DE,那么量出DE的长,就是A、B的距离.我们可以证明出△ABC≌△DEC,进而得出AB=DE,那么判定△ABC和△DEC全等的依据是( ) A、SSS B、SAS C、ASA D、AAS8. 将一张长方形纸沿向右上折叠,折叠后图形如图所示,为折痕,已知 , 则的度数为( )
A、SSS B、SAS C、ASA D、AAS8. 将一张长方形纸沿向右上折叠,折叠后图形如图所示,为折痕,已知 , 则的度数为( ) A、 B、 C、 D、9. 如图,点D在AB上.点E在AC上,AB=AC . 增加下列一个条件后,仍不能判定△ABE≌△ACD的是( )
A、 B、 C、 D、9. 如图,点D在AB上.点E在AC上,AB=AC . 增加下列一个条件后,仍不能判定△ABE≌△ACD的是( ) A、∠AEB=∠ADC B、∠B=∠C C、AE=AD D、BE=CD10. 小明从家骑单车上学,当他骑了一段时,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与离家的距离的关系示意图,根据图中的信息回答下列问题,则下列说法错误的是( )
A、∠AEB=∠ADC B、∠B=∠C C、AE=AD D、BE=CD10. 小明从家骑单车上学,当他骑了一段时,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与离家的距离的关系示意图,根据图中的信息回答下列问题,则下列说法错误的是( ) A、小明家到学校的路程是米 B、小明在书店停留了分钟 C、本次上学途中,小明一共行驶了米 D、若骑单车的速度大于米/分就有安全隐患.在整个上学的途中,小明骑车有分钟的超速骑行,存在安全隐患.
A、小明家到学校的路程是米 B、小明在书店停留了分钟 C、本次上学途中,小明一共行驶了米 D、若骑单车的速度大于米/分就有安全隐患.在整个上学的途中,小明骑车有分钟的超速骑行,存在安全隐患.二、填空题
-
11. 计算:(2a+b)(2a﹣b)= .12. 一个口袋中装有个白球、个红球,这些球除颜色外完全相同,充分搅匀后随机摸出一球是白球的概率为.13. 如图,在△ABC中,AB的垂直平分线与BC交于点D,若AC=3,BC=4,则△ADC的周长为 .
 14. 如图,在中, , 以顶点为圆心,以适当长为半径画弧,分别交 , 于点、 , 再分别以点、为圆心,以大于的长为半径画弧,两弧交于点 , 作射线交边于点 , 若 , , 则的面积是.
14. 如图,在中, , 以顶点为圆心,以适当长为半径画弧,分别交 , 于点、 , 再分别以点、为圆心,以大于的长为半径画弧,两弧交于点 , 作射线交边于点 , 若 , , 则的面积是.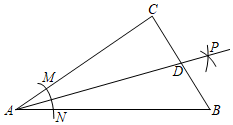 15. 已知 , 那么(ab)n=.16. 一副直角三角板如图放在直线、之间,且 , 则图中度.
15. 已知 , 那么(ab)n=.16. 一副直角三角板如图放在直线、之间,且 , 则图中度. 17.
17.如图,在正方形方格中,阴影部分是涂黑7个小正方形所形成的图案,再将方格内空白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法有种.
 18. 如图1,正方形的边上有一定点 , 连接.动点从正方形的顶点出发,沿以1cm/s的速度匀速运动到终点.图2是点运动时,的面积y(cm2)随时间x(s)变化的全过程图象,则的长度为cm.
18. 如图1,正方形的边上有一定点 , 连接.动点从正方形的顶点出发,沿以1cm/s的速度匀速运动到终点.图2是点运动时,的面积y(cm2)随时间x(s)变化的全过程图象,则的长度为cm. 19. 如图,在中, , 两锐角的角平分线交于点 , 点、分别在边、上,且都不与点重合,若 , 连接 , 当 , , 时,则的周长为.
19. 如图,在中, , 两锐角的角平分线交于点 , 点、分别在边、上,且都不与点重合,若 , 连接 , 当 , , 时,则的周长为.
三、解答题
-
20.(1)、计算:(2)、化简:21. 先化简,再求值: , 其中 , .22. 某客运公司的行李托运收费标准为:行李是1千克,收费为4元(不足1千克的按1千克计),以后每增加1千克需要增加相同的费用.
行李质量/千克
托运费/元
(1)、完成上面表格;(2)、写出行李托运费(元)与行李质量(千克)的关系式.23. 如图,点 , , , 在一直线上, , , .求证:.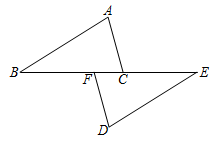 24. 在边长为1的小正方形组成的网格中(我们把组成网格的小正方形的顶点称为格点),的三个顶点都在格点上,请利用网格线和直尺画图.
24. 在边长为1的小正方形组成的网格中(我们把组成网格的小正方形的顶点称为格点),的三个顶点都在格点上,请利用网格线和直尺画图. (1)、在图中画出关于直线成轴对称的;(2)、求出的面积;(3)、在所给的网格内,在直线上找一点 , 使的面积等于的面积.25. 如图,已知四边形 ,连接 ,其中 , , ,延长 到点 ,得 ,点 为 上一点,连接 、 , 交 于点 .
(1)、在图中画出关于直线成轴对称的;(2)、求出的面积;(3)、在所给的网格内,在直线上找一点 , 使的面积等于的面积.25. 如图,已知四边形 ,连接 ,其中 , , ,延长 到点 ,得 ,点 为 上一点,连接 、 , 交 于点 . (1)、求证: ;(2)、若 , ,试探究 、 的数量关系,并说明理由;(3)、如图2,连接 ,若 ,求 的度数.26. 已知 , .(1)、当时,求的值;(2)、求的值.27. 已知A、B两地相距 米,甲、乙两人同时从A地出发前往B地,出发 分钟后,乙减慢了速度,最终比甲晚到,两人所走路程y(米)与行驶时间x(分)之间的关系如图所示,请回答下列问题:
(1)、求证: ;(2)、若 , ,试探究 、 的数量关系,并说明理由;(3)、如图2,连接 ,若 ,求 的度数.26. 已知 , .(1)、当时,求的值;(2)、求的值.27. 已知A、B两地相距 米,甲、乙两人同时从A地出发前往B地,出发 分钟后,乙减慢了速度,最终比甲晚到,两人所走路程y(米)与行驶时间x(分)之间的关系如图所示,请回答下列问题: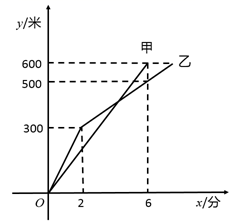 (1)、求甲的速度为多少米/分?(2)、求乙减慢速度后,路程y与行驶时间x之间的关系式?(3)、在甲到达B地前,求乙行驶多长时间时,甲、乙两人相距 米?28. 以为斜边在它的同侧作和 , 其中 , , 、交于点.
(1)、求甲的速度为多少米/分?(2)、求乙减慢速度后,路程y与行驶时间x之间的关系式?(3)、在甲到达B地前,求乙行驶多长时间时,甲、乙两人相距 米?28. 以为斜边在它的同侧作和 , 其中 , , 、交于点. (1)、如图1,平分 , 求证:;(2)、如图2,过点作 , 分别交、于点、点 , 连接 , 过作 , 交于点 , 连接 , 交于点 , 求证:;(3)、如图3,点为边的中点,点是边上一动点,连接 , 将线段绕点逆时针旋转得到线段 , 连接、 , 当 , 时,求的最小值.
(1)、如图1,平分 , 求证:;(2)、如图2,过点作 , 分别交、于点、点 , 连接 , 过作 , 交于点 , 连接 , 交于点 , 求证:;(3)、如图3,点为边的中点,点是边上一动点,连接 , 将线段绕点逆时针旋转得到线段 , 连接、 , 当 , 时,求的最小值.