四川省成都市高新区2020-2021学年七年级下学期期末数学试卷
试卷更新日期：2022-06-22 类型：期末考试
一、单选题
-
1. 计算（a4）2的结果是（ ）A、a6 B、a8 C、a16 D、a642. 下列图形中，可以被看作是轴对称图形的是（ ）A、
B、
C、
D、
3. 随着北斗系统全球组网的步伐，北斗芯片的研发生产技术也在逐步成熟，国产北斗芯片可支持接收多系统的导航信号，应用于自动驾驶、无人机、机器人等高精度定位需求领域，将为中国北斗导航产业发展提供有力支持．目前，该芯片工艺已达22纳米（即0.000000022米）．则数据0.000000022用科学记数法表示为（ ）A、0.22×10﹣7 B、2.2×10﹣8 C、22×10﹣9 D、22×10﹣104. 下列从左到右的变形，错误的是（ ）A、﹣m+n＝﹣（m+n） B、﹣a﹣b＝﹣（a+b） C、（m﹣n）3＝﹣（n﹣m）3 D、（y﹣x）2＝（x﹣y）25. 下列事件中，是必然事件的是（ ）A、任意掷一枚质地均匀的骰子，掷出的点数是奇数 B、一个射击运动员每次射击的命中环数 C、任意买一张电影票，座位号是2的倍数 D、早上的太阳从东方升起6. 如图，一个含有30°角的直角三角尺的两个顶点放在直尺的对边上.如果∠1＝20°，那么∠2的度数是（ ）
A、40° B、35° C、30° D、20°7. 等腰三角形一边长9cm，另一边长4cm，它的第三边是（ ）cm.A、4 B、9 C、4或9 D、大于5且小于138. 如图，在Rt△ABC中，BD是∠ABC的平分线，DE⊥AB，垂足是E.若AC＝5，DE＝2，则AD为（ ）
A、4 B、3 C、2 D、19. 如图，已知∠ABC＝∠DCB，要使△ABC≌△DCB，只需添加一个条件，这个条件不能是（ ）
A、∠A＝∠D B、∠ACB＝∠DBC C、AC＝BD D、AB＝DC10. 柿子熟了，从树上落下来.下面可以大致刻画出柿子下落过程（即落地前）的速度变化情况的是（ ）A、
B、
C、
D、
二、填空题
-
11. 如图，如果∠1＋∠2=280°，则∠3的度数是；
12. 已知am＝3，an＝5，则am+n的值为 ．13. 如图，小明站在堤岸的A点处，正对他的S点停有一艘游艇.他想知道这艘游艇距离他有多远，于是他沿堤岸走到电线杆B旁，接着再往前走相同的距离，到达C点.然后他向左直行，当看到电线杆与游艇在一条直线上时停下来，此时他位于D点.小明测得C、D间的距离为90米，则在A点处小明与游艇的距离为米.
14. 某商场将一商品在保持销售价80元/件不变的前提下，规定凡购买超过5件者，超出的部分打5折出售.若顾客购买x（x＞5）件，应付y元，则y与x间的关系式是.15. 已知m﹣n＝﹣1，mn＝5，则（3﹣m）（3+n）的值为.16. 如图是一个转盘，转盘上共有红、白两种不同的颜色，已知红色区域的圆心角为110°，自由转动转盘，指针落在白色区域的概率是.
17. 在非直角△ABC中，∠A＝50°，任意两条高所在的直线交于点P，连接BP，CP，则∠BPC的度数是.18. 任意选取四个连续自然数，将它们的积再加上1，其结果可以表示成一个自然数的平方形式.比如：10×11×12×13+1＝1312.类似的，将12×13×14×15+1表示成一个自然数的平方，则这个自然数是；一般地，若n为自然数，则n（n+1）（n+2）（n+3）+1可以表示成一个自然数的平方，这个自然数是.（用含n的代数式表示）19. 如图，点C，D分别是边∠AOB两边OA、OB上的定点，∠AOB＝20°，OC＝OD＝4.点E，F分别是边OB，OA上的动点，则CE+EF+FD的最小值是.
三、解答题
-
20.(1)、计算：；(2)、化简：（2x﹣y）（2x+y）+（x﹣y）（x+2y）.21. 先化简，再求值：[（x+1）（x+4）﹣（3x﹣2）2]÷x，其中x.22. 如图，点D、C在线段BF上，且BD＝CF，AB∥EF，AB＝EF，判定AC与DE的位置关系，并说明理由.
23. 小明有A，B，C，D四根细木棒，长度分别为a＝3cm，b＝5cm，c＝7cm，d＝9cm.(1)、他想钉一个三角形木框，他有哪几种选择呢？请列举出来；(2)、现随机抽取三根细木棒，求能组成三角形的概率.24. 某公交车每月的支出费用为4000元，票价为2元/人，设每月有x人乘坐该公交车每月收入与支出的差额为y元.(1)、请写出y与x的关系式；(2)、完成如表：x/人
500
1000
2000
3000
y/元
﹣3000
﹣1000
1000
(3)、根据每月乘客量x（人）的数量，试讨论该公交车的盈亏情况.25. 如图，点C为线段AB上一点，以线段AC为腰作等腰直角△ACD，∠ACD＝90°，点E为CD延长线上一点，且CE＝CB，连接AE，BD，点F为AE延长线上一点，连接BF，FD.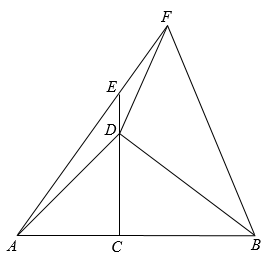
(1)、①求证：△ACE≌△DCB；②试判断BD与AF的位置关系，并证明；
(2)、若BD平分∠ABF，当CD＝3DE，S△ADE ， 求线段BF的长.26. 对于一个图形，通过两种不同的方法计算它的面积，可以得到一个数学等式.
(1)、如图1所示的大正方形，是由两个正方形和两个形状大小完全相同的长方形拼成的.用两种不同的方法计算图中阴影部分的面积，可以得到的数学等式是；(2)、如图2所示的大正方形，是由四个三边长分别为a、b、c的全等的直角三角形（a、b为直角边）和一个正方形拼成，试通过两种不同的方法计算中间正方形的面积，并探究a、b、c之间满足怎样的等量关系；(3)、利用（1）（2）的结论，如果直角三角形两直角边满足a+b＝17，ab＝60，求斜边c的值.27. 一艘货船在甲、乙两港之间承接往返运输任务.某日货船从甲港顺流出发，途经丙港并不做停留，抵达乙港停留一段时间后逆流返航.货船在行驶过程中保持自身船速（即船在静水中的速度）不变，已知水流速度为8千米/时，如图记录了当日这艘货船出发后与乙港的距离y（千米）随时间t（小时）的变化的图象.图象上的点A表示货船当日顺流航行到达丙港.
(1)、根据图象回答下列问题：货船在乙港停留的时间为小时，货船在静水中的速度为千米/时；(2)、m＝ ， n＝；(3)、货船当日顺流航行至丙港时，船上一救生圈不慎落入水中随水漂流，该货船能否在返航的途中找到救生圈？若能，请求出救生圈在水中漂流的时间；若不能，请说明理由.28. 已知△ABC≌△EDC，过点A作直线l∥BC；
(1)、如图1，点D在线段AC上时，点E恰好落在直线l上点A的右侧，求∠ACB的度数；(2)、如图2，在（1）的条件下，连接BE交AC于点F，G是线段CE上一点，且满足CG＝CF，连接DG交EF于点H，连接CH.求证：；(3)、如图3，∠ACB大小与（1）中相同，当点D不在线段AC上时，且点F、点G、点H满足（2）中条件，点M，N分别为线段CE，GD的延长线与直线l的交点.请直接写出△GMN为等腰三角形时，∠EBC与∠BCD满足的数量关系.