上海市徐汇区2022届高三下学期数学三模试卷

试卷更新日期：2022-06-22 类型：高考模拟

进入出卷网下载

一、填空题

1. 已知复数 $z_{1} = 1 + i$ ， $z_{2} = i$ （其中 $i$ 为虚数单位），则 $z_{1} \cdot z_{2} =$ .

查看试题解析
2. 已知集合 $A = {m | 1 < m < 4}$ ， $B = {y | y = x^{3} ， x \in R}$ ，则 $A ∩ B =$ .

查看试题解析
3. 设等差数列 ${a_{n}}$ 的前n项和为 $S_{n}$ ，若 $a_{2} + a_{8} = 15 - a_{5}$ ，则 $S_{9}$ 等于.

查看试题解析
4. 函数 $y = f (x)$ 的反函数为 $y = l o g_{2} x + 1$ ，则 $f (3) =$ .

查看试题解析
5. 已知 $c o s (\frac{π}{2} - α) = - \frac{4}{5}$ ，则 $c o s 2 α =$ .

查看试题解析
6. 已知多项式 ${(x - 1)}^{3} + {(x + 1)}^{4} = x^{4} + a_{1} x^{3} + a_{2} x^{2} + a_{3} x + a_{4}$ ，则 $a_{3} =$ .

查看试题解析
7. 《九章算术》是我国古代内容极为丰富的数学名著，第九卷“勾股”讲述了“勾股定理”及一些应用，其中直角三角形的三条边长分别称“勾”“股”“弦”，设点 $F$ 是抛物线 $y^{2} = 2 p x$ 的焦点，直线 $l$ 是该抛物线的准线，过抛物线上一点 $A$ 作准线的垂线 $A B$ ，垂足为 $B$ ，射线 $A F$ 交准线 $l$ 于点 $C$ ，若 $R t △ A B C$ 的“勾” $A B = 3$ ， “股” $C B = 3 \sqrt{3}$ ，则抛物线方程为.

查看试题解析
8. 某校航模队甲组有10名队员，其中4名女队员，乙组也有10名队员，其中6名女队员.现采用分层抽样（层内采用不放回随机抽样）从甲､乙两组中共抽取4名队员进行技术考核，则从乙组抽取的队员中恰有一名女队员的概率为.

查看试题解析
9. 设圆锥底面圆周上两点 $A$ 、 $B$ 间的距离为2，圆锥顶点到直线 $A B$ 的距离为 $\sqrt{3}$ ， $A B$ 和圆锥的轴的距离为1，则该圆锥的侧面积为.

查看试题解析
10. 设 $P_{n} (x_{n} ， y_{n})$ 是直线 $2 x - y = \frac{n}{n + 1} (n \in N^{*})$ 与圆 $x^{2} + y^{2} = 1$ 在第一象限的交点，则 $\underset{n \to \infty}{l i m} \frac{y_{n} - 1}{x_{n} - 1} =$ .

查看试题解析
11. 已知 $\vec{a}$ ､ $\vec{b}$ 是空间相互垂直的单位向量，且 $| \vec{c} | = 5$ ， $\vec{c} \cdot \vec{a} = \vec{c} \cdot \vec{b} = 2 \sqrt{2}$ ，则 $| \vec{c} - m \vec{a} - n \vec{b} |$ 的最小值是.

查看试题解析
12. 已知一簇双曲线 $E_{n}$ ： $x^{2} - y^{2} = {(\frac{n}{2022})}^{2} (n \in N^{*} ， n \leq 2022)$ ，设双曲线 $E_{n}$ 的左､右焦点分别为 $F_{n_{1}}$ ､ $F_{n_{2}}$ ， $P_{n}$ 是双曲线 $E_{n}$ 右支上一动点， $△ P_{n} F_{n_{1}} F_{n_{2}}$ 的内切圆 $G_{n}$ 与 $x$ 轴切于点 $A_{n} (a_{n} ， 0)$ ，则 $a_{1} + a_{2} + \cdot \cdot \cdot + a_{2022} =$ .

查看试题解析

二、单选题

13. 已知空间三条直线a､b､m及平面 $α$ ，且a､ $b$ $α$ ，条件甲： $m ⊥ a$ ， $m ⊥ b$ ；条件乙： $m ⊥ α$ ，则“条件乙成立”是“条件甲成立”的（）

A、充分非必要条件 B、必要非充分条件 C、充分且必要条件 D、既非充分也非必要条件

查看试题解析
14. 函数 $f (x) = (\frac{2}{1 + e^{x}} - 1) \sin x$ 图象的大致形状是（）

A、 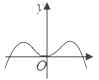B、 C、 D、

查看试题解析
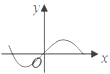15. 当曲线 $C_{1} ： {\begin{array}{l} x = 1 + c o s θ \\ y = s i n θ \end{array}$ ( $θ$ 为参数)的点到直线 $C_{2} ： {\begin{array}{l} x = t \cdot s i n 30 ° \\ y = 1 - t \cdot c o s 120 ° \end{array}$ (t为参数)的最短距离时，该点的坐标是（）.

A、 $(1 - \frac{\sqrt{2}}{2} ， - \frac{\sqrt{2}}{2})$ B、 $(1 - \frac{\sqrt{2}}{2} ， \frac{\sqrt{2}}{2})$ C、 $(- \frac{\sqrt{2}}{2} ， 1 - \frac{\sqrt{2}}{2})$ D、 $(\frac{\sqrt{2}}{2} ， 1 - \frac{\sqrt{2}}{2})$

查看试题解析
16. 已知函数 $f (x) = 2^{x}$ ， $g (x) = x^{2} + a x$ ，对于不相等的实数 $x_{1}$ 、 $x_{2}$ ，设 $m = \frac{f (x_{1}) - f (x_{2})}{x_{1} - x_{2}}$ ， $n = \frac{g (x_{1}) - g (x_{2})}{x_{1} - x_{2}}$ ，现有如下命题：
①对于任意的实数 $a$ ，存在不相等的实数 $x_{1}$ 、 $x_{2}$ ，使得m=n；②对于任意的实数 $a$ ，存在不相等的实数 $x_{1}$ 、 $x_{2}$ ，使得 $m = - n$ ，下列判断正确的是（）

A、①和②均为真命题 B、①和②均为假命题 C、①为真命题，②为假命题 D、①为假命题，②为真命题

查看试题解析

三、解答题

17. 如图，在正三棱住 $A B C - A_{1} B_{1} C_{1}$ 中， $A A_{1} = 4$ ，异面直线 $B C_{1}$ 与 $A A_{1}$ 所成角的大小为 $\frac{π}{3}$ ．

(1)、求正三棱柱 $A B C - A_{1} B_{1} C_{1}$ 的体积；

(2)、求直线 $B C_{1}$ 与平面 $A A_{1} C_{1} C$ 所成角的大小．（结果用反三角函数值表示）

查看试题解析
18. 已知函数 $f (x) = M s i n (ω x + φ) (ω > 0 ， 0 < φ < \frac{π}{2})$ 的部分图象如图所示.

(1)、求函数 $f (x)$ 的解析式；

(2)、在 $∠ A$ 为锐角的 $△ A B C$ 中，角 $A$ 、 $B$ 、 $C$ 的对边分别为 $a$ 、 $b$ 、 $c$ ，若 $f (\frac{A}{2}) = \frac{\sqrt{6} + \sqrt{2}}{2}$ ， $b + c = 2 + 3 \sqrt{2}$ ，且 $△ A B C$ 的面积为 $3$ ，求 $a$ 的值.

查看试题解析
19. 某油库的设计容量为30万吨，年初储量为10万吨，从年初起计划每月购进石油 $m$ 万吨，以满足区域内和区域外的需求，若区域内每月用石油1万吨，区域外前 $x$ 个月的需求量 $y$ （万吨）与 $x$ 的函数关系为 $y = \sqrt{2 p x} (p > 0 ， 1 \leq x \leq 16 ， x \in N^{*})$ ，并且前4个月，区域外的需求量为20万吨．

(1)、试写出第 $x$ 个月石油调出后，油库内储油量 $M$ （万吨）与 $x$ 的函数关系式；

(2)、要使16个月内每月按计划购进石油之后，油库总能满足区域内和区域外的需求，且每月石油调出后，油库的石油剩余量不超过油库的容量，试确定 $m$ 的取值范围．

查看试题解析
20. 已知椭圆 $M$ ： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 焦距为 $2 \sqrt{2}$ ，过点 $(\sqrt{2} ， \frac{\sqrt{3}}{3})$ ，斜率为 $k$ 的直线 $l$ 与椭圆有两个不同的交点 $A$ ､ $B$ .

(1)、求椭圆 $M$ 的方程；

(2)、若 $k = 1$ ， $| A B |$ 的最大值；

(3)、设 $P (- 2 ， 0)$ ，直线 $P A$ 与椭圆 $M$ 的另一个交点为 $C$ ，直线 $P B$ 与椭圆 $M$ 的另一个交点为 $D$ .若 $C$ ､ $D$ 和点 $Q (- \frac{7}{4} ， \frac{1}{2})$ 共线，求实数 $k$ 的值.

查看试题解析
21. 记实数 $a$ 、 $b$ 中较小者为 $m i n {a ， b}$ ，例如 $m i n {1 ， 2} = 1$ ， $m i n {1 ， 1} = 1$ ，对于无穷数列 ${a_{n}}$ ，记 $h_{k} = m i n {a_{2 k - 1} ， a_{2 k}}$ .若对任意 $k \in N^{*}$ 均有 $h_{k} < h_{k + 1}$ ，则称数列 ${a_{n}}$ 为“趋向递增数列”.

(1)、已知数列 ${a_{n}}$ 、 ${b_{n}}$ 的通项公式分别为 $a_{n} = c o s \frac{n π}{2}$ ， $b_{n} = {(- \frac{1}{2})}^{n}$ ，判断数列 ${a_{n}}$ 、 ${b_{n}}$ 是否为“趋向递增数列”？并说明理由；

(2)、已知首项为1，公比为 $q$ 的等比数列 ${c_{n}}$ 是“趋向递增数列”，求公比 $q$ 的取值范围；

(3)、若数列 ${d_{n}}$ 满足 $d_{1}$ 、 $d_{2}$ 为正实数，且 $d_{n} = | d_{n + 2} - d_{n + 1} |$ ，求证：数列 ${d_{n}}$ 为“趋向递增数列”的必要非充分条件是 ${d_{n}}$ 中没有0.

查看试题解析