山东省潍坊市2022届高三下学期数学三模统考（5月）试卷

试卷更新日期：2022-06-22 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知集合 $A$ ， $B$ ，若 $A = {- 1 ， 1}$ ， $A ∪ B = {- 1 ， 0 ， 1}$ ，则一定有（）

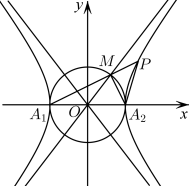
A、 $A \subseteq B$ B、 $B \subseteq A$ C、 $A ∩ B = \emptyset$ D、 $0 \in B$

查看试题解析
2. 已知复数 $z$ 满足 $(i - 1) z = 1 + i$ ，其中i是虚数单位，则 $\bar{z}$ 的虚部为（）

A、-1 B、1 C、0 D、2

查看试题解析
3. 某省新高考改革方案推行“ $3 + 1 + 2$ ”模式，要求学生在语数外3门全国统考科目之外，在历史和物理2门科目中必选且只选1门，再从化学、生物、地理、思想政治4门科目中任选2门．某学生各门功课均比较优异，因此决定按方案要求任意选择，则该生选考物理、生物和政治这3门科目的概率为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{6}$ D、 $\frac{1}{12}$

查看试题解析
4. 已知 $\vec{a}$ ， $\vec{b}$ 是平面内两个不共线的向量， $\vec{A B} = \vec{a} + λ \vec{b}$ ， $\vec{A C} = μ \vec{a} + \vec{b}$ ， $λ$ ， $μ \in R$ ，则 $A$ ， $B$ ， $C$ 三点共线的充要条件是（）

A、 $λ - μ = 1$ B、 $λ + μ = 2$ C、 $λ μ = 1$ D、 $\frac{λ}{μ} = 1$

查看试题解析
5. 我国古代数学名著《九章算术》中给出了很多立体几何的结论，其中提到的多面体“鳖臑”是四个面都是直角三角形的三棱锥．若一个“鳖臑”的所有顶点都在球 $O$ 的球面上，且该“鳖臑”的高为 $2$ ，底面是腰长为 $2$ 的等腰直角三角形．则球 $O$ 的表面积为（）

A、12π B、 $4 \sqrt{3} π$ C、6π D、 $2 \sqrt{6} π$

查看试题解析
6. 设函数 $f (x) = | s i n x |$ ，若 $a = f (l n 2)$ ， $b = f (l o g_{\frac{1}{3}} 2)$ ， $c = f (3^{\frac{1}{2}})$ ，则（）

A、 $a < b < c$ B、 $b < c < a$ C、 $c < a < b$ D、 $b < a < c$

查看试题解析
7. 已知双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左，右顶点分别是 $A_{1}$ ， $A_{2}$ ，圆 $x^{2} + y^{2} = a^{2}$ 与 $C$ 的渐近线在第一象限的交点为 $M$ ，直线 $A_{1} M$ 交 $C$ 的右支于点 $P$ ，若△ $M P A_{2}$ 是等腰三角形，且 $∠ P A_{2} M$ 的内角平分线与 $y$ 轴平行，则 $C$ 的离心率为（）

A、2 B、 $\sqrt{2}$ C、 $\sqrt{3}$ D、 $\sqrt{5}$

查看试题解析
8. 过点 $P (1 ， m) (m \in R)$ 有 $n$ 条直线与函数 $f (x) = x e^{x}$ 的图像相切，当 $n$ 取最大值时， $m$ 的取值范围为（）

A、 $- \frac{5}{e^{2}} < m < e$ B、 $- \frac{5}{e^{2}} < m < 0$ C、 $- \frac{1}{e} < m < 0$ D、 $m < e$

查看试题解析

二、多选题

9. 已知等差数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，等比数列 ${b_{n}}$ 的前 $n$ 项和为 $T_{n}$ ，则下列结论正确的是（）

A、数列 ${\frac{S_{n}}{n}}$ 为等差数列 B、对任意正整数 $n$ ， $b_{n}^{2} + b_{n + 2}^{2} \geq 2 b_{n + 1}^{2}$ C、数列 ${S_{2 n + 2} - S_{2 n}}$ 一定是等差数列 D、数列 ${T_{2 n + 2} - T_{2 n}}$ 一定是等比数列

查看试题解析
10. 已知定义域为R的函数 $f (x)$ 满足 $f (1 + x) + f (1 - x) = 0$ ，函数 $g (x) = f (x) s i n ω x (ω > 0)$ ，若函数 $y = g (x + 1)$ 为奇函数，则 $ω$ 的值可以为（）

A、 $\frac{π}{4}$ B、 $\frac{π}{2}$ C、π D、 $\frac{3 π}{2}$

查看试题解析
11. 函数 $f (x) = \sqrt{2} s i n (ω x + φ) (0 < ω \leq 2 ， - \frac{π}{2} < φ < \frac{3 π}{2})$ 的部分图像如图所示，则下列结论正确的是（）

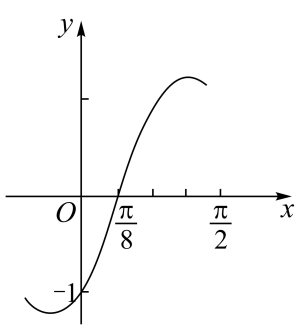A、 $φ = - \frac{π}{4}$ 或 $\frac{5 π}{4}$ B、 $f (x) = \sqrt{2} c o s (2 x - \frac{3 π}{4})$ C、 $f (\frac{π}{12}) = \frac{1 - \sqrt{3}}{2}$ D、若 $α \in (0 ， \frac{π}{2})$ 且 $f (α) > 0$ ，则 $s i n (α - \frac{π}{8}) < 0$

查看试题解析
12. 定义平面向量的一种运算“ $Θ$ ”如下：对任意的两个向量 $\vec{a} = (x_{1} ， y_{1})$ ， $\vec{b} = (x_{2} ， y_{2})$ ，令 $\vec{a} Θ \vec{b} = (x_{1} y_{2} - x_{2} y_{1} ， x_{1} x_{2} + y_{1} y_{2})$ ，下面说法一定正确的是（）

A、对任意的 $λ \in R$ ，有 $(λ \vec{a}) Θ \vec{b} = λ (\vec{a} Θ \vec{b})$ B、存在唯一确定的向量 $\vec{e}$ 使得对于任意向量 $\vec{a}$ ，都有 $\vec{a} Θ \vec{e} = \vec{e} Θ \vec{a} = \vec{a}$ 成立 C、若 $\vec{a}$ 与 $\vec{b}$ 垂直，则 $(\vec{a} Θ \vec{b}) Θ \vec{c}$ 与 $\vec{a} Θ (\vec{b} Θ \vec{c})$ 共线 D、若 $\vec{a}$ 与 $\vec{b}$ 共线，则 $(\vec{a} Θ \vec{b}) Θ \vec{c}$ 与 $\vec{a} Θ (\vec{b} Θ \vec{c})$ 的模相等

查看试题解析

三、填空题

13. 为了解某社区居民的2019年家庭年收入与年支出的关系，随机调查了该社区5户家庭，得到如下统计数据表：

收入x（万元）

8.2

8.6

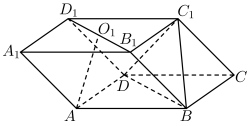
10.0

11.3

11.9

支出y（万元）

6.2

7.5

8.0

t

9.8

根据上表可得回归直线方程 $\hat{y} = 0.76 x + 0.4$ ，则t＝．

查看试题解析
14. 已知 $F$ 是抛物线 $y^{2} = 2 p x (p > 0)$ 的焦点，过 $F$ 作两条互相垂直的直线 $l_{1}$ ， $l_{2}$ ，直线 $l_{1}$ 交抛物线于 $A$ ， $B$ 两点，直线 $l_{2}$ 交抛物线于 $C$ ， $D$ 两点，且 $| A B | \cdot | C D |$ 的最小值是64，则抛物线的方程为．

查看试题解析
15. 已知函数 $f (x) = c o s 2 x$ 向右平移 $\frac{π}{12}$ 个单位长度后得到 $g (x)$ ．若对于任意的 $x_{1} \in [- \frac{π}{3} ， \frac{π}{6}]$ ，总存在 $x_{2} \in [m ， n]$ ，使得 $f (x_{1}) = g (x_{2})$ ，则 $| m - n |$ 的最小值为．

查看试题解析
16. 已知正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的棱长为1，空间一动点 $P$ 满足 $A_{1} P ⊥ A B_{1}$ ，且 $∠ A P B_{1} = ∠ A D B_{1}$ ，则 $t a n ∠ A P B_{1} =$ ，点 $P$ 的轨迹围成的封闭图形的面积为．

查看试题解析

四、解答题

17. 在①数列 ${a_{n}}$ 为等差数列，且 $a_{1} = 1$ ， $a_{n + 1} = 2 a_{n} - (2 n - 3)$ ， ② $a_{1} = 2$ ， $2 S_{n} = (n + 1) a_{n}$ ，
③正项数列 ${a_{n}}$ 满足 $4 S_{n} = a_{n}^{2} + 2 a_{n} - 3$ 这三个条件中任选一个，补充在下面问题中，并给出解答．
问题：已知数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，且____？
注：如果选择多个条件分别解答，按第一个解答计分．

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、若数列 ${{(- 1)}^{n} \cdot a_{n}}$ 的前 $n$ 项和为 $T_{n}$ ，求 $T_{2 n}$ ．

查看试题解析
18. 已知 $△ A B C$ 的内角 $A$ ， $B$ ， $C$ 的对边分别为 $a$ ， $b$ ， $c$ ，且 $2 a s i n (C + \frac{π}{6}) = b + c$ ．

(1)、求角 $A$ 的大小；

(2)、若 $a = \sqrt{7}$ ， $\vec{B A} \cdot \vec{A C} = - 3$ ， $∠ A$ 的平分线交边 $B C$ 于点 $T$ ，求 $A T$ 的长．

查看试题解析
19. 盲盒，是指消费者不能提前得知具体产品款式的玩具盒子，具有随机性．因其独有的新鲜性，刺激性及社交属性而深受各个年龄段人们的喜爱．已知 $M$ 系列盲盒共有12个款式，为调查 $M$ 系列盲盒更受哪个年龄段的喜爱，向00前、00后人群各随机发放了50份问卷，并全部收回．经统计，有45%的人未购买该系列育盒，在这些未购买者当中，00后占 $\frac{2}{3}$ ．

(1)、请根据以上信息填表，并分析是否有99%的把握认为购买该系列盲盒与年龄有关？

00前
00后
总计
购买
未购买
总计
100
附： $K^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，
$P (K^{2} \geq k_{0})$
0.10
0.05
0.010
0.001
$k_{0}$
2.706
3.841
6.635
10.828

(2)、一批盲盒中，每个盲盒随机装有一个款式，甲同学已经买到3个不同款，乙、丙同学分别已经买到 $m$ 个不同款，已知三个同学各自新购买一个盲盒，且相互之间无影响，他们同时买到各自的不同款的概率为 $\frac{1}{3}$ ．
①求 $m$ ；
②设 $X$ 表示三个同学中各买到自己不同款的总人数，求 $X$ 的分布列和数学期望．

查看试题解析
20. 如图所示，已知平行六面体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，侧面 $C D D_{1} C_{1} ⊥$ 底面 $A B C D$ ， $A B = A D = 2$ ， $∠ B A D = \frac{π}{3}$ ， $∠ A_{1} A B = \frac{3 π}{4}$ ， $O_{1}$ 为线段 $B_{1} D_{1}$ 的中点．

(1)、证明： $A O_{1} ∥$ 平面 $C_{1} B D$ ；

(2)、已知二面角 $B - C_{1} D - C$ 的余弦值为 $\frac{\sqrt{7}}{7}$ ，求直线 $A_{1} C$ 与平面 $C_{1} B D$ 所成角的正弦值．

查看试题解析
21. 已知 $O$ 为坐标原点，定点 $F (1 ， 0)$ ， $M$ 是圆 $O ： x^{2} + y^{2} = 4$ 内一动点，圆 $O$ 与以线段 $F M$ 为直径的圆内切．

(1)、求动点 $M$ 的轨迹方程；

(2)、若直线 $l$ 与动点 $M$ 的轨迹交于 $P$ ， $Q$ 两点，以坐标原点 $O$ 为圆心，1为半径的圆与直线 $l$ 相切，求△ $P O Q$ 面积的最大值．

查看试题解析
22. 已知函数 $f (x) = e^{x} (1 + a l n x)$ ．

(1)、当 $f (x)$ 有两个极值点时，求 $a$ 的取值范围；

(2)、若 $a \geq \frac{3}{2}$ ，且函数 $f (x)$ 的零点为 $x_{1}$ ，证明：导函数 $f^{'} (x)$ 存在极小值点，记为 $x_{2}$ ，且 $x_{1} > x_{2}$ ．

查看试题解析

收入x（万元）	8.2	8.6	10.0	11.3	11.9
支出y（万元）	6.2	7.5	8.0	t	9.8

$P (K^{2} \geq k_{0})$	0.10	0.05	0.010	0.001
$k_{0}$	2.706	3.841	6.635	10.828

	00前	00后	总计
购买
未购买
总计			100