广东省深圳市南山区2020-2021学年八年级下学期期末数学试题

试卷更新日期：2022-06-21 类型：期末考试

进入出卷网下载

一、单选题

1. 使分式 $\frac{m - 1}{m - 3}$ 在实数范围内有意义，则实数m的取值范围是（　　）

A、m≠1 B、m≠3 C、m＝3 D、m＝1

查看试题解析
2. 下列图形中，是轴对称图形不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列实数中，能够满足不等式 $x - 3 < 0$ 的正整数是（）

A、-2 B、3 C、4 D、2

查看试题解析
4. 若 $x < y$ ，则下列不等式成立的是（）

A、 $3 x > 3 y$ B、 $x + 1 < y + 1$ C、 $\frac{x}{3} > \frac{y}{3}$ D、 $- \frac{x}{3} < - \frac{y}{3}$

查看试题解析
5. 设四边形的内角和等于a，五边形的内角和等于b，则a与b的关系是（　　）

A、a＞b B、a＝b C、a＝b+180° D、b＝a+180°

查看试题解析
6. 若 $\frac{a}{b} = 2$ ，则 $\frac{a^{2} - a b}{a^{2} - b^{2}}$ 的值为（）

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、 $- \frac{1}{3}$ D、 $- \frac{2}{3}$

查看试题解析
7. 平行四边形的两条对角线一定（）

A、互相平分 B、互相垂直 C、相等 D、以上都不对

查看试题解析
8. 阅读理解：我们把 $| \begin{matrix} a \\ c \end{matrix} \begin{matrix} b \\ d \end{matrix} |$ 称作二阶行列式，规定它的运算法则为 $| \begin{matrix} a \\ c \end{matrix} \begin{matrix} b \\ d \end{matrix} |$ =ad﹣bc，例如 $| \begin{matrix} 1 \\ 2 \end{matrix} \begin{matrix} 3 \\ 4 \end{matrix} |$ =1×4﹣2×3=﹣2，如果 $| \begin{matrix} 2 \\ 1 \end{matrix} \begin{matrix} 3 - x \\ x \end{matrix} |$ ＞0，则x的解集是（）

A、x＞1 B、x＜﹣1 C、x＞3 D、x＜﹣3

查看试题解析
9. 如图， $R t △ A B C$ 中， $∠ C = 90 °$ ， $A D$ 平分 $∠ B A C$ ，交 $B C$ 于点D， $A B = 18$ ， $S_{△ A B D} = 27$ ，则 $C D$ 的长为（）

A、4 B、8 C、3 D、6

查看试题解析
10. 如图，将一个含30°角的直角三角尺 $A O B$ 放在平面直角坐标系中，两条直角边分别与坐标轴重叠．已知 $∠ O A B = 30 °$ ， $A B = 16$ ，点D为斜边 $A B$ 的中点，现将三角尺 $A O B$ 绕点O顺时针旋转90°，则点D的对应点 $D^{'}$ 的坐标为（）

A、 $(4 \sqrt{3} ， 4)$ B、 $(8 \sqrt{3} ， - 8)$ C、 $(4 ， - 4 \sqrt{3})$ D、 $(4 \sqrt{3} ， - 4)$

查看试题解析

二、填空题

11. 因式分解： $a^{2} - 4 b^{2}$ = ．

查看试题解析
12. 如果若分式 $\frac{a^{2} - 9}{a - 3}$ 的值为0，则实数a的值为.

查看试题解析
13. 如图，平行四边形 $A B C D$ 中， $A B = 9$ ， $B C = 4$ ，连接 $A C$ ，分别以点A和点C为圆心，大于 $\frac{1}{2} A C$ 的长为半径作弧，两弧相交于点M，N，作直线 $M N$ ，交 $C D$ 于点E，连接 $A E$ ，则 $△ A E D$ 的周长是．

查看试题解析
14. 如图，直线 $y_{1} = x + b$ 与 $y_{2} = k x - 1$ 相交于点P，则关于x的不等式 $x + b > k x - 1$ 的解集为．

查看试题解析
15. 如图，在四边形 $A B C D$ 中， $A D = B C$ ，点P是对角线的中点，点E和点F分别是 $A B$ 与 $C D$ 的中点．若 $∠ P E F = 20 °$ ，则 $∠ E P F$ 的度数是．

查看试题解析

三、解答题

16. 解不等式（组）

(1)、解不等式： $1 - \frac{x + 2}{3} > - \frac{x}{6}$ ，并把解集在数轴上表示出来．

(2)、求不等式组 ${\begin{array}{l} 5 x - 1 > 3 (x + 1) \\ \frac{1}{2} x - 1 \leq 7 - \frac{3}{2} x \end{array}$ 的正整数解．

查看试题解析
17. 先化简，再求值： $(a - \frac{3 a}{a + 1}) \div \frac{a - 2}{a^{2} + 2 a + 1}$ 请选择一个合适的数作为a值求式子的值．

查看试题解析
18. 解分式方程： $\frac{2}{x^{2} - 4}$ + $\frac{x}{x - 2}$ ＝1．

查看试题解析
19. 如图， $△ A B C$ 的三个顶点都在边长为1的小正方形组成的网格的格点上，以点 $O$ 为原点建立直角坐标系，回答下列问题：
（ 1 ）将 $△ A B C$ 先向上平移5个单位，再向右平移1个单位得到 $△ A_{1} B_{1} C_{1}$ ，画出 $△ A_{1} B_{1} C_{1}$ ，并直接写出 $A_{1}$ 的坐标；
（ 2 ）将 $△ A_{1} B_{1} C_{1}$ 绕点 $(0 ， - 1)$ 顺时针旋转90°得到 $△ A_{2} B_{2} C_{2}$ ，画出 $△ A_{2} B_{2} C_{2}$ ；
（ 3 ）观察图形发现， $△ A_{2} B_{2} C_{2}$ 是由 $△ A B C$ 绕点 ▲ （写出点的坐标）顺时针旋转 ▲ 度得到的．

查看试题解析
20. 如图，分别以 $R t △ A B C$ 的直角边 $A C$ 及斜边 $A B$ 向外作等边 $△ A C D$ ，等边 $△ A B E$ ，已知 $∠ B A C = 30 °$ ， $E F ⊥ A B$ ，垂足为F，连接 $D F$

(1)、求证： $△ A E F ≌ △ B A C$ ；

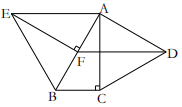(2)、四边形 $A D F E$ 是平行四边形吗？请说明理由．

查看试题解析
21. 五月的第二个星期日是母亲节，母亲们在这一天通常会收到礼物，康乃馨被视为献给母亲的花，某花店在母亲节前夕用3000元购进一批康乃馨，在母亲节当天供不应求，又马上用6000元加急购进一批康乃馨，第二批康乃馨数量是第一批的1.2倍，单价比第一批贵2元．

(1)、第一批康乃馨进货单价多少元？

(2)、若两次购进康乃馨按同一价格销售，两批全部售完后，获利不少于4200元，那么销售价至少为多少元？

查看试题解析
22. 在平行四边形 $A B C D$ 中， $A B ⊥ C D$ 于E， $C F ⊥ A D$ 于F，H为 $A D$ 上一动点，连接 $C H$ ， $C H$ 交 $A E$ 于 $G$ ，且 $A E = C D = 4$ ．

(1)、如图1，若 $∠ B = 60 °$ ，求 $C F$ 、 $A F$ 的长；

(2)、如图2，当 $F H = F D$ 时，求证： $C G = E D + A G$ ；

(3)、如图3，若 $∠ B = 60 °$ ，点H是直线 $A D$ 上任一点，将线段 $C H$ 绕C点逆时针旋转60°，得到线段 $C H^{'}$ ，请直接写出 $A H^{'}$ 的最小值．

查看试题解析