山东省青州市2022届高三下学期数学打靶试卷

试卷更新日期：2022-06-21 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知集合 $M = {x | - 1 \leq x \leq 2}$ ， $N = {x | y = l n x}$ ，则 $M ∩ N =$ （）

A、 $[- 1 ， 2]$ B、 $(- 1 ， 2]$ C、 $(0 ， 2]$ D、 $(- \infty ， - 1) ∪ [2 ， + \infty)$

查看试题解析
2. 复数 $z$ 满足 $z (1 + i) = | 1 - \sqrt{3} i |$ ，则复数 $z =$ （）

A、 $\sqrt{2} (c o s \frac{π}{4} + i s i n \frac{π}{4})$ B、 $\sqrt{2} (c o s \frac{π}{4} - i s i n \frac{π}{4})$ C、 $\sqrt{2} (c o s \frac{3 π}{4} + i s i n \frac{3 π}{4})$ D、 $\sqrt{2} (c o s \frac{7 π}{4} - i s i n \frac{7 π}{4})$

查看试题解析
3. 定义： $| \vec{a} \times \vec{b} | = | \vec{a} | | \vec{b} | s i n θ$ ，其中 $θ$ 为向量 $\vec{a}$ 与 $\vec{b}$ 的夹角．若 $| \vec{a} | = 2$ ， $| \vec{b} | = 5$ ， $\vec{a} \cdot \vec{b} = - 6$ ，则 $| \vec{a} \times \vec{b} |$ 等于（）

A、6 B、-6 C、-8 D、8

查看试题解析
4. 已知双曲线C的顶点为 $A_{1}$ ， $A_{2}$ ，虚轴的一个端点为B，且 $△ B A_{1} A_{2}$ 是一个等边三角形，则双曲线C的离心率为（）

A、2 B、 $\sqrt{2}$ C、3 D、 $\sqrt{3}$

查看试题解析
5. 函数 $f (x) = A s i n (ω x + φ) (A > 0 ， ω > 0 ， | φ | < \frac{π}{2})$ 的部分图像如图所示，现将 $f (x)$ 的图像向左平移 $\frac{π}{6}$ 个单位长度，得到函数 $g (x)$ 的图像，则 $g (x)$ 的表达式可以为（）

A、 $g (x) = 2 s i n 2 x$ B、 $g (x) = 2 c o s (2 x - \frac{π}{3})$ C、 $g (x) = 2 s i n (x - \frac{π}{6})$ D、 $g (x) = 2 c o s (x + \frac{π}{3})$

查看试题解析
6. Poisson分布是统计学里常见的离散型概率分布，由法国数学家西莫恩·德尼·泊松首次提出，Poisson分布的概率分布列为 $P (X = K) = \frac{λ^{k}}{k!} e^{- λ} (k = 0 ， 1 ， 2 ， \cdot \cdot \cdot)$ ，其中 $e$ 为自然对数的底数， $λ$ 是Poisson分布的均值．当二项分布的n很大 $(n \geq 20)$ 而p很小 $(p \leq 0.05)$ 时，Poisson分布可作为二项分布的近似．假设每个大肠杆菌基因组含有10000个核苷酸对，采用 $0.05 J / m^{2}$ 紫外线照射大肠杆菌时，每个核苷酸对产生嘧啶二体的概率均为0.0003，已知该菌株基因组有一个嘧啶二体就致死，则致死率是（）

A、 $1 - e^{- 3}$ B、 $e^{- 3}$ C、 $1 - 3 e^{- 3}$ D、 $1 - 4 e^{- 3}$

查看试题解析
7. 学校手工课上同学们分组研究正方体的表面展开图．某小组得到了如图所示表面展开图，则在正方体中， $A B$ 、 $C D$ 、 $E F$ 、 $G H$ 这四条线段所在的直线中，异面直线有（）

A、1对 B、3对 C、5对 D、2对

查看试题解析
8. 设 $a = \frac{4 - l n 4}{e^{2}}$ ， $b = \frac{l n 2}{2}$ ， $c = \frac{1}{e}$ ，则（）

A、 $a < c < b$ B、 $a < b < c$ C、 $b < a < c$ D、 $b < c < a$

查看试题解析

二、多选题

9. 为响应自己城市倡导的低碳出行，小李上班可以选择公交车、自行车两种交通工具，他分别记录了100次坐公交车和骑车所用时间（单位：分钟），得到下列两个频率分布直方图：基于以上统计信息，则正确的是（）

A、骑车时间的中位数的估计值是22分钟 B、骑车时间的众数的估计值是21分钟 C、坐公交车时间的40%分位数的估计值是19分钟 D、坐公交车时间的平均数的估计值小于骑车时间的平均数的估计值

查看试题解析
10. 已知定义域为 $I$ 的偶函数 $f (x)$ 在 $(0 ， + ∞)$ 上单调递增，且 $\exists x_{0} \in I$ ，使 $f (x_{0}) < 0$ ．则下列函数中符合上述条件的是（）

A、 $f (x) = x^{2} - 3$ B、 $f (x) = 2^{x} + 2^{- x}$ C、 $f (x) = l o g_{2} | x |$ D、 $f (x) = c o s x + 1$

查看试题解析
11. 过抛物线 $C ： y^{2} = 2 p x$ 上一点 $A (1 ， - 4)$ 作两条相互垂直的直线，与 $C$ 的另外两个交点分别为 $M$ ， $N$ ，则（）

A、 $C$ 的准线方程是 $x = - 4$ B、过 $C$ 的焦点的最短弦长为8 C、直线 $M N$ 过定点 $(0 ， 4)$ D、当点 $A$ 到直线 $M N$ 的距离最大时，直线 $M N$ 的方程为 $2 x + y - 38 = 0$

查看试题解析
12. 已知数列 ${a_{n}}$ 的前n项和为 $S_{n}$ ， $a_{1} = 1$ ，且 $4 a_{n} \cdot a_{n + 1} = a_{n} - 3 a_{n + 1}$ （ $n = 1$ ， 2，…），则（）

A、 $3 a_{n + 1} < a_{n}$ B、 $a_{5} = \frac{1}{243}$ C、 $l n (\frac{1}{a_{n}}) < n + 1$ D、 $1 \leq S_{n} < \frac{17}{14}$

查看试题解析

三、填空题

13. ${(2 x - \frac{1}{x})}^{6}$ 的展开式中的常数项为．

查看试题解析
14. 在平面直角坐标系xOy中，角α与角β均以Ox为始边，它们的终边关于直线 $y = x$ 对称.若 $\sin α = \frac{1}{3}$ ，则 $\sin (α - β) =$ .

查看试题解析
15. 已知 $f (x) = e^{x} - 1$ （ $e$ 为自然对数的底数）， $g (x) = l n x + 1$ ，请写出 $f (x)$ 与 $g (x)$ 的一条公切线的方程．

查看试题解析
16. 如图，将正四面体每条棱三等分，截去顶角所在的小正四面体，余下的多面体就成为一个半正多面体，亦称“阿基米德体”．点A，B，M是该多面体的三个顶点，点N是该多面体外接球表面上的动点，且总满足 $M N ⊥ A B$ ，若 $A B = 4$ ，则该多面体的表面积为；点N轨迹的长度为．

查看试题解析

四、解答题

17. 已知公差为正数的等差数列 ${a_{n}}$ ， $a_{2}$ 与 $a_{8}$ 的等差中项为8，且 $a_{3} a_{7} = 28$ ．

(1)、求 ${a_{n}}$ 的通项公式；

(2)、从 ${a_{n}}$ 中依次取出第1项、第3项、第9项、…、第 $3^{n - 1}$ 项，按照原来的顺序组成一个新数列 ${b_{n}}$ ，求数列 ${b_{n}}$ 的前 $n$ 项和 $S_{n}$ ．

查看试题解析
18. 在 $△ A B C$ 中，内角 $A ， B ， C$ 的对边分别为 $a ， b ， c$ ， $b t a n A + b t a n B = \frac{\sqrt{3} c}{c o s A}$ ．

(1)、求角 $B$ ；

(2)、 $D$ 是 $A C$ 边上的点，若 $C D = 1$ ， $A D = B D = 3$ ，求 $s i n A$ 的值．

查看试题解析
19. 新冠肺炎疫情发生以来，我国某科研机构开展应急科研攻关，研制了一种新型冠状病毒疫苗，并已进入二期临床试验．根据普遍规律，志愿者接种疫苗后体内会产生抗体，人体中检测到抗体，说明有抵御病毒的能力．通过检测，用x表示注射疫苗后的天数，y表示人体中抗体含量水平（单位：miu/mL，即：百万国际单位/毫升），现测得某志愿者的相关数据如下表所示．
天数x
1
2
3
4
5
6
抗体含量水平y
5
10
26
50
96
195
根据以上数据，绘制了散点图．
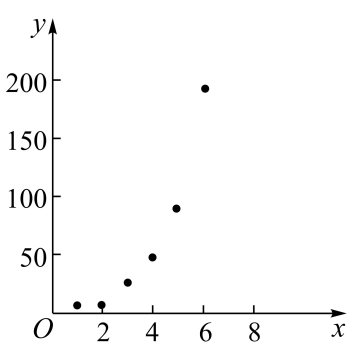
参考数据：其中 $w = l n y$ ．
$\bar{x}$
$\bar{y}$
$\bar{w}$
$\sum_{i = 1}^{6} {(x_{i} - \bar{x})}^{2}$
$\sum_{i = 1}^{6} {(w_{i} - \bar{w})}^{2}$
$\sum_{i = 1}^{6} (w_{i} - \bar{w}) (x_{i} - \bar{x})$
$\sum_{i = 1}^{6} (x_{i} - \bar{x}) (y_{i} - \bar{y})$
$e^{8.3}$
3.50
63.67
3.49
17.50
9.49
12.95
519.01
4023.87
参考公式：； $\hat{b} = \frac{\sum_{i = 1}^{n} (u_{i} - \bar{u}) (v_{i} - \bar{v})}{\sum_{i = 1}^{n} {(u_{i} - \bar{u})}^{2}} = \frac{\sum_{i = 1}^{n} u_{i} v_{i} - n \bar{u} \bar{v}}{\sum_{i = 1}^{n} {u_{i}}^{2} - n {\bar{u}}^{2}}$ ， $\hat{a} = \bar{v} - \hat{b} \bar{u}$ ．

(1)、根据散点图判断， $y = c \cdot e^{d x}$ 与 $y = a + b x$ （a，b，c，d均为大于0的实数）哪一个更适宜作为描述y与x关系的回归方程类型？（给出到断即可，不必说明理由）

(2)、根据（1）的判断结果求出y关于x的回归方程，并预测该志愿者在注射疫苗后的第10天的抗体含量水平值；

(3)、从这位志愿者的前6天的检测数据中随机抽取3天的数据作进一步的分析，求其中的y值小于50的天数 $X$ 的分布列及数学期望．

查看试题解析
20. 如图，四棱锥 $P - A B C D$ 中，底面ABCD是矩形， $P A ⊥$ 平面ABCD， $A B = 1 ， A D = 2$ ，点F是棱BC的中点.

(1)、若PB与平面ABCD所成的角为 $45 °$ ，求二面角 $A - P F - C$ 的大小；

(2)、若直线PB与过直线AF的平面 $α$ 平行，平面 $α$ 与棱PD交于点S，指明点 $S$ 的位置，并证明.

查看试题解析
21. 已知双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左、右焦点分别为 $F_{1}$ 、 $F_{2}$ ，双曲线 $C$ 的右顶点 $A$ 在圆 $O ： x^{2} + y^{2} = 3$ 上，且 $\vec{A F_{1}} \cdot \vec{A F_{2}} = - 1$ ．

(1)、求双曲线 $C$ 的方程；

(2)、动直线 $l$ 与双曲线 $C$ 恰有1个公共点，且与双曲线 $C$ 的两条渐近线分别交于点 $M$ 、 $N$ ，设 $O$ 为坐标原点．求证： $△ O M N$ 的面积为定值．

查看试题解析
22. 已知函数 $f (x) = l n (1 + x) - \frac{2 x}{2 + x + a x^{2}} (a \in R)$ ．

(1)、若 $a = 0$ ，证明：当 $- 1 < x < 0$ 时， $f (x) < 0$ ；当 $x > 0$ 时， $f (x) > 0$ ；

(2)、若 $x = 0$ 是 $f (x)$ 的极大值点，求实数a．

查看试题解析

$\bar{x}$	$\bar{y}$	$\bar{w}$	$\sum_{i = 1}^{6} {(x_{i} - \bar{x})}^{2}$	$\sum_{i = 1}^{6} {(w_{i} - \bar{w})}^{2}$	$\sum_{i = 1}^{6} (w_{i} - \bar{w}) (x_{i} - \bar{x})$	$\sum_{i = 1}^{6} (x_{i} - \bar{x}) (y_{i} - \bar{y})$	$e^{8.3}$
3.50	63.67	3.49	17.50	9.49	12.95	519.01	4023.87

天数x	1	2	3	4	5	6
抗体含量水平y	5	10	26	50	96	195