2012年高考理数真题试卷（江苏卷）

试卷更新日期：2016-09-23 类型：高考真卷

进入出卷网下载

一、填空题：请把答案填写在答题卡相应位置上．

1. 已知集合A={1，2，4}，B={2，4，6}，则 A∪B=

查看试题解析
2. 某学校高一、高二、高三年级的学生人数之比为3：3：4，现用分层抽样的方法从该校高中三个年级的学生中抽取容量为50的样本，则应从高二年级抽取名学生．

查看试题解析
3. 设a，b∈R，a+bi= $\frac{11 - 7 i}{1 - 2 i}$ （i为虚数单位），则a+b的值为．

查看试题解析
4. 图是一个算法流程图，则输出的k的值是．

查看试题解析
5. 函数f（x）= $\sqrt{1 - 2 \log_{6} x}$ 的定义域为．

查看试题解析
6. 现有10个数，它们能构成一个以1为首项，﹣3为公比的等比数列，若从这10个数中随机抽取一个数，则它小于8的概率是．

查看试题解析
7. 如图，在长方体ABCD﹣A₁B₁C₁D₁中，AB=AD=3cm，AA₁=2cm，则四棱锥A﹣BB₁D₁D的体积为 cm³ ．

查看试题解析
8. 在平面直角坐标系xOy中，若双曲线 $\frac{x^{2}}{m} - \frac{y^{2}}{m^{2} + 4} = 1$ 的离心率为 $\sqrt{5}$ ，则m的值为．

查看试题解析
9. 如图，在矩形ABCD中，AB= $\sqrt{2}$ ，BC=2，点E为BC的中点，点F在边CD上，若 $\vec{A B} \cdot \vec{A F}$ = $\sqrt{2}$ ，则 $\vec{A E} \cdot \vec{B F}$ 的值是

查看试题解析
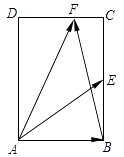10. 设f（x）是定义在R上且周期为2的函数，在区间[﹣1，1]上，f（x）= ${\begin{matrix} a x + 1 ， - 1 \leq x < 0 \\ \frac{b x + 2}{x + 1} ， 0 \leq x \leq 1 \end{matrix}$ 其中a，b∈R．若 $f (\frac{1}{2})$ = $f (\frac{3}{2})$ ，则a+3b的值为．

查看试题解析
11. 设α为锐角，若cos（α+ $\frac{π}{6}$ ）= $\frac{4}{5}$ ，则sin（2α+ $\frac{π}{12}$ ）的值为．

查看试题解析
12. 在平面直角坐标系xOy中，圆C的方程为x²+y²﹣8x+15=0，若直线y=kx﹣2上至少存在一点，使得以该点为圆心，1为半径的圆与圆C有公共点，则k的最大值是．

查看试题解析
13. 已知函数f（x）=x²+ax+b（a，b∈R）的值域为[0，+∞），若关于x的不等式f（x）＜c的解集为（m，m+6），则实数c的值为．

查看试题解析
14. 已知正数a，b，c满足：5c﹣3a≤b≤4c﹣a，clnb≥a+clnc，则 $\frac{b}{a}$ 的取值范围是．

查看试题解析

二、解答题：请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．

15. 在△ABC中，已知 $\vec{A B} \cdot \vec{A C} = 3 \vec{B A} \cdot \vec{B C}$ ．

(1)、求证：tanB=3tanA；

(2)、若cosC= $\frac{\sqrt{5}}{5}$ ，求A的值．

查看试题解析
16. 如图，在直三棱柱ABC﹣A₁B₁C₁中，A₁B₁=A₁C₁ ， D，E分别是棱BC，CC₁上的点（点D 不同于点C），且AD⊥DE，F为B₁C₁的中点．求证：

(1)、平面ADE⊥平面BCC₁B₁；

(2)、直线A₁F∥平面ADE．

查看试题解析
17. 如图，建立平面直角坐标系xOy，x轴在地平面上，y轴垂直于地平面，单位长度为1千米．某炮位于坐标原点．已知炮弹发射后的轨迹在方程y=kx﹣ $\frac{1}{20}$ （1+k²）x²（k＞0）表示的曲线上，其中k与发射方向有关．炮的射程是指炮弹落地点的横坐标．

(1)、求炮的最大射程；

(2)、设在第一象限有一飞行物（忽略其大小），其飞行高度为3.2千米，试问它的横坐标a不超过多少时，炮弹可以击中它？请说明理由．

查看试题解析
18. 若函数y=f（x）在x=x₀处取得极大值或极小值，则称x₀为函数y=f（x）的极值点．已知a，b是实数，1和﹣1是函数f（x）=x³+ax²+bx的两个极值点．

(1)、求a和b的值；

(2)、设函数g（x）的导函数g′（x）=f（x）+2，求g（x）的极值点；

(3)、设h（x）=f（f（x））﹣c，其中c∈[﹣2，2]，求函数y=h（x）的零点个数．

查看试题解析
19. 如图，在平面直角坐标系xOy中，椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ （a＞b＞0）的左、右焦点分别为F₁（﹣c，0），F₂（c，0）．已知（1，e）和（e， $\frac{\sqrt{3}}{2}$ ）都在椭圆上，其中e为椭圆的离心率．

(1)、求椭圆的方程；

(2)、设A，B是椭圆上位于x轴上方的两点，且直线AF₁与直线BF₂平行，AF₂与BF₁交于点P．
（i）若AF₁﹣BF₂= $\frac{\sqrt{6}}{2}$ ，求直线AF₁的斜率；
（ii）求证：PF₁+PF₂是定值．

查看试题解析
20. 已知各项均为正数的两个数列{a_n}和{b_n}满足：a_n+1= $\frac{a_{n} + b_{n}}{\sqrt{a_{n}^{2} + b_{n}^{2}}}$ ，n∈N^* ，

(1)、设b_n+1=1+ $\frac{b_{n}}{a_{n}}$ ，n∈N*，求证：数列{ ${(\frac{b_{n}}{a_{n}})}^{2}$ }是等差数列；

(2)、设b_n+1= $\sqrt{2}$ • $\frac{b_{n}}{a_{n}}$ ，n∈N*，且{a_n}是等比数列，求a₁和b₁的值．

查看试题解析

三、附加题(21选做题：任选2小题作答，22、23必做题）

21.

(1)、
[选修4﹣1：几何证明选讲]
如图，AB是圆O的直径，D，E为圆上位于AB异侧的两点，连接BD并延长至点C，使BD=DC，连接AC，AE，DE．
求证：∠E=∠C．

(2)、[选修4﹣2：矩阵与变换]
已知矩阵A的逆矩阵 $A^{- 1} = [\begin{matrix} - \frac{1}{4} & \frac{3}{4} \\ \frac{1}{2} & - \frac{1}{2} \end{matrix}]$ ，求矩阵A的特征值．

(3)、[选修4﹣4：坐标系与参数方程]
在极坐标中，已知圆C经过点P（ $\sqrt{2}$ ， $\frac{π}{4}$ ），圆心为直线ρsin（θ﹣ $\frac{π}{3}$ ）=﹣ $\frac{\sqrt{3}}{2}$ 与极轴的交点，求圆C的极坐标方程．

(4)、[选修4﹣5：不等式选讲]
已知实数x，y满足：|x+y|＜ $\frac{1}{3}$ ，|2x﹣y|＜ $\frac{1}{6}$ ，求证：|y|＜ $\frac{5}{18}$ ．

查看试题解析
22. 设ξ为随机变量，从棱长为1的正方体的12条棱中任取两条，当两条棱相交时，ξ=0；当两条棱平行时，ξ的值为两条棱之间的距离；当两条棱异面时，ξ=1．

(1)、求概率P（ξ=0）；

(2)、求ξ的分布列，并求其数学期望E（ξ）．

查看试题解析
23. 设集合P_n={1，2，…，n}，n∈N^* ．记f（n）为同时满足下列条件的集合A的个数：
①A⊆P_n；②若x∈A，则2x∉A；③若x∈ $∁_{P_{n}}$ A，则2x∉ $∁_{P_{n}}$ A．

(1)、求f（4）；

(2)、求f（n）的解析式（用n表示）．

查看试题解析