浙江省北斗星盟2022届高三下学期数学5月联考试卷

试卷更新日期：2022-06-17 类型：高考模拟

进入出卷网下载

一、单选题

1. 设全集 $U = R$ ，集合 $A = {x | x \geq 1}$ ， $B = {x | - 1 \leq x \leq 2}$ ，则 $(∁_{U} A) ∩ B =$ （）

A、 ${x | - 1 \leq x < 1}$ B、 ${x | x > 2}$ C、 ${x | x \leq 2}$ D、 ${x | 1 \leq x \leq 2}$

查看试题解析
2. 已知复数 $z = \frac{1 + a i}{2 + i}$ 是纯虚数（其中i是虚数单位），则实数a的值为（）

A、2 B、-2 C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
3. 某几何体的三视图如图所示，则该几何体的体积是（）

A、 $π + 4$ B、 $2 π + 4$ C、 $π + \frac{8}{3}$ D、 $2 π + \frac{8}{3}$

查看试题解析
4. 若 $x$ ， $y$ 满足约束条件 ${\begin{array}{l} x - y + 1 \geq 0 \\ x - 2 y \leq 0 \\ x + 2 y - 2 \leq 0 \end{array}$ ，则 $z = x + y$ 的最大值为（）

A、-3 B、1 C、3 D、 $\frac{3}{2}$

查看试题解析
5. 非直角 $△ A B C$ 中，内角A，B，C所对的边分别为a，b，c，则“ $a > b$ ”是“ $t a n A > t a n B$ ”的（）条件

A、充分不必要 B、必要不充分 C、充分必要 D、既不充分也不必要

查看试题解析
6. 在 $△ A B C$ 中，E，F分别为 $A C ， B C$ 的中点，点D是线段 $A F$ （不含端点）内的任意一点， $\vec{A D} = m \vec{A B} + n \vec{A E}$ ，则（）

A、 $m \in (0 ， 1)$ B、 $n \in (0 ， 2)$ C、 $n = 2 m$ D、 $m + n = 1$

查看试题解析
7. 已知函数 $f (x)$ 的部分图像如图所示，则该函数的解析式可能是（）

A、 $f (x) = x^{2} + l n \frac{2 + c o s x}{2 - c o s x}$ B、 $f (x) = x^{3} l n \frac{2 + c o s x}{2 - c o s x}$ C、 $f (x) = x^{3} + l n \frac{2 + s i n x}{2 - s i n x}$ D、 $f (x) = x^{2} l n \frac{2 + s i n x}{2 - s i n x}$

查看试题解析
8. 如图，在单位正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，点P是线段 $A D_{1}$ 上的动点，给出以下四个命题：
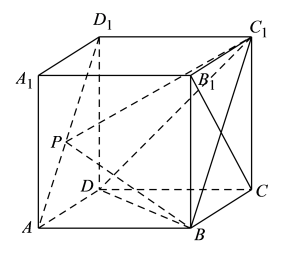
①异面直线 $P C_{1}$ 与直线 $B_{1} C$ 所成角的大小为定值；②二面角 $P - B C_{1} - D$ 的大小为定值；③若Q是对角线 $A C_{1}$ 上一点，则 $P Q + Q C$ 长度的最小值为 $\frac{4}{3}$ ；④若R是线段 $B D$ 上一动点，则直线PR与直线 $A_{1} C$ 不可能平行．
其中真命题有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 已知 $s i n x ， s i n y ， s i n z$ 依次组成严格递增的等差数列，则下列结论错误的是（）

A、 $t a n x ， t a n y ， t a n z$ 依次可组成等差数列 B、 $c o s x ， c o s y ， c o s z$ 依次可组成等差数列 C、 $c o s x ， c o s z ， c o s y$ 依次可组成等差数列 D、 $c o s z ， c o s x ， c o s y$ 依次可组成等差数列

查看试题解析
10. 记 $U = {1 ， 2 ， ⋯ ， 100}$ ．对数列 ${a_{n}} (n \in N^{*})$ 和U的子集T，若 $T = \emptyset$ ，定义 $S_{T} = 0$ ；若 $T = {t_{1} ， t_{2} ， ⋯ ， t_{k}}$ ，定义 $S_{T} = a_{t_{1}} + a_{t_{2}} + ⋯ + a_{t_{k}}$ ．则以下结论正确的是（）

A、若 ${a_{n}} (n \in N^{*})$ 满足 $a_{n} = 2 n - 1 ， T = {1 ， 2 ， 4 ， 8}$ ，则 $S_{T} = 15$ B、若 ${a_{n}} (n \in N^{*})$ 满足 $a_{n} = 2 n - 1$ ，则对任意正整数 $k (1 \leq k \leq 100) ， T \subseteq {1 ， 2 ， ⋯ ， k} ， S_{T} < a_{k}$ C、若 ${a_{n}} (n \in N^{*})$ 满足 $a_{n} = 3^{n - 1}$ ，则对任意正整数 $k (1 \leq k \leq 100) ， T \subseteq {1 ， 2 ， ⋯ ， k} ， S_{T} \geq a_{k + 1}$ D、若 ${a_{n}} (n \in N^{*})$ 满足 $a_{n} = 3^{n - 1}$ ，且 $C \subseteq U ， D \subseteq U ， S_{C} \geq S_{D}$ ，则 $S_{C} + S_{C ∩ D} \geq 2 S_{D}$

查看试题解析

二、填空题

11. 法国数学家蒙日（Monge， $1746 - 1818$ ）发现：椭圆 $Γ ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的两条互相垂直切线的交点 $P$ 的轨迹方程为： $x^{2} + y^{2} = a^{2} + b^{2}$ ，这个圆被称为蒙日圆．若某椭圆 $\frac{x^{2}}{a^{2}} + y^{2} = 1 (a > 1)$ 对应的蒙日圆方程为 $x^{2} + y^{2} = 5$ ，则 $a =$ ．

查看试题解析
12. 已知平面向量 $\vec{a} ， \vec{b}$ 满足 $| \vec{a} | = 4 ， | \vec{b} | \leq 1$ ，且 $| \vec{a} - 3 \vec{b} | \leq \sqrt{13}$ ，则向量 $\vec{a}$ 在向量 $\vec{b}$ 方向上的投影的最小值为．

查看试题解析
13. 已知点F为双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左焦点，A为直线 $l ： y = \frac{b}{a} x$ 在第一象限内的点，过原点O作 $O A$ 的垂线交 $F A$ 于点B，且B恰为线段 $A F$ 的中点，若 $△ A B O$ 的内切圆半径为 $\frac{b - 2 a}{4} (b > 2 a)$ ，则该双曲线的离心率大小为．

查看试题解析
14. ${(\frac{1}{x} - \sqrt{x})}^{n}$ 的展开式中，若只有第6项的二项式系数最大，则 $n =$ ， $x^{2}$ 的系数为．

查看试题解析
15. 在 $△ A B C$ 中， $∠ A C B = 90 °$ ，点D，E分别在线段 $B C ， A B$ 上， $A C = B C = 3 B D = 3$ ， $∠ E D C = 60 °$ °，则 $D E =$ ， $△ B C E$ 的面积等于．

查看试题解析
16. 用数字1，2，3，4，5给3名男生和2名女生随机地编学号，则男生和女生的学号都不相邻的编法有种（用数字作答）；记随机变量 $ξ = X - Y$ ，其中X，Y分别为男生、女生的学号之和，则随机变量 $ξ$ 的数学期望 $E (ξ) =$ ．

查看试题解析
17. 已知函数 $f (x) = {\begin{array}{l} \frac{x}{e^{x}} ， x < a ， \\ - x^{2} + 4 x ， x \geq a ， \end{array}$ 当 $a = 3$ 时，函数 $f (x)$ 有个零点；记函数 $f (x)$ 的最大值为 $g (a)$ ，则 $g (a)$ 的值域为．

查看试题解析

三、解答题

18. 已知函数 $f (x) = 2 s i n (\frac{π}{4} - x) c o s (\frac{π}{4} - x) - c o s (\frac{π}{3} + 2 x)$

(1)、求函数 $f (x)$ 的最小正周期；

(2)、在锐角 $△ A B C$ 中，内角A，B，C所对的边分别为a，b，c，若 $f (\frac{C}{2}) = 1$ ，且 $c^{2} = a b$ ，试判断 $△ A B C$ 的形状．

查看试题解析
19. 如图，已知三棱台 $A B C - A_{1} B_{1} C_{1}$ 中，点 $A_{1}$ 在平面 $A B C$ 内的射影D在 $B C$ 上， $A A_{1} = A B = 4$ ， $∠ A_{1} A C = 30 °$ ， $∠ B A C = 90 °$ ， M，N分别为 $A_{1} C_{1}$ 、 $B C_{1}$ 的中点．

(1)、证明：直线 $M N / /$ 平面 $A B B_{1} A_{1}$ ；

(2)、若 $A_{1} D = \sqrt{3}$ ，求直线 $M N$ 与平面 $A C C_{1} A_{1}$ 所成角的大小．

查看试题解析
20. 在数列 ${a_{n}}$ 中， $a_{1} = 1 ， a_{2} = 2$ ，且对任意的 $n \in N^{*}$ ，都有 $a_{n + 2} = 3 a_{n + 1} - 2 a_{n}$ ．

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、若 $A = {x | x_{1} < x < x_{2} 或 x_{3} < x < x_{4}}$ ，定义集合A的长度为 $| x_{4} - x_{3} | + | x_{2} - x_{1} |$ ．已知数列 ${b_{n}}$ 的通项公式为 $b_{n} = \frac{a_{n} x}{(a_{1} x + 1) (a_{2} x + 1) ⋯ (a_{n} x + 1)} (n \in N^{*})$ ，若关于x不等式 $b_{1} + b_{2} + ⋯ + b_{2022} > 1$ 的解集A，求集合A的长度．

查看试题解析
21. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左、右焦点为 $F_{1} ， F_{2}$ ，焦距为2，点P是椭圆C上一点满足 $P F_{2} ⊥ x$ 轴， $| P F_{1} | = 3 | P F_{2} |$ ．

(1)、求椭圆C的方程；

(2)、过 $F_{2}$ 的直线交椭圆C于A，B（异于点P）两点，直线 $O A ， O B$ 分别交直线 $P F_{2}$ 于M，N，记 $S_{△ A M F_{2}} = S_{1} ， S_{△ B N F_{2}} = S_{2}$ ，求 $\frac{1}{S_{1}} + \frac{1}{S_{2}}$ 的最小值．

查看试题解析
22. 函数 $f (x) = l n x - \frac{x^{2}}{a} + 1 (a \in R ， a \neq 0)$ ．

(1)、讨论函数 $y = f (x)$ 的单调性；

(2)、若函数 $y = f (x)$ 有两个零点 $x_{1} ， x_{2}$ ，且 $x_{1} < x_{2}$ ，
①证明： $x_{1} + x_{2} > \frac{2}{\sqrt{e}}$ ；
②证明： $\frac{a}{2} - \frac{1}{\sqrt{e}} < x_{2}^{2} - x_{1} < a^{2} + a - 1$ ．（注： $e = 2.71828 \cdot \cdot \cdot$ 为自然对数的底数）

查看试题解析