浙江省2022届高三下学期数学高考模拟预测试卷

试卷更新日期：2022-06-17 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知集合 $M = {- 1 ， 0 ， 1}$ ，则集合 $M$ 的子集的个数共有（）

A、5 B、6 C、7 D、8

查看试题解析
2. 已知复数 $\bar{z} = 1 + 3 i$ ，则 $\frac{1}{z} =$ （）

A、 $\frac{1}{10} + \frac{3}{10} i$ B、 $\frac{1}{10} - \frac{3}{10} i$ C、 $- \frac{1}{10} + \frac{3}{10} i$ D、 $- \frac{1}{10} - \frac{3}{10} i$

查看试题解析
3. “ $m > 0$ 且 $n > 0$ ”是“方程 $m x^{2} + n y^{2} = 1$ 表示椭圆”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分又不必要条件

查看试题解析
4. 若 $x$ ， $y$ 满足约束条件 ${\begin{array}{l} x - y + 1 \geq 0 \\ x - 2 y \leq 0 \\ x + 2 y - 2 \leq 0 \end{array}$ ，则 $z = x + y$ 的最大值为（）

A、-3 B、1 C、3 D、 $\frac{3}{2}$

查看试题解析
5. 某几何体的三视图如图所示，则该几何体的体积是（）

A、 $π + 4$ B、 $2 π + 4$ C、 $π + \frac{8}{3}$ D、 $2 π + \frac{8}{3}$

查看试题解析
6. 智能主动降噪耳机工作的原理是通过耳机两端的噪声采集器采集周围的噪音，然后通过听感主动降噪芯片生成相等的反向波抵消噪音（如图）．已知某机器工作时噪音的声波曲线 $y = A s i n (ω x + φ)$ （其中 $A > 0 ， ω > 0$ ）的振幅为2，周期为 $\frac{π}{2}$ ，初相为 $\frac{π}{3}$ ，则通过听感主动降噪芯片生成相等的反向波曲线为（）

A、 $y = 2 s i n (4 x + \frac{π}{3})$ B、 $y = 2 c o s (4 x + \frac{π}{3})$ C、 $y = 2 s i n (4 x + \frac{4 π}{3})$ D、 $y = 2 c o s (4 x + \frac{4 π}{3})$

查看试题解析
7. 如图，平面 $A B C D ⊥$ 平面 $A B E F$ ，四边形 $A B C D$ 是正方形，四边形 $A B E F$ 是矩形，且 $A B = 4$ ， $A F = 1$ ，若 $G$ 是线段 $E F$ 上的动点，则三棱锥 $C - A B G$ 的外接球表面积的最小值是（）

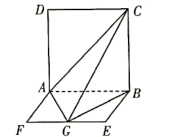A、16π B、20π C、32π D、36π

查看试题解析
8. 已知函数 $f (x)$ 的部分图像如图所示，则该函数的解析式可能是（）

A、 $f (x) = x^{2} + l n \frac{2 + c o s x}{2 - c o s x}$ B、 $f (x) = x^{3} l n \frac{2 + c o s x}{2 - c o s x}$ C、 $f (x) = x^{3} + l n \frac{2 + s i n x}{2 - s i n x}$ D、 $f (x) = x^{2} l n \frac{2 + s i n x}{2 - s i n x}$

查看试题解析
9. 已知双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的离心率为2， $F_{1} ， F_{2}$ 分别是双曲线的左、右焦点，点 $M (- a ， 0)$ ， $N (0 ， b)$ ，点 $P$ 为线段 $M N$ 上的动点，当 $\vec{P F_{1}} \cdot \vec{P F_{2}}$ 取得最大值和最小值时， $△ P F_{1} F_{2}$ 的面积分别为 $S_{1} ， S_{2}$ ，则 $\frac{S_{1}}{S_{2}} =$ （）

A、4 B、8 C、 $2 \sqrt{3}$ D、 $4 \sqrt{3}$

查看试题解析
10. 记 $U = {1 ， 2 ， ⋯ ， 100}$ ．对数列 ${a_{n}} (n \in N^{*})$ 和U的子集T，若 $T = \emptyset$ ，定义 $S_{T} = 0$ ；若 $T = {t_{1} ， t_{2} ， ⋯ ， t_{k}}$ ，定义 $S_{T} = a_{t_{1}} + a_{t_{2}} + ⋯ + a_{t_{k}}$ ．则以下结论正确的是（）

A、若 ${a_{n}} (n \in N^{*})$ 满足 $a_{n} = 2 n - 1 ， T = {1 ， 2 ， 4 ， 8}$ ，则 $S_{T} = 15$ B、若 ${a_{n}} (n \in N^{*})$ 满足 $a_{n} = 2 n - 1$ ，则对任意正整数 $k (1 \leq k \leq 100) ， T \subseteq {1 ， 2 ， ⋯ ， k} ， S_{T} < a_{k}$ C、若 ${a_{n}} (n \in N^{*})$ 满足 $a_{n} = 3^{n - 1}$ ，则对任意正整数 $k (1 \leq k \leq 100) ， T \subseteq {1 ， 2 ， ⋯ ， k} ， S_{T} \geq a_{k + 1}$ D、若 ${a_{n}} (n \in N^{*})$ 满足 $a_{n} = 3^{n - 1}$ ，且 $C \subseteq U ， D \subseteq U ， S_{C} \geq S_{D}$ ，则 $S_{C} + S_{C ∩ D} \geq 2 S_{D}$

查看试题解析

二、填空题

11. 在等差数列 ${a_{n}}$ 中， $a_{1} = - 9 ， a_{5} = - 1$ ，记 $T_{n} = a_{1} a_{2} ⋯ a_{n} (n = 1 ， 2 ， ⋯)$ ，则数列 ${T_{n}}$ 最大项的值为.

查看试题解析
12. 若 $| \vec{a} | = 1$ ， $| \vec{b} | = 2$ ， $\vec{c} = \vec{a} + \vec{b}$ 且 $\vec{c} ⊥ \vec{a}$ ，则向量 $\vec{a}$ 与 $\vec{b}$ 的夹角为．

查看试题解析
13. 2021年7月25日召开的第44届世界遗产大会上，“泉州：宋元中国的世界海洋商贸中心”获准列入世界文化遗产名录，至此泉州20年的申遗终于圆梦.申遗的遗产点包括九日山祈风石刻､开元寺､洛阳桥等22处代表性古遗迹，这些古遗迹可分为文化纪念地史迹等五类.这五类古遗迹充分展现了10-14世纪泉州完备的海洋贸易制度体系､发达的经济水平及多元包容的文化态度.某校中学生准备到各类古遗迹打卡，已知该同学打卡第一类､第二类的概率都是 $\frac{2}{3}$ ，打卡第三类､第四类和第五类的概率都是 $\frac{1}{2}$ ，且是否打卡这五类古遗迹相互独立.用随机变量 $X$ 表示该同学打卡的类别数，则 $P (X = 4) =$ .

查看试题解析
14. 已知 $\vec{e_{1}} ， \vec{e_{2}}$ 是空间单位向量， $\vec{e_{1}} \cdot \vec{e_{2}} = \frac{1}{2}$ 若空间向量 $b$ 满足 $\vec{b} \cdot \vec{e_{1}} = 2$ ， $\vec{b} \cdot \vec{e_{2}} = \frac{5}{2}$ ，且对于任意x，y∈R， $| \vec{b} - (x \vec{e_{1}} + y \vec{e_{2}}) | ⩾ | \vec{b} - (x_{0} \vec{e_{1}} + y_{0} \vec{e_{2}}) | = \sqrt{2} (x_{0} ， y_{0} \in R)$ ，则 $x_{0} + y_{0} + | \vec{b} |$ = ．

查看试题解析
15. ${(\frac{1}{x} - \sqrt{x})}^{n}$ 的展开式中，若只有第6项的二项式系数最大，则 $n =$ ， $x^{2}$ 的系数为．

查看试题解析
16. 在 $△ A B C$ 中， $∠ A C B = 90 °$ ，点D，E分别在线段 $B C ， A B$ 上， $A C = B C = 3 B D = 3$ ， $∠ E D C = 60 °$ °，则 $D E =$ ， $△ B C E$ 的面积等于．

查看试题解析
17. 在棱长为 $\sqrt{3}$ 的正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，P为侧面 $B C C_{1} B_{1}$ 内的动点，且直线 $A_{1} P$ 与 $A B$ 的夹角为30°，则点P的轨迹长为；若点 $A_{1}$ 与动点P均在球O表面上，球O的表面积为．

查看试题解析

三、解答题

18. 记 $△ A B C$ 的内角 $A$ ， $B$ ， $C$ 所对的边分别为 $a$ ， $b$ ， $c$ ，已知 $b s i n C = s i n C + \sqrt{3} c o s C$ ， $A = \frac{π}{3}$ ．

(1)、求 $c$ ；

(2)、在下列三个条件中选择一个作为补充条件，判断该三角形是否存在？若存在，求出三角形的面积；若不存在，说明理由．
① $B C$ 边上的中线长为 $\frac{\sqrt{2}}{2}$ ， ②AB边上的中线长为 $\sqrt{7}$ ， ③三角形的周长为 $6$ ．注：如果选择多个条件分别解答，按第一个解答计分．

查看试题解析
19. 如图，在四棱锥 $S - A B C D$ 中，底面 $A B C D$ 是矩形，平面 $S B C ⊥$ 平面 $A B C D$ ， $S B = S C$ ， M是 $B C$ 的中点，连接 $A M$ ， $A B = 1$ ， $B C = 2$ ．

(1)、求证： $A M ⊥ S D$ ；

(2)、若 $S D = 2$ ，求直线 $A D$ 与平面 $S C D$ 所成角的余弦值．

查看试题解析
20. 已知各项均为正数的数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n} ， a_{1} = 1 ， a_{n} = \sqrt{S_{n}} + \sqrt{S_{n - 1}} (n \in N^{*} ， n \geq 2)$ .

(1)、求证；数列 ${\sqrt{S_{n}}}$ 是等差数列，并求 ${a_{n}}$ 的通项公式；

(2)、若 $[x]$ 表示不超过 $x$ 的最大整数，如 $[- 1 ， 2] = - 2 ， [2 ， 1] = 2$ ，求 $[\frac{1}{a_{1}^{2}} + \frac{1}{a_{2}^{2}} + ⋯ + \frac{1}{a_{n}^{2}}]$ 的值.

查看试题解析
21. 如图，已知F是抛物线 $y^{2} = 2 p x (p > 0)$ 的焦点，M是抛物线的准线与x轴的交点，且 $| M F | = 2$ ，

(1)、求抛物线的方程；

(2)、设过点F的直线交抛物线与A､B两点，斜率为2的直线l与直线 $M A ， M B ， A B$ ，x轴依次交于点P ， Q ， R ， N ，且 ${| R N |}^{2} = | P N | \cdot | Q N |$ ，求直线l在x轴上截距的范围.

查看试题解析
22. 已知函数 $f (x) = a e^{2 x} + (a - 2) e^{x} - x$ .

(1)、讨论 $f (x)$ 的单调性；

(2)、若 $f (x)$ 有两个零点，求 $a$ 的取值范围；

(3)、求证： $e^{2 x} - x > \frac{e}{6} (x^{3} + 3 x + 2)$ .

查看试题解析