江苏省南通市如皋市2022届高三下学期数学5月适应性考试试卷（三）

试卷更新日期：2022-06-17 类型：高考模拟

进入出卷网下载

一、单选题

1. 设集合 $A = {(x ， y) | 2 x - y = 0}$ ， $B = {y | y = x^{2} - 2 x + 3}$ ，则 $A ∩ B =$ （）

A、 ${1 ， 3}$ B、 ${(1 ， 2) ， (3 ， 6)}$ C、 ${y | y \geq 2}$ D、 $\emptyset$

查看试题解析
2. 在复平面内，O为坐标原点，复数4i对应的向量为 $\vec{O Z}$ ，将 $\vec{O Z}$ 绕点O按逆时针方向旋转60°后，再将模变为原来的 $\sqrt{3}$ 倍，得到向量 $\vec{O Z_{1}}$ ，则 $\vec{O Z_{1}}$ 对应的复数的实部是（）

A、6 B、－6 C、 $2 \sqrt{3}$ D、 $- 2 \sqrt{3}$

查看试题解析
3. 若m＞n＞1，则下列各式一定成立的是（）

A、 $2^{- m} > 2^{- n}$ B、 $(m - 1)^{n} > 1$ C、log₂（m－1）＞log₂（n－1） D、 $l o g_{n} (m - 1) > 0$

查看试题解析
4. 某市卫健委用模型 $y = l n (k x + b) + 1$ 的回归方程分析2022年4月份感染新冠肺炎病毒的人数，令 $z = e^{y}$ 后得到的线性回归方程为 $z = 3 x + e$ ，则 $b =$ （）

A、1 B、 $e - 1$ C、 $e$ D、 $3 e$

查看试题解析
5. 甲、乙、丙、丁共4名同学进行国庆演讲比赛决赛，决出第一名到第四名．甲、乙两人中一人获得第一名，另一人不是第四名，则4人名次所有不同结果的总数为（）

A、4 B、6 C、8 D、10

查看试题解析
6. 在平面直角坐标系xOy中，点F为抛物线C：y²=4x的焦点，以F为圆心且与抛物线C的准线相切的圆F交抛物线C于A，B，则|AB|=（）

A、2 B、4 C、 $2 \sqrt{3}$ D、 $4 \sqrt{3}$

查看试题解析
7. 函数 $f (x) = x^{3} - a x + a - 1$ 有两个零点的一个充分不必要条件是（）

A、a=3 B、a=2 C、a=1 D、a=0

查看试题解析
8. 小强计划制作一个三角形，使得它的三条边中线的长度分别为1， $\sqrt{7}$ ， $\sqrt{7}$ ，则（）

A、能制作一个锐角三角形 B、能制作一个直角三角形 C、能制作一个钝角三角形 D、不能制作这样的三角形

查看试题解析

二、多选题

9. 已知函数 $f (x) = s i n (2 x + \frac{π}{3})$ ，先将 $y = f (x)$ 的图象上所有点的纵坐标不变，横坐标变为原来的4倍，再将图象向右平移 $\frac{π}{6}$ 个单位长度，得到函数 $y = g (x)$ 的图象，则（）

A、 $g (x) = s i n (\frac{1}{2} x + \frac{π}{6})$ B、 $g (x)$ 的图象关于 $x = - \frac{7 π}{2}$ 对称 C、 $g (x)$ 的最小正周期为 $4 π$ D、 $g (x)$ 在 $(- 3 π ， - \frac{3}{2} π)$ 上单调递减

查看试题解析
10. 函数 $f (x) = \frac{a x l n x}{e^{x}}$ 的大致图象可能为（）

A、 B、 C、 D、

查看试题解析
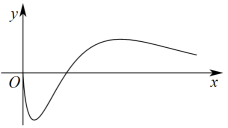11. 在平面直角坐标系xOy中，已知F₁ ， F₂分别是椭圆 $C ： \frac{x^{2}}{4} + \frac{y^{2}}{2} = 1$ 的左，右焦点，点A，B是椭圆C上异于长轴端点的两点，且满足 ${\vec{A F}}_{1} = λ \vec{F_{1} B}$ ，则（）

A、△ABF₂的周长为定值 B、AB的长度最小值为1 C、若AB⊥AF₂ ，则λ=3 D、λ的取值范围是[1，5]

查看试题解析
12. 某工艺品如图I所示，该工艺品由正四棱锥嵌入正四棱柱（正四棱柱的侧棱平行于正四棱锥的底面）得到，如图II，已知正四棱锥V－EFGH的底面边长为 $3 \sqrt{2}$ ，侧棱长为5，正四棱柱ABCD－A₁B₁C₁D₁的底边边长为a，且BB₁∩VF=M，DD₁∩VH=N，AA₁∩VE=P，AA₁∩VG=Q，CC₁∩VE=R，CC₁∩VG=S，则（）

A、当M为棱VF中点时， $a = \frac{3 \sqrt{2}}{2}$ B、PM＜MR C、存在实数a，使得PM⊥MR D、线段MN长度的最大值 $\frac{24}{7}$

查看试题解析

三、填空题

13. 某学习兴趣小组的某学生的10次测试成绩如下：130，135，126，123，145，146，150，131，143，144，则该学生的10次测验成绩的45百分位数是．

查看试题解析
14. $(x - 1) (x + y)^{4}$ 的展开式中 $x^{3} y^{2}$ 的系数为．

查看试题解析
15. 小强对重力加速度做n次实验，若以每次实验结果的平均值作为重力加速度的估值．已知估值的误差 $Δ_{n} ∼ N (0 ， \frac{9}{n^{2}})$ ，为使误差 $Δ_{n}$ 在 $(- 0.5 ， 0.5)$ 内的概率不小于0.6827，至少要实验次．（参考数据：若 $X ∼ N (μ ， σ^{2})$ ，则 $P (μ － σ \leq X \leq μ ＋ σ) = 0.6827$ ）．

查看试题解析
16. 雪花曲线是瑞典数学家科赫在1904年研究的一种分形曲线．如图是“雪花曲线”的一种形成过程：从图①的正三角形开始，把每条边分成三等份，然后以各边的中间一段为底边分别向外作正三角形，再去掉底边得到图②，重复进行这一过程可依次得到图③、图④等一系列“雪花曲线”．
① ② ③ ④
若第①个图中的三角形的边长为1，则第②个图形的面积为；第n个图中“雪花曲线”的周长Cn为．

查看试题解析

四、解答题

17. 已知圆的内接四边形ABCD中， $A B = A D = 2 \sqrt{2}$ ， BC=2， $C D = 2 \sqrt{3}$ ．

(1)、求四边形ABCD的面积；

(2)、设边AB，CD的中点分别为E，F，求 $\vec{F E} \cdot (\vec{A B} + \vec{C D})$ 的值．

查看试题解析
18. 已知等差数列{an}满足a₅=16，a₇=22，正项等比数列{bn}的前n项和为Sn，满足S₆=5S₄－4S₂ ，且b₂=a₁ ．

(1)、求{an}和{bn}的通项公式；

(2)、是否存在n使得 $\frac{a_{n}}{b_{n}} \in Z$ ，若存在，求出所有n的值；若不存在，请说明理由．

查看试题解析
19. 如图，四边形ABCD是一个半圆柱的轴截面，E，F分别是弧DC，AB上的一点，EF $/ /$ AD，点G，H均为所在线段的中点，且AB=AD=6，∠FBA=60°．

(1)、证明：DG $/ /$ 平面CFH；

(2)、求二面角C－HF－E的大小．

查看试题解析
20. 篮球诞生美国马萨诸塞州的春田学院.1891年，春田学院的体育教师加拿大人詹姆斯奈史密斯博士（James Naismith）为了对付冬季寒冷的气温，让学生们能够在室内有限的空间里继续进行有趣的传球训练．现有甲、乙、丙3名同学在某次传球的训练中，球从甲开始，等可能地随机传向另外2人中的1人，接球者接到球后再等可能地随机传向另外2人中的1人，如此不停地传下去，假设传出的球都能接住．记第n次传球之前球在甲手里的概率为pn，第n次传球之前球在乙手里的概率为qn，显然p₁=1，q₁=0．

(1)、求p₃＋2q₃的值；

(2)、比较p₈ ， q₈的大小．

查看试题解析
21. 已知双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的焦距为 $2 \sqrt{2}$ ，设该双曲线的左，右顶点分别为A，B，以点A，B和虚轴端点为顶点的四边形的面积为S．

(1)、当S最大时，求双曲线的标准方程；

(2)、在（1）的条件下，过点A的直线l₁与右支交于点C，过点B的直线l₂与左支交于点D，设直线 $l_{1} ， l_{2}$ 的斜率分别为 $k_{1} ， k_{2}$ ，且 $k_{1} = 3 k_{2}$ ，设 $△ A D C$ ， $△ B C D$ 的面积分别为 $S_{1}$ ， $S_{2}$ ， $\frac{S_{1}}{S_{2}}$ 的值．

查看试题解析
22. 已知函数 $f (x) = {\begin{array}{l} \frac{1}{x} (1 + l n x) ， \frac{1}{e} \leq x \leq 1 \\ x (1 - l n x) ， x > 1 \end{array}$ ．

(1)、求f（x）的最大值；

(2)、设实数m，n满足－1≤m＜0＜n≤1，且 $e^{m + n} = \frac{1 + m}{1 - n}$ ，求证： $2 < e^{m} + e^{n} \leq e + \frac{1}{e}$ ．

查看试题解析