浙江省宁波市2022年6月中考模拟考试数学试卷
试卷更新日期:2022-06-16 类型:中考模拟
一、选择题(每小题4分,共40分)
-
1. 2022 的相反数是( )A、2022 B、-2022 C、 D、2. 已知2x=3y,则下列比例式成立的是( )A、 B、 C、 D、3. 下列等式一定成立的是( )A、 B、 C、 D、4. 抛物线 y=x2﹣6x+4 的顶点坐标是( )A、(3,5) B、(-3,5) C、(3,-5) D、(-3,-5)5. 在四张完全相同的卡片上,分别画有圆,等腰三角形,直角三角形,菱形,现从中随机抽取一张,卡片上的图形恰好是中心对称图形的概率是( )A、 B、 C、 D、16.
如图,AB∥CD,AE平分∠CAB交CD于点E,若∠C=50°,则∠AED=( )
 A、65° B、115° C、125° D、130°7. 已知圆锥的底面半径为 3cm ,高线长为4cm ,则这个圆锥的侧面积为( )A、 B、 C、 D、8. 如图,将△ABC放在每个小正方形的边长为1的网格中,点A,B,C均在格点上,则tanA的值是( )
A、65° B、115° C、125° D、130°7. 已知圆锥的底面半径为 3cm ,高线长为4cm ,则这个圆锥的侧面积为( )A、 B、 C、 D、8. 如图,将△ABC放在每个小正方形的边长为1的网格中,点A,B,C均在格点上,则tanA的值是( )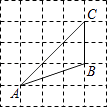 A、 B、 C、2 D、9. 已知 的直径 , 是 的弦, ,垂足为 ,且 ,则 的长为( )A、 B、 C、 或 D、 或10. 如图是由7个等边三角形拼成的图形,若要求出阴影部分的面积,则只需要知道( )
A、 B、 C、2 D、9. 已知 的直径 , 是 的弦, ,垂足为 ,且 ,则 的长为( )A、 B、 C、 或 D、 或10. 如图是由7个等边三角形拼成的图形,若要求出阴影部分的面积,则只需要知道( ) A、⑤和③的面积差 B、③和②的面积差 C、④和②的面积差 D、⑤和②的面积差
A、⑤和③的面积差 B、③和②的面积差 C、④和②的面积差 D、⑤和②的面积差二、填空题(每小题 5 分,共 30 分)
-
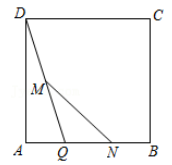
11. 因式分解:3a2-3= .12. 中国的陆地面积约为 ,把9600000用科学记数法表示为 .13. 关于 的一元二次方程 有两个实数根,则 的取值范围是.14. 如图,在正方形 ABCD 中,AB=6,点 Q 是 AB 边上的一个动点(点 Q 不与点 B 重合),点 M,N 分别是 DQ,BQ 的中点,则线段 MN= .
 15. 高尔夫球运动是一项具有特殊魅力的运动,运动员会利用不同的高尔夫球杆将高尔夫球打进球洞,从而使其在优美的自然环境中锻炼身体,并陶冶情操. 如图,某运动员将一只高尔夫球沿某方向击出时,小球的飞行路线是一条抛物线. 如果不考虑空气阻力等因素,小球的飞行高度 (单位:米)与飞行时间 (单位:秒)之间满足函数关系 .则小球从飞出到落地瞬间所需的时间为秒.
15. 高尔夫球运动是一项具有特殊魅力的运动,运动员会利用不同的高尔夫球杆将高尔夫球打进球洞,从而使其在优美的自然环境中锻炼身体,并陶冶情操. 如图,某运动员将一只高尔夫球沿某方向击出时,小球的飞行路线是一条抛物线. 如果不考虑空气阻力等因素,小球的飞行高度 (单位:米)与飞行时间 (单位:秒)之间满足函数关系 .则小球从飞出到落地瞬间所需的时间为秒. 16. 如图,在矩形 ABCD中,点E在边AD上,BE⊥AC 于点F,若AD=2,AB=CF,则sin∠ABE 的值为 .
16. 如图,在矩形 ABCD中,点E在边AD上,BE⊥AC 于点F,若AD=2,AB=CF,则sin∠ABE 的值为 .
三、解答题(第 17-19 题各 8 分,第 20-22 题各 10 分,第 23 题 12 分,第 24 题 14 分,共 80 分)
-
17.(1)、先化简,再求值: , 其中 .(2)、解方程:18. 教育行政部门规定学生每天参加户外活动的平均时间不少于1小时,为了解学生参加户外活动的情况,对部分中学生参加户外活动的时间进行抽样调查,并将调查结果绘制成如下两幅不完整的统计图,请根据图中信息解答下列问题:
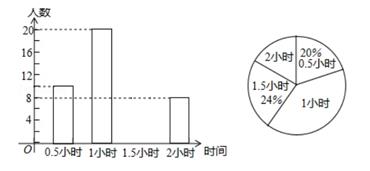 (1)、本次调查中共调查了多少名学生?(2)、将频数分布直方图补充完整(3)、我市九年级学生大约有50000人,请你计算参加户外活动不少于1.5小时的人数.19. 如图,△ACB 和△ECD 都是等腰直角三角形,∠ACB=∠ECD=90°.A,C,D 三点在同一直线上,连结 BD,AE,并延长 AE 交 BD 于 F.
(1)、本次调查中共调查了多少名学生?(2)、将频数分布直方图补充完整(3)、我市九年级学生大约有50000人,请你计算参加户外活动不少于1.5小时的人数.19. 如图,△ACB 和△ECD 都是等腰直角三角形,∠ACB=∠ECD=90°.A,C,D 三点在同一直线上,连结 BD,AE,并延长 AE 交 BD 于 F. (1)、求证:△ACE≌△BCD.(2)、直线 AE 与 BD 互相垂直吗?请证明你的结论.20. 如图,已知 A(-4,n),B(2,-4)是一次函数 y=kx+b 的图象和反比例函数 的图象的两个交点.
(1)、求证:△ACE≌△BCD.(2)、直线 AE 与 BD 互相垂直吗?请证明你的结论.20. 如图,已知 A(-4,n),B(2,-4)是一次函数 y=kx+b 的图象和反比例函数 的图象的两个交点. (1)、求反比例函数和一次函数的解析式;(2)、求△ AOB 的面积;(3)、请直接写出不等式 的解集.21. 如图,已知 内接于 , 是圆外一点, 为 的切线,且 ,连接 ,线段 与线段 相交于点 .
(1)、求反比例函数和一次函数的解析式;(2)、求△ AOB 的面积;(3)、请直接写出不等式 的解集.21. 如图,已知 内接于 , 是圆外一点, 为 的切线,且 ,连接 ,线段 与线段 相交于点 .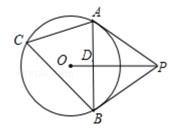 (1)、求证: 为 的切线;(2)、若 , 的半径为5,求线段 的长.22. 新冠肺炎期间,某超市将购进一批口罩进行销售,已知购进4盒甲口罩和6盒乙口罩需260元,购进5盒甲口罩和4盒乙口罩需 220元.两种口罩以相同的售价销售,甲口罩的销量 y1(盒)与售价 x(元)之间的关系为 y1=400﹣8x;当售价为 40 元时,乙口罩可销售 100 盒,售价每提高1元,少销售5盒.(1)、求甲、乙两种口罩每盒的进价分别为多少元?(2)、当乙口罩的售价为多少元时,乙口罩的销售总利润最大?此时两种口罩的销售利润总和为多少?(3)、已知甲的销售量不低于乙口罩的销售量的 ,若使两种口罩的利润总和最高,此时的定价应为多少?23. 定义:若四边形中某个顶点与其它三个顶点的距离相等,则这个四边形
(1)、求证: 为 的切线;(2)、若 , 的半径为5,求线段 的长.22. 新冠肺炎期间,某超市将购进一批口罩进行销售,已知购进4盒甲口罩和6盒乙口罩需260元,购进5盒甲口罩和4盒乙口罩需 220元.两种口罩以相同的售价销售,甲口罩的销量 y1(盒)与售价 x(元)之间的关系为 y1=400﹣8x;当售价为 40 元时,乙口罩可销售 100 盒,售价每提高1元,少销售5盒.(1)、求甲、乙两种口罩每盒的进价分别为多少元?(2)、当乙口罩的售价为多少元时,乙口罩的销售总利润最大?此时两种口罩的销售利润总和为多少?(3)、已知甲的销售量不低于乙口罩的销售量的 ,若使两种口罩的利润总和最高,此时的定价应为多少?23. 定义:若四边形中某个顶点与其它三个顶点的距离相等,则这个四边形叫做等距四边形,这个顶点叫做这个四边形的等距点.
(1)、判断:一个内角为 120°的菱形等距四边形.(填“是”或“不是”)(2)、如图,在 5×5 的网格图中有 A、B 两点,请在答题卷给出的两个网格图上各找出 C、D两个格点,使得以 A、B、C、D 为顶点的四边形为互不全等的“等距四边形”,画出相应的“等距四边形”,并写出该等距四边形的端点均为非等距点的对角线长.
(3)、如图,已知△ ABE 与△ CDE 都是等腰直角三角形,∠AEB=∠DEC=90°,连结 AD,AC ,BC,若四边形 ABCD 是以 A 为等距点的等距四边形,求∠BCD 的度数. 24. 如图,一条抛物线经过原点和点 , 、 是该抛物线上的两点, 轴,点 坐标为 ,点 在线段 上,点 在线段 上,且满足 .
24. 如图,一条抛物线经过原点和点 , 、 是该抛物线上的两点, 轴,点 坐标为 ,点 在线段 上,点 在线段 上,且满足 .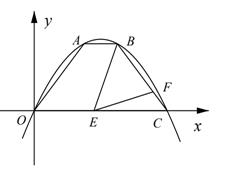 (1)、求抛物线的解析式;(2)、若四边形 的面积为14,求 ;(3)、是否存在点 ,使得 为等腰三角形?若存在,求点 的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、若四边形 的面积为14,求 ;(3)、是否存在点 ,使得 为等腰三角形?若存在,求点 的坐标;若不存在,请说明理由.