浙江省宁波市余姚市2021-2022学年七年级下学期阳明杯学科竞赛（二试）数学试卷

试卷更新日期：2022-06-16 类型：竞赛测试

进入出卷网下载

一、选择题（共10小题，每小题3分，共30分）

1. 如图，能判定直线a∥b的条件是（）

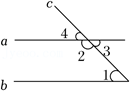A、∠1＝∠2 B、∠3＝∠4 C、∠1+∠3＝180° D、∠1＝∠4

查看试题解析
2. 下列方程中，是二元一次方程的是（）

A、xy＝1 B、 $x - \frac{1}{y} = 3$ C、x＝y D、x+y﹣z＝0

查看试题解析
3. 用科学记数法记录一个较小的数0.00000503，正确的结果应是（）

A、5.03×10^﹣⁶ B、5.03×10^﹣⁷ C、5.03×10^﹣⁸ D、5.03×10^﹣⁹

查看试题解析
4. 为全面掌握小区居民新冠疫苗接种情况，社区工作人员设计了以下几种调查方案：
方案一：调查该小区每栋居民楼的10户家庭成员的疫苗接种情况；
方案二：随机调查该小区100位居民的疫苗接种情况；
方案三：对本小区所有居民的疫苗接种情况逐一调查统计．
在上述方案中，能较好且准确地得到该小区居民疫苗接种情况的是（）

A、方案一 B、方案二 C、方案三 D、以上都不行

查看试题解析
5. 一个多项式的平方是x²+（m﹣2）x+36，则m＝（）

A、﹣10或14 B、﹣14或14 C、12 D、6

查看试题解析
6. 分解因式ab²﹣a，下列结果正确的是（）

A、ab²﹣a＝a（b²﹣1） B、ab²﹣a＝a（b﹣1）² C、ab²﹣a＝a（b+1）（b﹣1） D、ab²﹣a＝a（b+1）²

查看试题解析
7. 要使分式 $\frac{3}{m - 4}$ 有意义，m应满足的条件是（）

A、m＜4 B、m＝4 C、m≠4 D、m＞4

查看试题解析
8. 某施工队整修一条480m的道路．开工后，每天比原计划多整修20m，结果提前4天完成任务．设原计划每天整修xm，根据题意所列方程正确的是（）

A、 $\frac{480}{x + 20} - \frac{480}{x} =$ 4 B、 $\frac{480}{x} - \frac{480}{x - 4} =$ 20 C、 $\frac{480}{x} - \frac{480}{x + 20} =$ 4 D、 $\frac{480}{x - 4} - \frac{480}{x} =$ 20

查看试题解析
9. 已知关于x，y的方程组 ${\begin{array}{l} x + 3 y = 4 - a \\ x - y = 3 a \end{array}$ ，下列结论中正确的有几个（）
①当这个方程组的解x，y的值互为相反数时，a＝﹣2；②当a＝1时，方程组的解也是方程x+y＝4+2a的解；③无论a取什么实数，x+2y的值始终不变；④若用x表示y，则y $= - \frac{x}{2} + \frac{3}{2}$ ；

A、1 B、2 C、3 D、4

查看试题解析
10. 对任意一个两位数n，如果n满足个位与十位上的数字互不相同，且都不为零，那么称这个数为“相异数”，将一个“相异数”的十位上的数字与个位上的数字互换位置后，得到一个新两位数：把所得的新两位数与原两位数的和与11的商记为F（n）．例如n＝23．互换十位与个位上的数字得到32，所得的新两位数与原两位数的和为23+32＝55，55÷11＝5，所以F（23）＝5．若s，t都是“相异数”，其中s＝10x+3，t＝50+y（1≤x≤9，1≤y≤9．x，y都是正整数），当F（s）+F（t）＝15时，则 $\frac{F (s)}{F (t)}$ 的最大值为（）

A、2 B、 $\frac{3}{2}$ C、 $\frac{11}{4}$ D、4

查看试题解析

二、填空题（共6小题，每小题4分，共24分）

11. 已知方程2x+y﹣3＝0，用含x的代数式表示y为：y＝．

查看试题解析
12. 已知a^m＝2，aⁿ＝3，则a^m+n的值为 .

查看试题解析
13. 已知a+b＝5，ab＝﹣3，则﹣2a²b﹣2ab²＝．

查看试题解析
14. 一们同学在解关于x的分式方程 $\frac{a}{x - 3} - \frac{1}{3 - x} = 2$ 的过程中产生了增根，则可以推断a的值为．

查看试题解析
15. 有一条长度为359mm的铜管料，把它锯成长度分别为59mm和39mm两种不同规格的小铜管（要求没有余料），每锯一次损耗1mm的铜管料，为了使铜管料的损耗最少，应分别锯成59mm的小铜管段，39mm的小铜管段．

查看试题解析
16. 响应国家号召，某区推进新型农村建设，强村富民．村民小红家准备将一块良田分成A、B、C三个区域来种植三种畅销型农作物．爸爸计划好三个区域的占地面积后，小红主动承担起实地划分的任务．划分完毕后，爸爸发现粗心的小红将A区20%的面积划分给了B区，而原B区50%的面积错划分给了A区，C区面积未出错，造成现B区的面积占A、B两区面积和的比例达到了40%．为了协调三个区域的面积占比，爸爸只好将C区面积的40%分成两部分划分给现在的A区和B区．爸爸划分完后，A、B、C三个区域的面积比变为2：1：3，那么爸爸从C区划分给B区的面积与良田总面积的比为．

查看试题解析

三、解答题（66分，17题10分，18-21每题6分，22，23每题10分，24题12分）

17.

(1)、解方程组： ${\begin{array}{l} 5 x - 2 y = 12 \\ 3 x - 4 y = 10 \end{array}$ ．

(2)、解分式方程： $\frac{x - 3}{x - 2} +$ 2 $= \frac{3}{2 - x}$ ．

查看试题解析
18. 计算：

(1)、﹣2ab²•（ $- \frac{1}{2}$ a²b³）² $\div \frac{3}{4}$ a⁵b⁴；

(2)、 $| - 1 | + {(\frac{1}{2})}^{- 1} - {(π - 3.14)}^{0} + {(- 2)}^{3}$

查看试题解析
19. 分解因式：

(1)、4x²﹣100；

(2)、2mx²﹣4mxy+2my.²

查看试题解析
20. 先化简： $\frac{a - 3}{2 a - 4} \div (a + 2 - \frac{5}{a - 2})$ ，再从2，3，4中选择一个符合题意的数作为a的值，并代入求值．

查看试题解析
21. 某中学为了提高学生的综合素质，成立了以下社团：A(机器人)，B(围棋)，C(羽毛球)，D(电影配音)，每人只能加入一个社团，为了解学生参加社团的情况，从参加社团的学生中随机抽取了部分学生进行调查，并将调查结果绘制成两幅不完整的统计图(如图)．根据上述信息，解答下列问题：

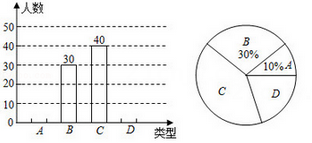
(1)、这次一共调查了多少人?

(2)、求“A”在扇形统计图中所占圆心角的度数；

(3)、请将条形统计图补充完整．

查看试题解析
22. 如图，将△ABC沿射线AB的方向移动2cm到△DEF的位置．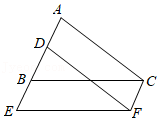

(1)、找出图中所有平行的直线；

(2)、找出图中与AD相等的线段，并写出其长度；

(3)、若∠ABC＝65°，求∠BCF的度数．

查看试题解析
23. 常德市某校购进一批甲、乙两种中考排球，已知一只甲种排球的价格与一只乙种排球的价格的和为40元，用900元购进甲种排球的件数与用1500元购进乙种排球的件数相同．

(1)、求每件甲种、乙种排球的价格分别是多少元？

(2)、该校计划用3500元购买甲、乙两种排球，由于采购人员把甲、乙两种排球的只数互换了，结果需4500元，求该校原计划购进甲、乙两种排球各多少只？

查看试题解析
24. 已知：∠AOB＝α（0°＜α＜90°），一块三角板CDE中，∠CED＝90°，∠CDE＝30°，将三角板CDE如图所示放置，使顶点C落在OB边上，经过点D作直线MN∥OB交OA边于点M，且点M在点D的左侧．

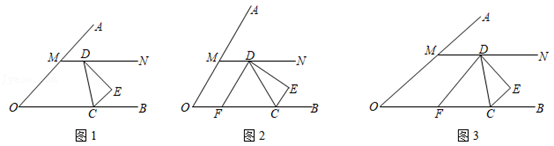(1)、如图1，若CE∥OA，∠NDE＝45°，则α＝°；

(2)、若∠MDC的平分线DF交OB边于点F，
①如图2，当DF∥OA，且α＝60°时，试说明：CE∥OA；

②如图3，当CE∥OA保持不变时，试求出∠OFD与α之间的数量关系．

查看试题解析