浙江省金华市磐安县2021-2022学年九年级下学期期中数学试卷
试卷更新日期:2022-06-16 类型:期中考试
一、选择题(共10小题,共30分)
-
1. -3的倒数是( )A、3 B、±3 C、 D、2. 以下调查中,适宜用全面调查的是( )A、了解全班同学每周体育锻炼的时间 B、调查某批次汽车的抗撞击能力 C、调查春节联欢晚会的收视率 D、全国中学生的视力情况3. 已知二元一次方程组 ,则 的值为( )A、2 B、6 C、4 D、-64. 如图,工人师傅用角尺画出工件边缘 的垂线 和 ,得到 理由是( )
 A、连结直线外一点与直线上各点的所有线段中,垂线段最短 B、在同一平面内,垂直于同一条直线的两条直线互相平行 C、在同一平面内,过一点有一条而且仅有一条直线垂直于已知直线 D、经过直线外一点,有且只有一条直线与这条直线平行5. 实数 , , , , , , (相邻两个3之间依次多一个 1) ,其中无理数的个数是( )A、4 B、2 C、1 D、36. 在平面直角坐标系中,点 与点 关于 轴对称,则( )A、 , B、 , C、 , D、 ,7. 如图,在正方形网格中,点 , , , , 都在格点上.下列说法正确的是( )
A、连结直线外一点与直线上各点的所有线段中,垂线段最短 B、在同一平面内,垂直于同一条直线的两条直线互相平行 C、在同一平面内,过一点有一条而且仅有一条直线垂直于已知直线 D、经过直线外一点,有且只有一条直线与这条直线平行5. 实数 , , , , , , (相邻两个3之间依次多一个 1) ,其中无理数的个数是( )A、4 B、2 C、1 D、36. 在平面直角坐标系中,点 与点 关于 轴对称,则( )A、 , B、 , C、 , D、 ,7. 如图,在正方形网格中,点 , , , , 都在格点上.下列说法正确的是( ) A、点 是 的内心 B、点 是 的外心 C、点 是 的内心 D、点 是 的外心8. 一个物体的三视图如图所示,其中主视图和左视图是全等的等边三角形,俯视图是圆,根据图中所示数据,可求这个物体的表面积为( )
A、点 是 的内心 B、点 是 的外心 C、点 是 的内心 D、点 是 的外心8. 一个物体的三视图如图所示,其中主视图和左视图是全等的等边三角形,俯视图是圆,根据图中所示数据,可求这个物体的表面积为( )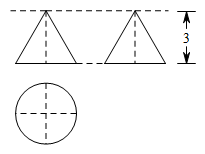 A、 B、 C、 D、9. 如图,四边形 中, , , ,动点 从点 以每秒1个单位长度的速度向点 运动,动点 也同时从点 沿 的路线以每秒2个单位长度的速度向点 运动,当点 到达点 时,点 也随之停止运动,设点 运动的时间为 单位:秒 , 的面积为 ,当 时, 的值为( )
A、 B、 C、 D、9. 如图,四边形 中, , , ,动点 从点 以每秒1个单位长度的速度向点 运动,动点 也同时从点 沿 的路线以每秒2个单位长度的速度向点 运动,当点 到达点 时,点 也随之停止运动,设点 运动的时间为 单位:秒 , 的面积为 ,当 时, 的值为( ) A、 或 B、 或 C、 或 D、 或10. 如图,将正方形纸片 沿 折叠,使点 的对称点 落在边 上,点 的对称点为点 , 交 于点 ,连接 交 于点 ,连接 下列四个结论中:
A、 或 B、 或 C、 或 D、 或10. 如图,将正方形纸片 沿 折叠,使点 的对称点 落在边 上,点 的对称点为点 , 交 于点 ,连接 交 于点 ,连接 下列四个结论中:∽ ; ; 平分 ; ,
其中正确的结论是( )
 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共6小题,共24分)
-
11. 若分式 有意义,则 的取值范围是 .12. 已知 , ,则 .13. 为降低处理成本,减少土地资源消耗,我国正在积极推进垃圾分类政策,引导居民根据“厨余垃圾” 蓝色垃圾桶 、“有害垃圾” 红色垃圾桶 、“可回收物” 绿色垃圾桶 和“其他垃圾” 黑色垃圾桶 这四类标准将垃圾分类处理.爷爷把两袋垃圾随意丢入两个垃圾桶,恰巧被爷爷扔对的概率是.14. 如图,在 中, , ,点 、 分别在 边和 边上,沿着直线 翻折 ,点 落在 边上,记为点 ,如果 ,而且 ,则 .
 15. 若关于 的方程 无解,则 的取值是.16. 如图,在 中, , , , 于 ,与 等长的线段 在边 上沿 方向以 的速度向终点 运动 运动前 与 重合 ,过 , 分别作 的垂线交直角边于 , 两点,设 运动的时间为 .
15. 若关于 的方程 无解,则 的取值是.16. 如图,在 中, , , , 于 ,与 等长的线段 在边 上沿 方向以 的速度向终点 运动 运动前 与 重合 ,过 , 分别作 的垂线交直角边于 , 两点,设 运动的时间为 .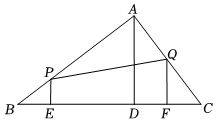 (1)、线段 运动过程中,四边形 成为矩形时 的值;(2)、以 , , 为顶点的三角形与 相似时 的值.
(1)、线段 运动过程中,四边形 成为矩形时 的值;(2)、以 , , 为顶点的三角形与 相似时 的值.三、解答题(本大题共8小题,共66分)
-
17. 计算: .18. 解不等式组: ,把它的解集在数轴上表示出来,并写出其整数解.19. 如图, 中, 、 分别是 、 的中点, ,过点 作 ,交 的延长线于点 .
 (1)、求证:四边形 是菱形.(2)、若 , ,求菱形 的面积.20. 某数学兴趣小组通过调查研究把“如何测量嵩岳寺塔的高度”作为一项课题活动,他们制订了测量方案,并利用课余时间实地测量.
(1)、求证:四边形 是菱形.(2)、若 , ,求菱形 的面积.20. 某数学兴趣小组通过调查研究把“如何测量嵩岳寺塔的高度”作为一项课题活动,他们制订了测量方案,并利用课余时间实地测量.课题
测量嵩岳寺塔的高度
测量工具
测量角度的仪器,皮尺等
测量方案
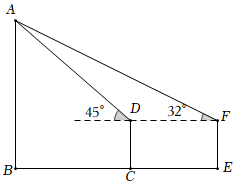
在点 处放置高为 米的测角仪 ,此时测得塔顶端 的仰角为 ,再沿 方向走 米到达点 处,此时测得塔顶端 的仰角为 .
说明: 、 、 三点在同一水平线上
请你根据表中信息结合示意图帮助该数学兴趣小组求嵩岳寺塔 的高度.
精确到0.1米,参考数据: , ,
 21. 某校组织全体1500名学生参加“强国有我”读书活动,要求每人必读 本书,活动结束后从各年级学生中随机抽查了若干名学生了解读书数量情况,并根据 :1本; :2本; :3本; :4本四种类型的人数绘制了不完整的条形统计图 图1)和扇形统计图 图2)请根据统计图解答下列问题:
21. 某校组织全体1500名学生参加“强国有我”读书活动,要求每人必读 本书,活动结束后从各年级学生中随机抽查了若干名学生了解读书数量情况,并根据 :1本; :2本; :3本; :4本四种类型的人数绘制了不完整的条形统计图 图1)和扇形统计图 图2)请根据统计图解答下列问题: (1)、在这次调查中 类型有多少名学生?(2)、直接写出被调查学生读书数量的众数和中位数;(3)、求被调查学生读书数量的平均数,并估计全校1500名学生共读书多少本?22. 如图, 是 的外接圆, 为直径,点 在半圆 上,且与点 在 的异侧, 交 的延长线于点 , .
(1)、在这次调查中 类型有多少名学生?(2)、直接写出被调查学生读书数量的众数和中位数;(3)、求被调查学生读书数量的平均数,并估计全校1500名学生共读书多少本?22. 如图, 是 的外接圆, 为直径,点 在半圆 上,且与点 在 的异侧, 交 的延长线于点 , . (1)、求证: ;(2)、求证: 是 的切线;(3)、若 , ,求 .23. 如图,在平面直角坐标系 中.
(1)、求证: ;(2)、求证: 是 的切线;(3)、若 , ,求 .23. 如图,在平面直角坐标系 中. (1)、直线 分别交 轴、 轴于 、 两点,点 在双曲线 上,过点 分别作 轴、 轴的垂线,交直线 于 、 两点,请直接写出 、 、 、 四点的坐标,并求出 的值.(2)、直线 分别交 轴、 轴于 、 两点,点 在双曲线 上,过点 分别作 轴、 轴的垂线,、交直线 于 、 两点,求 的值.(3)、直线 分别交 轴、 轴于 、 两点,点 在双曲线 上,过点 分别作 轴、 轴的垂线,交直线 于 、 两点,直接写出 的值 用含 的代数式表示 .24. 如图,抛物线 与 轴交于点 , ,与 轴交于点 ,已知 .
(1)、直线 分别交 轴、 轴于 、 两点,点 在双曲线 上,过点 分别作 轴、 轴的垂线,交直线 于 、 两点,请直接写出 、 、 、 四点的坐标,并求出 的值.(2)、直线 分别交 轴、 轴于 、 两点,点 在双曲线 上,过点 分别作 轴、 轴的垂线,、交直线 于 、 两点,求 的值.(3)、直线 分别交 轴、 轴于 、 两点,点 在双曲线 上,过点 分别作 轴、 轴的垂线,交直线 于 、 两点,直接写出 的值 用含 的代数式表示 .24. 如图,抛物线 与 轴交于点 , ,与 轴交于点 ,已知 . (1)、求抛物线的函数表达式;(2)、若点 在 轴上,在该抛物线的对称轴上,是否存在唯一的点 ,满足 ?如果存在,请求出点 的坐标;如果不存在,请说明理由;(3)、若点 在 轴上,满足 的点 是否存在?如果存在,请求出点 的坐标;如果不存在,请说明理由.
(1)、求抛物线的函数表达式;(2)、若点 在 轴上,在该抛物线的对称轴上,是否存在唯一的点 ,满足 ?如果存在,请求出点 的坐标;如果不存在,请说明理由;(3)、若点 在 轴上,满足 的点 是否存在?如果存在,请求出点 的坐标;如果不存在,请说明理由.