浙江省宁波市余姚市2021-2022学年八年级下学期阳明杯学科竞赛(二试)数学试卷
试卷更新日期:2022-06-16 类型:竞赛测试
一、选择题(本题有10个小题,每小题3分,共30分)
-
1. 下列各式中,一定是二次根式的是( ).A、 B、 C、 D、2. 下列关于 的方程是一元二次方程的是( ).A、 B、 C、 D、3. 下面的图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图形的是( ).A、
 科克曲线
B、
科克曲线
B、 笛卡尔心形线
C、
笛卡尔心形线
C、 赵爽弦图
D、
赵爽弦图
D、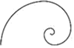 斐波那契螺旋线
4. 在子陵中学“我的中国心”红色主题演讲比赛中,八年级共有 9 位同学参加比赛,这 9位同学决赛成绩各不相同,805 班小张同学想知道自己能否进入前五名,除了要知道自己的成绩之外,还需了解这 9 名同学成绩的( )A、平均数 B、中位数 C、方差 D、标准差5. 用配方法解方程 x2 + 6x -1 = 0 时,配方结果正确的是( )A、(x - 3)2 = 10 B、(x - 3)2 = 8 C、(x + 3)2 = 8 D、(x + 3)2 = 106. 用反证法证明“三角形中至少有一个角不小于60°”,应该先假设这个三角形中( )A、没有一个内角小于60° B、每一个内角小于60° C、至多有一个内角不小于60° D、每一个内角都大于60°7. 如图,小华从点 A 出发向前走 10m,向右转 15°,然后继续向前走 10m,再向右转 15°,他以同样的方法继续走下去,当他第一次回到点 A 时共走了( )米.
斐波那契螺旋线
4. 在子陵中学“我的中国心”红色主题演讲比赛中,八年级共有 9 位同学参加比赛,这 9位同学决赛成绩各不相同,805 班小张同学想知道自己能否进入前五名,除了要知道自己的成绩之外,还需了解这 9 名同学成绩的( )A、平均数 B、中位数 C、方差 D、标准差5. 用配方法解方程 x2 + 6x -1 = 0 时,配方结果正确的是( )A、(x - 3)2 = 10 B、(x - 3)2 = 8 C、(x + 3)2 = 8 D、(x + 3)2 = 106. 用反证法证明“三角形中至少有一个角不小于60°”,应该先假设这个三角形中( )A、没有一个内角小于60° B、每一个内角小于60° C、至多有一个内角不小于60° D、每一个内角都大于60°7. 如图,小华从点 A 出发向前走 10m,向右转 15°,然后继续向前走 10m,再向右转 15°,他以同样的方法继续走下去,当他第一次回到点 A 时共走了( )米.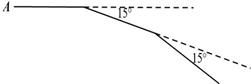 A、200 米 B、240 米 C、280 米 D、300 米8. 某商店经销一种销售成本为40元的水果,据市场分析,若按每千克50元销售,一个月能售出500千克:销售单价每涨1元,月销售量就减少10千克,设销售单价为每千克x(x>50)元,月销售利润达8000元.则方程为( )A、(x﹣40)[500﹣10(x﹣50)]=8000 B、(x﹣40)(10x﹣500)=8000 C、(x﹣40)(500﹣10x)=8000 D、(x﹣40)[500﹣10(50﹣x)]=80009. 已知点A(x1 , y1),B(x2 , y2),C(x3 , y3)都在反比例函数 (a是常数)的图象上,且y1<y2<0<y3 , 则x1 , x2 , x3的大小关系为( )A、x2>x1>x3 B、x3>x1>x2 C、x3>x2>x1 D、x1>x2>x310. 如图所示,在矩形纸片ABCD中,AB=3,BC=6,点E、F分别是矩形的边AD、BC上的动点,将该纸片沿直线EF折叠.使点B落在矩形边AD上,对应点记为点G,点A落在M处,连接EF、BG、BE,EF与BG交于点N.则下列结论成立的是( )
A、200 米 B、240 米 C、280 米 D、300 米8. 某商店经销一种销售成本为40元的水果,据市场分析,若按每千克50元销售,一个月能售出500千克:销售单价每涨1元,月销售量就减少10千克,设销售单价为每千克x(x>50)元,月销售利润达8000元.则方程为( )A、(x﹣40)[500﹣10(x﹣50)]=8000 B、(x﹣40)(10x﹣500)=8000 C、(x﹣40)(500﹣10x)=8000 D、(x﹣40)[500﹣10(50﹣x)]=80009. 已知点A(x1 , y1),B(x2 , y2),C(x3 , y3)都在反比例函数 (a是常数)的图象上,且y1<y2<0<y3 , 则x1 , x2 , x3的大小关系为( )A、x2>x1>x3 B、x3>x1>x2 C、x3>x2>x1 D、x1>x2>x310. 如图所示,在矩形纸片ABCD中,AB=3,BC=6,点E、F分别是矩形的边AD、BC上的动点,将该纸片沿直线EF折叠.使点B落在矩形边AD上,对应点记为点G,点A落在M处,连接EF、BG、BE,EF与BG交于点N.则下列结论成立的是( )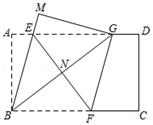
①BN=AB;②当点G与点D重合时,EF= ;③△GNF的面积S的取值范围是
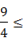 ;④当CF= 时,S△MEG=
;④当CF= 时,S△MEG= 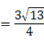 .A、①③ B、③④ C、②③ D、②④
.A、①③ B、③④ C、②③ D、②④二、填空题(本题有6小题,每小题4分,共24分)
-
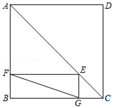
11. 要使二次根式 有意义,则x的取值范围是 .12. 已知一组数据 , , 的平均数和方差分别是2, ,那么另一组数据 ,2 , 的平均数和方差分别是 , .13. 已知关于 x 的一元二次方程 k2x2 - (2k +1)x +1 = 0 有两个实数根,则 k 的取值范围是14. 如图,在正方形ABCD中,点E在对角线AC上,EF⊥AB于点F,EG⊥BC于点G,连接FG,若AB=8,则FG的最小值为 .
 15. 如图,在四边形ABCD中,∠A=90°,AB=AD,E、F分别是 AB、AD 中点,若EF= ,BC= ,CD= ,则 S四边形 ABCD=.
15. 如图,在四边形ABCD中,∠A=90°,AB=AD,E、F分别是 AB、AD 中点,若EF= ,BC= ,CD= ,则 S四边形 ABCD=.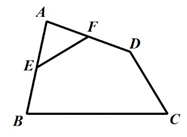 16. 如图是8个台阶的示意图,每个台阶的高和宽分别是2和3,每个台阶凸出的角的顶点记作Tm(m为1~8的整数).反比例函数y (x>0)的图象为曲线L.
16. 如图是8个台阶的示意图,每个台阶的高和宽分别是2和3,每个台阶凸出的角的顶点记作Tm(m为1~8的整数).反比例函数y (x>0)的图象为曲线L.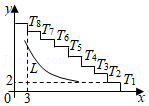 (1)、若反比例函数的图象L过点T1 , 则k=;(2)、若反比例函数图象L使得T1~T8这些点分布在它的两侧,每侧各4个点,则k的整数值有个.
(1)、若反比例函数的图象L过点T1 , 则k=;(2)、若反比例函数图象L使得T1~T8这些点分布在它的两侧,每侧各4个点,则k的整数值有个.三、解答题(第17、18、19题各6分,第20、21题各8分,第22、23题10分,第24题12分,共66分)
-
17. 计算:(1)、(2)、18. 解方程:(1)、x2﹣2x﹣15=0;(2)、(3x+2)2=3(3x+2).19. 我们把每个顶点都在格点的四边形叫做格点四边形.如图,在所给的 方格纸中,点A,B均为格点,请画出符合要求的格点四边形.
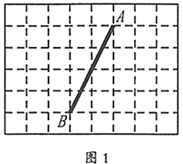
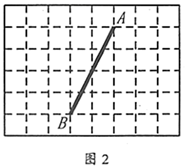 (1)、在图1中画出一个以 为边的矩形 ,且它的面积为整数;(2)、在图2中画出一个以 为对角线的菱形 ,且它的周长为整数.20. 2020新型冠状病毒突然来袭,我校为了增强同学们的科学防疫意识,开展了以“科学防疫,我健康,我快乐”为主题的安全知识竞赛,并从全校学生中随机抽取了男、女同学各40名,并将数据进行整理分析,得到了如下信息:
(1)、在图1中画出一个以 为边的矩形 ,且它的面积为整数;(2)、在图2中画出一个以 为对角线的菱形 ,且它的周长为整数.20. 2020新型冠状病毒突然来袭,我校为了增强同学们的科学防疫意识,开展了以“科学防疫,我健康,我快乐”为主题的安全知识竞赛,并从全校学生中随机抽取了男、女同学各40名,并将数据进行整理分析,得到了如下信息: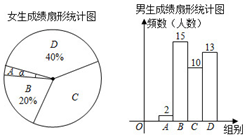
(1)女生成绩扇形统计图和男生成绩频数分布直方图如图:(数据分组为 组: , 组: , 组: , 组: )
(2)女生 组中全部15名学生的成绩为:86,87,81,83,89,84,85,87,86,89,82,88,89,85,89(3)两组数据的相关统计数据如表 (单位:分 )
平均数
中位数
众数
满分率
女生
90
25%
男生
90
88
98
15%
(1)、扇形统计图中 组学生对应的圆心角 的度数为度,认真分析以上数据信息后填空:中位数 , 众数 ;(2)、通过以上的数据分析,你认为 ▲ (填“女生”或“男生” )知识竞赛成绩更好,并说明理由;(3)、若成绩在90分 (包含90分 )以上为优秀,请你估计我校2400名学生此次知识竞赛中优秀的人数.21. 直线y=3x与反比例函数y= 的图象交于A(1,m)和点B.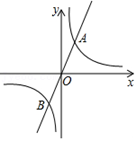 (1)、求m、k的值,并直接写出点B的坐标(2)、过点P(t,0)(﹣1≤t≤1且t≠0)作x轴的垂线分别交直线y=3x与反比例函数y= 的图象于点E,F.
(1)、求m、k的值,并直接写出点B的坐标(2)、过点P(t,0)(﹣1≤t≤1且t≠0)作x轴的垂线分别交直线y=3x与反比例函数y= 的图象于点E,F.①当t= 时,求线段EF的长;
②若0<EF≤8,请根据图象直接写出t的取值范围.22. 如图,已知△ABC中,D是AC的中点,过点D作DE⊥AC交BC于点E,过点A作AF∥BC交DE于点F,连接AE、CF.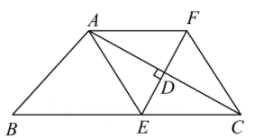 (1)、求证:四边形AECF是菱形;(2)、若CF=2,∠FAC=30°,∠B=45°,求AB的长.23. 某商场在去年底以每件80元的进价购进一批同型号的服装,一月份以每件150元的售价销售了320件,二、三月份该服装畅销,销量持续走高,在售价不变的情况下,三月底统计知三月份的销量达到了500件(1)、求二、三月份服装销售量的平均月增长率(2)、从四月份起商场因换季清仓采用降价促销的方式,经调查发现,在三月份销量的基础上,该服装售价每降价5元,月销售量增加10件,当每件降价多少元时,四月份可获利12000元?24. 在平行四边形ABCD中,∠BAD=α,DE平分∠ADC,交对角线AC于点G,交射线AB于点E,将线段EB绕点E顺时针旋转 α得线段EP.
(1)、求证:四边形AECF是菱形;(2)、若CF=2,∠FAC=30°,∠B=45°,求AB的长.23. 某商场在去年底以每件80元的进价购进一批同型号的服装,一月份以每件150元的售价销售了320件,二、三月份该服装畅销,销量持续走高,在售价不变的情况下,三月底统计知三月份的销量达到了500件(1)、求二、三月份服装销售量的平均月增长率(2)、从四月份起商场因换季清仓采用降价促销的方式,经调查发现,在三月份销量的基础上,该服装售价每降价5元,月销售量增加10件,当每件降价多少元时,四月份可获利12000元?24. 在平行四边形ABCD中,∠BAD=α,DE平分∠ADC,交对角线AC于点G,交射线AB于点E,将线段EB绕点E顺时针旋转 α得线段EP.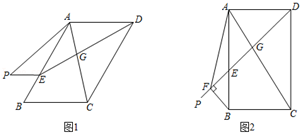 (1)、如图1,当α=120°时,连接AP,请写出线段AP和线段AC的数量关系,并说明理由;(2)、如图2,当α=90°时,过点B作BF⊥EP于点F,连接AF,请写出线段AF,AB,AD之间的数量关系,并说明理由;(3)、当α=120°时,连接AP,若BE AB,直接写出△APE与△CDG面积的比值.
(1)、如图1,当α=120°时,连接AP,请写出线段AP和线段AC的数量关系,并说明理由;(2)、如图2,当α=90°时,过点B作BF⊥EP于点F,连接AF,请写出线段AF,AB,AD之间的数量关系,并说明理由;(3)、当α=120°时,连接AP,若BE AB,直接写出△APE与△CDG面积的比值.