山东省泰安市高新区2020-2021学年第二学期(五四学制)六年级数学期中考试试题
试卷更新日期:2022-06-16 类型:期中考试
一、选择题
-
1. 把一条弯曲的河道改成直道,可以缩短航程,其中的道理可以解释为( )A、两点确定一条直线 B、两点之间,直线最短 C、两点之间,线段最短 D、线段可以比较大小2. 下列各题的计算,正确的是( )A、(a2)3=a5 B、(-3a2)3=-9a6 C、(-a)·(-a)6=-a7 D、a3+a3=2a63. 2020年6月23日,我国成功发射了北斗系统第55颗导航卫星,其授时精度为世界之最,不超过0.000000009秒.将数据“0.0000000099”用科学记数法表示为( )A、99×10-10 B、9.9×10-9 C、9.9×10-10 D、9.9×10-84. 如图,钟表上显示的时间是12:20,此时,时针与分针的夹角是( )
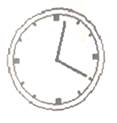 A、100° B、110° C、115° D、120°5. 在下列多项式的乘法中,可以用平方差公式计算的是( )A、(2x+y)(2y-x) B、( x+1)( x-1) C、(-3x-y)(3x+y) D、(-2x- y)(2x-y)6. 如图,OC平分∠AOB,OD平分∠AOC,∠AOD=40°,则∠AOB的度数是( )
A、100° B、110° C、115° D、120°5. 在下列多项式的乘法中,可以用平方差公式计算的是( )A、(2x+y)(2y-x) B、( x+1)( x-1) C、(-3x-y)(3x+y) D、(-2x- y)(2x-y)6. 如图,OC平分∠AOB,OD平分∠AOC,∠AOD=40°,则∠AOB的度数是( )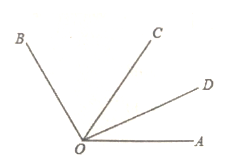 A、160° B、120° C、80° D、60°7. 计算(-1.5)2020×( )2021的结果是( )A、 B、 C、 D、8. 若2a=5,2b=3,则22a-3b等于( )A、 B、 C、 D、9. 若多项式x2+kx+81是一个整式的完全平方,则k的值为( )A、18 B、-18 C、±18 D、±910. 如图,点E在AC的延长线上,下列条件中不能判断AB∥CD的是( )
A、160° B、120° C、80° D、60°7. 计算(-1.5)2020×( )2021的结果是( )A、 B、 C、 D、8. 若2a=5,2b=3,则22a-3b等于( )A、 B、 C、 D、9. 若多项式x2+kx+81是一个整式的完全平方,则k的值为( )A、18 B、-18 C、±18 D、±910. 如图,点E在AC的延长线上,下列条件中不能判断AB∥CD的是( )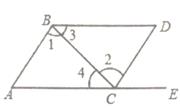 A、∠A=∠DCE B、∠1=∠2 C、∠3=∠4 D、∠D+∠ABD=180°11. 如图,AB∥CD,CD⊥EF,若∠1=125°,则∠2=( )
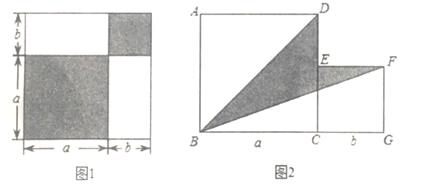
A、∠A=∠DCE B、∠1=∠2 C、∠3=∠4 D、∠D+∠ABD=180°11. 如图,AB∥CD,CD⊥EF,若∠1=125°,则∠2=( )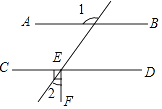 A、25° B、35° C、55° D、65°12. 如图的分割正方形,拼接成长方形方案中,可以验证( )
A、25° B、35° C、55° D、65°12. 如图的分割正方形,拼接成长方形方案中,可以验证( ) A、(a+b)2=a2+2ab+b2 B、(a-b)2=a2-2ab+b2 C、(a+b)2=(a+b)2-4ab D、a2-b2=(a+b)(a-b)
A、(a+b)2=a2+2ab+b2 B、(a-b)2=a2-2ab+b2 C、(a+b)2=(a+b)2-4ab D、a2-b2=(a+b)(a-b)二、填空题
-
13. 已知∠A=21°32',则∠A的补角度数为14. 如图,点C是线段AB上的点,点M、N分别是AC、BC的中点,若AC=6cm,MN=5cm,则线段MB=cm.
 15. 小明的妈妈把一个月的家庭支出情况,用如图所示的扇形统计图来表示,则教育所占扇形的圆心角的度数是
15. 小明的妈妈把一个月的家庭支出情况,用如图所示的扇形统计图来表示,则教育所占扇形的圆心角的度数是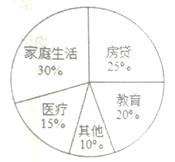 16. 已知m2-4n2=16,m+2n=5,则m-2n= .17. 在平面内,将一个直角三角板按如图所示摆放在一组平行线上,若∠1=55°,则∠2的度数是
16. 已知m2-4n2=16,m+2n=5,则m-2n= .17. 在平面内,将一个直角三角板按如图所示摆放在一组平行线上,若∠1=55°,则∠2的度数是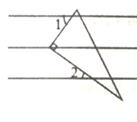 18. 柳林乡要修建一条灌溉水渠,如图,水渠从A村沿北偏东63°方向到B村,从B村沿北偏西27°方向到C村,水渠从C村沿北偏东方向修建, 可以保持AB的方向一致。
18. 柳林乡要修建一条灌溉水渠,如图,水渠从A村沿北偏东63°方向到B村,从B村沿北偏西27°方向到C村,水渠从C村沿北偏东方向修建, 可以保持AB的方向一致。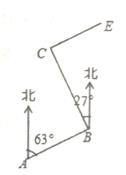 19. 计算(1)、3ab·(-2ab)+(-3a2b)2(2)、(25m2+15m2n-20m)÷(-5m2)(3)、0.25×(-2)2+16-1-(π-3)0(4)、(a+2b+c)(a+2b-c)20. 按要求解下列各题(1)、先化简,再求值:(x-2y)2-3(x+y)(x-y)+2x2 , 其中,x=1,y=-1.(2)、解方程:(3x-2)(2x-3)=(6x+5)(x-1)-1.21. 如图,线段AB,C是线段AB上一点,M是AB的中点,N是AC的中点.若 , ,求线段MN的长;
19. 计算(1)、3ab·(-2ab)+(-3a2b)2(2)、(25m2+15m2n-20m)÷(-5m2)(3)、0.25×(-2)2+16-1-(π-3)0(4)、(a+2b+c)(a+2b-c)20. 按要求解下列各题(1)、先化简,再求值:(x-2y)2-3(x+y)(x-y)+2x2 , 其中,x=1,y=-1.(2)、解方程:(3x-2)(2x-3)=(6x+5)(x-1)-1.21. 如图,线段AB,C是线段AB上一点,M是AB的中点,N是AC的中点.若 , ,求线段MN的长;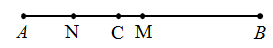 22. 如图所示,AB为一条直线,OC是∠AOD的平分线,OE在∠BOD内,∠AOC=30° ,∠BOE=2∠DOE,求∠BOE的度数。
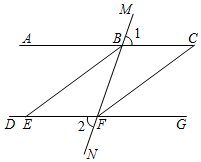
22. 如图所示,AB为一条直线,OC是∠AOD的平分线,OE在∠BOD内,∠AOC=30° ,∠BOE=2∠DOE,求∠BOE的度数。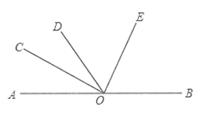 23. 已知:如图,直线AB∥CD,BC平分∠ABD,∠1=50°,求∠2的度数.
23. 已知:如图,直线AB∥CD,BC平分∠ABD,∠1=50°,求∠2的度数.