山东省泰安市肥城市(五四制)2020-2021学年六年级下学期期中教学质量监测数学试题
试卷更新日期:2022-06-16 类型:期中考试
一、 选择题
-
1. 下列运算正确的是( )A、3xy-xy=2 B、x'3·x4=x12 C、2x3÷x2=x D、(-x3)2=x62. 如图,OC是∠AOB的平分线,OD是∠BOC的平分线,那么下列各式中正确的是( )
 A、∠COD= ∠AOB B、∠AOD= ∠AOB C、∠BOD = ∠AOD D、∠BOC= ∠AOB3. 世界上最小的开花结果植物是澳大利亚的出水浮萍,这种植物的果实像一个微小的无花果,质量只有0.000000076克,用科学记数法表示这个质量是( )A、7.6×108 克 B、7.6×10-7克 C、7.6×10-8克 D、7.6×10-9克4. 如图,直线a∥b,∠1=50°,∠2=30°,则∠3的度数为( )
A、∠COD= ∠AOB B、∠AOD= ∠AOB C、∠BOD = ∠AOD D、∠BOC= ∠AOB3. 世界上最小的开花结果植物是澳大利亚的出水浮萍,这种植物的果实像一个微小的无花果,质量只有0.000000076克,用科学记数法表示这个质量是( )A、7.6×108 克 B、7.6×10-7克 C、7.6×10-8克 D、7.6×10-9克4. 如图,直线a∥b,∠1=50°,∠2=30°,则∠3的度数为( )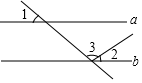 A、40° B、90° C、50° D、100°5. 下列说法错误的是( )A、直线AB和直线BA是同一条直线 B、若线段AB=5,AC=3,则BC不可能是1 C、画一条5厘米长的线段 D、若线段AM=2,BM=2,则M为线段AB的中点6. 如图,正方形卡片A类,B类和长方形卡片C类若干张,如果要拼一个长为(a+2b),宽为(3a+b)的大长方形,则需要C类卡片的张数为( )
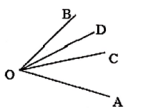
A、40° B、90° C、50° D、100°5. 下列说法错误的是( )A、直线AB和直线BA是同一条直线 B、若线段AB=5,AC=3,则BC不可能是1 C、画一条5厘米长的线段 D、若线段AM=2,BM=2,则M为线段AB的中点6. 如图,正方形卡片A类,B类和长方形卡片C类若干张,如果要拼一个长为(a+2b),宽为(3a+b)的大长方形,则需要C类卡片的张数为( )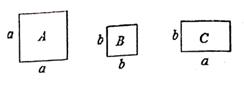 A、5张 B、6张 C、7张 D、8张7. 如图:已知AB∥CD,∠B=120°,∠D=150°,则∠O等于( )
A、5张 B、6张 C、7张 D、8张7. 如图:已知AB∥CD,∠B=120°,∠D=150°,则∠O等于( )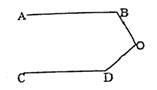 A、50° B、90° C、80° D、60°8. 将一个圆分割成三个扇形,它们的圆心角的度数之比为2:3:4,则这些扇形圆心角的度数分别为( )A、30°,60°,90° B、60°,120°,180° C、50°,100°,150° D、80°,120°,160°9. 如果m2+m=5,那么代数式m(m-2)+(m+2)2的值为( )A、14 B、9 C、-1 D、-610. 已知 , ,则 的值是( )A、64 B、52 C、50 D、2811. 若x2+2(m-3)x+1是完全平方式,x+n与x+2的乘积中不含x的一次项,则nm的值为( )A、-4 B、16 C、4或16 D、-4或-1612. “创卫工作, 人人参与”,我市园林工作者,为了把城市装扮得更加靓丽,用若干相同的花盆按一定的规律组成不同的正多边形图案,如图,其中第1个图形是正三角形图案,一共有6个花盆,第2个图形是正方形图案,一共有12个花盆,第3个图形是正五边
A、50° B、90° C、80° D、60°8. 将一个圆分割成三个扇形,它们的圆心角的度数之比为2:3:4,则这些扇形圆心角的度数分别为( )A、30°,60°,90° B、60°,120°,180° C、50°,100°,150° D、80°,120°,160°9. 如果m2+m=5,那么代数式m(m-2)+(m+2)2的值为( )A、14 B、9 C、-1 D、-610. 已知 , ,则 的值是( )A、64 B、52 C、50 D、2811. 若x2+2(m-3)x+1是完全平方式,x+n与x+2的乘积中不含x的一次项,则nm的值为( )A、-4 B、16 C、4或16 D、-4或-1612. “创卫工作, 人人参与”,我市园林工作者,为了把城市装扮得更加靓丽,用若干相同的花盆按一定的规律组成不同的正多边形图案,如图,其中第1个图形是正三角形图案,一共有6个花盆,第2个图形是正方形图案,一共有12个花盆,第3个图形是正五边形图案,一共有20个花盆,……,则第8个图形中一共有花盆的个数为( )
 A、56 B、64 C、72 D、90
A、56 B、64 C、72 D、90二、填空题
-
13. 如果∠AOB=55°,过O点有一条射线OC,使∠AOC=15°,那么∠BOC的度数是14. 计算(-1.5)2021×( )2020的结果是15. 将一张长方形纸片按如图所示的方式折叠,BD、BE为折痕,若∠CBD=66° ,则∠ABE=
 16. 一副三角板如图摆放,且AB∥CD,则∠1的度数为
16. 一副三角板如图摆放,且AB∥CD,则∠1的度数为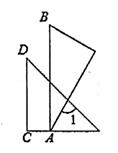 17. 若(y+3)0无意义,且3x+2y=9,则yx=18. 南宋数学家杨辉在其著作《详解九章算法》中揭示了(a+b)n(n为非负整数)展开式的项数及各项系数的有关规律如下,后人也将下表称为“杨辉三角”
17. 若(y+3)0无意义,且3x+2y=9,则yx=18. 南宋数学家杨辉在其著作《详解九章算法》中揭示了(a+b)n(n为非负整数)展开式的项数及各项系数的有关规律如下,后人也将下表称为“杨辉三角”
(a+b)0=1
(a+b)1=a+b
(a+b)2=a2+2ab+b2
(a+b)3=a3+3a2b+3ab2+b3
(a+b)4=a4+4a3b+6a2b2+4ab3+b4
则(a+b)8展开式中所有项的系数的和是
三、解答题(解答题要写出必要的步骤)
-
19. 计算:(1)、180°-(34°55'+21°33'(2)、( )-2+(2021-π)0-(-3)3;(3)、(-4am+1)3÷[2(2am)2·a](4)、(2x+y)2+(x+y)(x-y)-5x(x-y).20. 先化简,再求值:(1)、[(x+2y)2-(x+y)(3x-y)-5y]÷( x),其中x=-2,y=(2)、(2a-b)2-(a+1-b)(a+1+b)+(a+1)2 , 其中a、b满足关系式:(a+3)2+|b-1|=021. 如图,已知线段AB和CD的公共部分BD= AB= CD,线段AB、CD的中点E,F之间距离是10cm,求AB,CD的长.
 22. 已知直线AB和CD相交于点O,∠COE是真角,OF平分∠AOE.
22. 已知直线AB和CD相交于点O,∠COE是真角,OF平分∠AOE.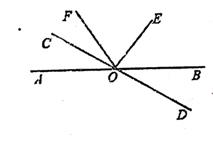 (1)、写出∠AOC与∠BOD的大小关系,并说明理由;(2)、若∠COF=35°,求∠BOD的度数.23. 发现与探索
(1)、写出∠AOC与∠BOD的大小关系,并说明理由;(2)、若∠COF=35°,求∠BOD的度数.23. 发现与探索你能求(x-1)(x2020+x2019+x2018+……+x+1)的值吗?
遇到这样的问题,我们可以先思考一下,从简单的情形入手.先分别计算下列各式的值:
①(x-1)(x+1)=x2-1;
②(x-1)(x2+x+1)=x3-1;
③(x-1) (x3+x2+x+1)=x4-1;
(1)、猜想(x-1)(x2020+x2019+x2018+……+x+1)的结果;请你利用上面的结论,完成下面的题目的计算:
(2)、32020+32019+32018+……+3+1;24. 如图,已知点A在EF上,点P,Q在BC上,∠E=∠EMA,∠BQM=∠BMQ.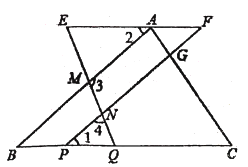 (1)、EF与BC平行吗?请说明理由;(2)、若∠3+∠4=180°,∠BAF=3∠F-20°,求∠B的度数.
(1)、EF与BC平行吗?请说明理由;(2)、若∠3+∠4=180°,∠BAF=3∠F-20°,求∠B的度数.