广东省2022年初中学业水平数学第二次模拟考试
试卷更新日期:2022-06-16 类型:中考模拟
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的选项中,只有一项是符合题目要求的)
-
1. 在
 ,
,  ,0,-2这四个数中,为无理数的是( ) A、
,0,-2这四个数中,为无理数的是( ) A、 B、
B、 C、0
D、-2
2. 若a-b=2,b-c=-3,则a-c等于( )A、1 B、-1 C、5 D、-53. 2022年第11期某市小汽车增量调控竞价结束,个人车牌平均成交价约为86000元,86000用科学记数法表示应为( )A、86×103 B、8.6×104 C、8.6×105 D、0.86x1054. 下列等式成立的是( )A、 B、 C、 D、5. 下面图形中,既是轴对称图形又是中心对称图形的是( )A、
C、0
D、-2
2. 若a-b=2,b-c=-3,则a-c等于( )A、1 B、-1 C、5 D、-53. 2022年第11期某市小汽车增量调控竞价结束,个人车牌平均成交价约为86000元,86000用科学记数法表示应为( )A、86×103 B、8.6×104 C、8.6×105 D、0.86x1054. 下列等式成立的是( )A、 B、 C、 D、5. 下面图形中,既是轴对称图形又是中心对称图形的是( )A、 B、
B、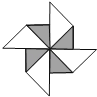 C、
C、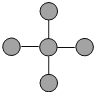 D、
D、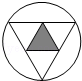 6. 如图,直线l1∥I2 , 以点A为圆心,适当长为半径画弧,分别交l1 , l2于B,C两点,连接AC,BC.若∠ABC=54°,则∠1的大小为( )
6. 如图,直线l1∥I2 , 以点A为圆心,适当长为半径画弧,分别交l1 , l2于B,C两点,连接AC,BC.若∠ABC=54°,则∠1的大小为( ) A、36° B、54° C、72° D、73°7. 下列计算中,正确的是( )A、 B、 C、 D、8. 某轨道列车共有3节车厢,设乘客从任意一节车厢上车的机会均等。某天甲、乙两位乘客同时乘同一列轨道列车,则甲和乙从同一节车厢上车的概率是( )A、 B、 C、 D、9. 关于x的不等式x-b>0恰有两个负整数解,则b的取值范围是( )A、-3<b<-2 B、-3<b≤-2 C、-3≤b≤-2 D、-3≤b<-210. 如图,在矩形ABCD中,AB=6,BC=4,点E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连接AP并延长AP交CD于点F.下列结论中,正确的结论有( )
A、36° B、54° C、72° D、73°7. 下列计算中,正确的是( )A、 B、 C、 D、8. 某轨道列车共有3节车厢,设乘客从任意一节车厢上车的机会均等。某天甲、乙两位乘客同时乘同一列轨道列车,则甲和乙从同一节车厢上车的概率是( )A、 B、 C、 D、9. 关于x的不等式x-b>0恰有两个负整数解,则b的取值范围是( )A、-3<b<-2 B、-3<b≤-2 C、-3≤b≤-2 D、-3≤b<-210. 如图,在矩形ABCD中,AB=6,BC=4,点E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连接AP并延长AP交CD于点F.下列结论中,正确的结论有( )
①BP⊥AP;②BP·EC= PC·AB;③13S△ABP=12S四边形PBCF ;④sin∠PCF=
A、4 B、3 C、2 D、1二、填空题(本大题共7小题,每小题4分,共28分.请把答案填在答题卡相应位置上)
-
11. 分式方程 的根为 .12.
如图,在正方形ABCD中,如果AF=BE,那么∠AOD的度数是 .
 13. 分解因式a3-6a2 +9a= .14. 如图,数轴上点A表示的数为a,化简: =
13. 分解因式a3-6a2 +9a= .14. 如图,数轴上点A表示的数为a,化简: =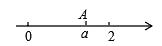 15. 如图,在矩形ABCD中,AB=3,AD=5,点E在DC上,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,那么cos∠EFC的值是 .
15. 如图,在矩形ABCD中,AB=3,AD=5,点E在DC上,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,那么cos∠EFC的值是 .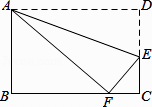 16. 如图,AB是⊙O的直径,点C,D在圆上,∠D=68°,则∠ABC=
16. 如图,AB是⊙O的直径,点C,D在圆上,∠D=68°,则∠ABC= 17. 如图,∠AOB=30°,点M,N分别在边0A,OB上,且OM=1,ON=3,点P,Q分别在边OB,OA上,则MP+PQ+QN的最小值是
17. 如图,∠AOB=30°,点M,N分别在边0A,OB上,且OM=1,ON=3,点P,Q分别在边OB,OA上,则MP+PQ+QN的最小值是
三、解答题(本大题共3小题,每小题6分,共18分)
-
18. 解方程组:19. 某市体育中考共设跳绳、立定跳远、仰卧起坐三个项目,要求每位学生必须且只需选考其中一项,该市某中学九(1)班学生选考三个项目的人数分布的条形统计图和扇形统计图如图所示.
 (1)、求该班的学生人数;(2)、若该校九年级共有1000人,估计该年级选考立定跳远的人数.20. 如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C.求证:BD=CE.
(1)、求该班的学生人数;(2)、若该校九年级共有1000人,估计该年级选考立定跳远的人数.20. 如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C.求证:BD=CE.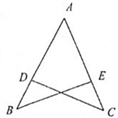
四、解答题(本大题共3小题,每小题8分,共24分)
-
21. 如图,一根电线杆PQ直立在山坡上,从地面的点A看,测得杆顶端点P的仰角为45°,向前走6m到达点B,又测得杆顶端点P和杆底端点Q的仰角分别为60°和30°.
 (1)、求证:△BPQ是等腰三角形;(2)、求电线杆PQ的高度,(结果精确到1m,参考数据: ≈1.41, ≈1.73, ≈2.24)22. 如图,直线AB与反比例函数y= (k≠0)的图象相交于A,B两点,已知A(1,4).
(1)、求证:△BPQ是等腰三角形;(2)、求电线杆PQ的高度,(结果精确到1m,参考数据: ≈1.41, ≈1.73, ≈2.24)22. 如图,直线AB与反比例函数y= (k≠0)的图象相交于A,B两点,已知A(1,4). (1)、求反比例函数的解析式;(2)、直线AB交x轴于点C,连接OA,当△AOC的面积为6时,求直线AB的解析式,23. 如图,已知BD垂直平分线段AC,∠BCD=∠ADF,AF⊥AC
(1)、求反比例函数的解析式;(2)、直线AB交x轴于点C,连接OA,当△AOC的面积为6时,求直线AB的解析式,23. 如图,已知BD垂直平分线段AC,∠BCD=∠ADF,AF⊥AC (1)、证明:四边形ABDF是平行四边形;(2)、若AF=DF=5,AD=6,求AC的长.
(1)、证明:四边形ABDF是平行四边形;(2)、若AF=DF=5,AD=6,求AC的长.五、解答题三(本大题共2小题,每小题10分,共20分)
-
24. 在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线交BC于点E.
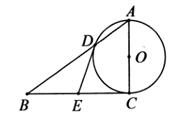 (1)、求证:点E是边BC的中点;(2)、求证:BC2=BD·BA;(3)、当以点O,D,E,C为顶点的四边形是正方形时,求证:△ABC是等腰直角三角形.25. 已知抛物线y= x2+c与x轴交于A(-1,0),B两点,交y轴于点C.
(1)、求证:点E是边BC的中点;(2)、求证:BC2=BD·BA;(3)、当以点O,D,E,C为顶点的四边形是正方形时,求证:△ABC是等腰直角三角形.25. 已知抛物线y= x2+c与x轴交于A(-1,0),B两点,交y轴于点C. (1)、求抛物线的解析式;(2)、点E(m,n)是第二象限内一点,过点E作EK⊥x轴于点K,线段EK交抛物线于点F,过点F作FG⊥y轴于点G,连接CE,CF,若∠CEF=∠CFG,求n的值并直接写出m的取值范围.(利用图1完成你的探究);(3)、如图2,点P是线段OB上一动点(不包括点O,B),PM⊥x轴交抛物线于点M,∠OBQ=∠OMP,BQ交直线PM于点Q,设点P的横坐标为t,求△PBQ的周长.
(1)、求抛物线的解析式;(2)、点E(m,n)是第二象限内一点,过点E作EK⊥x轴于点K,线段EK交抛物线于点F,过点F作FG⊥y轴于点G,连接CE,CF,若∠CEF=∠CFG,求n的值并直接写出m的取值范围.(利用图1完成你的探究);(3)、如图2,点P是线段OB上一动点(不包括点O,B),PM⊥x轴交抛物线于点M,∠OBQ=∠OMP,BQ交直线PM于点Q,设点P的横坐标为t,求△PBQ的周长.