河北省沧州市2022届高三数学模拟测试卷

试卷更新日期：2022-06-15 类型：高考模拟

进入出卷网下载

一、单选题

1. 复数 ${(\frac{1 - i}{1 + i})}^{2022} =$ （）

A、i B、-i C、1 D、-1

查看试题解析
2. 设集合P，Q均为全集U的非空子集，且 $P ∩ (∁_{U} Q) = P$ ，则 $(∁_{U} P) ∩ Q =$ （）

A、P B、Q C、 $\emptyset$ D、 $U$

查看试题解析
3. 设 $f (x)$ 是定义域为 $R$ 的偶函数，且在 $(0, + \infty)$ 单调递减，则（）

A、 $f (\log_{3} \frac{1}{4}) > f (2^{- \frac{3}{2}}) > f (2^{- \frac{2}{3}})$ B、 $f (\log_{3} \frac{1}{4}) > f (2^{- \frac{2}{3}}) > f (2^{- \frac{3}{2}})$ C、 $f (2^{- \frac{3}{2}}) > f (2^{- \frac{2}{3}}) > f (\log_{3} \frac{1}{4})$ D、 $f (2^{- \frac{2}{3}}) > f (2^{- \frac{3}{2}}) > f (\log_{3} \frac{1}{4})$

查看试题解析
4. 下列图象对应的函数解析式正确的是（）

A、 $f (x) = x c o s x$ B、 $f (x) = x s i n x$ C、 $f (x) = x s i n x + c o s x$ D、 $f (x) = x c o s x + s i n x$

查看试题解析
5. $\frac{\sqrt{3}}{s i n \frac{π}{9}} - \frac{1}{s i n (- \frac{97 π}{18})} =$ （）

A、3 B、4 C、 $\frac{4 \sqrt{3}}{3}$ D、 $\frac{5 \sqrt{3}}{3}$

查看试题解析
6. 已知双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左右焦点分别为F₁ ， F₂ ，右顶点为A，M为OA的中点，P为双曲线C右支上一点且 $P F_{2} ⊥ F_{1} F_{2}$ ，且 $t a n ∠ P F_{1} F_{2} = \frac{3}{4}$ ，则说法错误的是（）

A、C的离心率为2 B、C的渐近线方程为 $x \pm \sqrt{3} y = 0$ C、PM平分 $∠ F_{1} P F_{2}$ D、 $\vec{P A} = \frac{1}{4} \vec{P F_{1}} + \frac{3}{4} \vec{P F_{2}}$

查看试题解析
7. 河南洛阳的龙门石窟是中国石刻艺术宝库之一，现为世界文化遗产，龙门石窟与莫高窟、云冈石窟、麦积山石窟并称中国四大石窟．现有一石窟的某处“浮雕像”共7层，每上层的数量是下层的2倍，总共有1016个“浮雕像”，这些“浮雕像”构成一幅优美的图案，若从最下层往上“浮雕像”的数量构成一个数列 ${a_{n}}$ ，则 $l o g_{2} (a_{3} \cdot a_{5})$ 的值为（）

A、8 B、10 C、12 D、16

查看试题解析
8. 已知 $a > \frac{1}{2}$ 且 $2 a = e^{a - \frac{1}{2}}$ ， $b > \frac{1}{3}$ 且 $3 b = e^{b - \frac{1}{3}}$ ， $c > \frac{1}{4}$ 且 $4 c = e^{c - \frac{1}{4}}$ ，则（）

A、 $\frac{l n a}{b c} < \frac{l n b}{a c} < \frac{l n c}{a b}$ B、 $\frac{l n a}{b c} < \frac{l n c}{a b} < \frac{l n b}{a c}$ C、 $\frac{l n c}{a b} < \frac{l n b}{a c} < \frac{l n a}{b c}$ D、 $\frac{l n b}{a c} < \frac{l n a}{b c} < \frac{l n c}{a b}$

查看试题解析

二、多选题

9. 已知数列 ${a_{n}}$ 的通项公式为 $a_{n} = {\begin{array}{l} n ， n = 2 k - 1 ， \\ 2 \times 3^{\frac{n}{2} - 1} ， n = 2 k \end{array} (k \in N^{*})$ ， $S_{n}$ 是数列 ${a_{n}}$ 的前n项和，若 $\exists m \in N^{*}$ ，使 $S_{2 m} = a_{t} S_{2 m - 1} (t \in N^{*})$ ，则 $a_{t} =$ （）

A、1 B、2 C、3 D、4

查看试题解析
10. 已知三次函数 $f (x) = a x^{3} + b x^{2} + c x - 1$ ，若函数 $g (x) = f (- x) + 1$ 的图象关于点（1，0）对称，且 $g (- 2) < 0$ ，则（）

A、 $a < 0$ B、 $g (x)$ 有3个零点 C、 $f (x)$ 的对称中心是 $(- 1 ， 0)$ D、 $12 a - 4 b + c < 0$

查看试题解析
11. 已知球O的半径为4，球心O在大小为60°的二面角 $α - l - β$ 内，二面角 $α - l - β$ 的两个半平面所在的平面分别截球面得两个圆 $O_{1}$ ， $O_{2}$ ，若两圆 $O_{1}$ ， $O_{2}$ 的公共弦AB的长为4，E为AB的中点，四面体 $O A O_{1} O_{2}$ 的体积为V，则正确的是（）

A、O，E， $O_{1}$ ， $O_{2}$ 四点共圆 B、 $O E = 2 \sqrt{3}$ C、 $O_{1} O_{2} = \sqrt{3}$ D、V的最大值为 $\frac{\sqrt{3}}{2}$

查看试题解析
12. 已知抛物线C： $y^{2} = 2 p x$ ( $p$ >0)的焦点F与圆 $E ： x^{2} + y^{2} - 2 x = 0$ 的圆心重合，直线 $l$ 与C交于 $A (x_{1} ， y_{1}) 、 B (x_{2} ， y_{2})$ 两点，且满足： $\vec{O A} \cdot \vec{O B} = 0$ (其中O为坐标原点且A、B均不与O重合)，则（）

A、 $x_{1} x_{2} = 16 ， y_{1} y_{2} = - 16$ B、直线 $l$ 恒过定点 $(4 ， 0)$ C、A、B中点轨迹方程： $y^{2} = 2 x - 4$ D、 $△ A O B$ 面积的最小值为16

查看试题解析

三、填空题

13. 若 ${(1 + 3 x)}^{5} = a_{0} + a_{1} x + a_{2} x^{2} + a_{3} x^{3} + a_{4} x^{4} + a_{5} x^{5}$ ，则 $a_{0} - a_{1} + a_{2} - a_{3} + a_{4} - a_{5}$ 的值为．

查看试题解析
14. 生物入侵是指生物由原生存地侵入到另一个新的环境，从而对入侵地的生态系统造成危害的现象.若某入侵物种的个体平均繁殖数量为 $Q$ ，一年四季均可繁殖，繁殖间隔T为相邻两代间繁殖所需的平均时间.在物种入侵初期，可用对数模型 $K (n) = λ l n n$ （ $λ$ 为常数）来描述该物种累计繁殖数量 $n$ 与入侵时间K（单位：天）之间的对应关系，且 $Q = \frac{T}{λ} + 1$ ，在物种入侵初期，基于现有数据得出 $Q = 6$ ， $T = 50$ .据此估计该物种累计繁殖数量比初始累计繁殖数量增加 $11$ 倍所需要的时间为（ $l n 2 \approx 0.69$ ， $l n 3 \approx 1.10$ ）天.

查看试题解析
15. 英国数学家莫利提出：将三角形各内角三等分，靠近某边的两条三分角线相交于一点，则这样的三个交点构成一个正三角形（如下图所示）.若△ $A B C$ 为等腰直角三角形，且 $A C = 2$ ，则△ $D E F$ 的面积是.

查看试题解析
16. 如图，在四边形 $A B C D$ 中， $∠ B = 60^{°} ， A B = 3$ ， $B C = 6$ ，且 $\vec{A D} = λ \vec{B C} ， \vec{A D} \cdot \vec{A B} = - \frac{3}{2}$ ，则实数 $λ$ 的值为，若 $M ， N$ 是线段 $B C$ 上的动点，且 $| \vec{M N} | = 1$ ，则 $\vec{D M} \cdot \vec{D N}$ 的最小值为．

查看试题解析

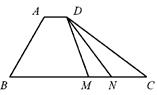
四、解答题

17. 已知数列 ${a_{n}}$ 满足 $a_{1} = 2$ ，前 $n$ 项的和 $S_{n}$ ，且 $a_{n + 1} + a_{n} = 3 \times 2^{n}$ .

(1)、写出 $a_{2} ， a_{3}$ ，并求出数列 ${a_{n}}$ 的通项公式；

(2)、在① $b_{n} = l o g_{2} (a_{n} a_{n + 1} + λ)$ ；② $b_{n} = l o g_{2} (S_{n} + λ)$ 这两个条件中任选一个补充在下面横线中，并加以解答.若数列 ${b_{n}}$ 满足_________，求实数 $λ$ 使得数列 ${b_{n}}$ 是等差数列.
（注：如果求解了两个问题，则按照第一个问题解答给分）

查看试题解析
18. 已知数列 ${a_{n}} ， {b_{n}}$ ，满足 $a_{1} = 1 ， b_{1} = \frac{10}{3} ， b_{n} = \frac{4}{3} a_{n - 1} + b_{n - 1} ， a_{n} = \frac{3}{2} b_{n - 1} ， n \geq 2$ .

(1)、证明 ${a_{n + 1} + a_{n}}$ 是等比数列，并求 ${a_{n}}$ 的通项公式；

(2)、设数列 ${\frac{1}{a_{n}}}$ 的前n项和为 $T_{n}$ ，证明： $T_{n} < \frac{3}{2}$ .

查看试题解析
19. 如图，在三棱锥 $P - A B C$ 中，AB是 $△ A B C$ 外接圆的直径， $△ P A C$ 是边长为2的等边三角形，E，F分别是PC，PB的中点， $P B = A B$ ， $B C = 4$ .

(1)、求证：平面 $P A C ⊥$ 平面ABC；

(2)、求直线AB与平面AEF所成角的正弦值.

查看试题解析
20. 已知椭圆 $E ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左、右焦点分别为 $F_{1}$ ， $F_{2}$ ，离心率 $e = \frac{\sqrt{2}}{2}$ ， P为椭圆上一动点， $△ P F_{1} F_{2}$ 面积的最大值为2.

(1)、求椭圆E的方程；

(2)、若C，D分别是椭圆E长轴的左、右端点，动点M满足 $M D ⊥ C D$ ，连结CM交椭圆于点N，O为坐标原点.证明： $\vec{O M} \cdot \vec{O N}$ 为定值；

(3)、平面内到两定点距离之比是常数 $λ (λ \neq 1)$ 的点的轨迹是圆.椭圆E的短轴上端点为A，点Q在圆 $x^{2} + y^{2} = 8$ 上，求 $2 | Q A | + | Q P | - | P F_{2} |$ 的最小值.

查看试题解析
21. 春节期间，我国高速公路继续执行“节假日高速免费政策” .某路桥公司为了解春节期间车辆出行的高峰情况，在某高速收费点发现大年初三上午9：20~10：40这一时间段内有600辆车通过，将其通过该收费点的时刻绘成频率分布直方图.其中时间段9：20~9：40记作区间 $[20 ， 40)$ ， 9：40~10：00记作 $[40 ， 60)$ ， 10：00~10：20记作 $[60 ， 80)$ ， 10：20~10：40记作 $[80 ， 100]$ ，例如：10点04分，记作时刻64.
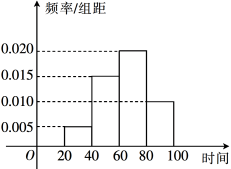
参考数据：若 $T \sim N (μ ， σ^{2})$ ，则 $P (μ - σ < T < μ + σ) = 0.6826$ ， $P (μ - 2 σ < T < μ + 2 σ) = 0.9544$ ， $P (μ - 3 σ < T < μ + 3 σ) = 0.9974$ .

(1)、估计这600辆车在9：20~10：40时间段内通过该收费点的时刻的平均值（同一组中的数据用该组区间的中点值代表）；

(2)、为了对数据进行分析，现采用分层抽样的方法从这600辆车中抽取10辆，再从这10辆车中随机抽取4辆，记X为9：20~10：00之间通过的车辆数，求X的分布列与数学期望；

(3)、由大数据分析可知，车辆在春节期间每天通过该收费点的时刻T服从正态分布 $N (μ ， σ^{2})$ ，其中 $μ$ 可用这600辆车在9：20~10：40之间通过该收费点的时刻的平均值近似代替， $σ^{2}$ 可用样本的方差近似代替（同一组中的数据用该组区间的中点值代表），已知大年初五全天共有1000辆车通过该收费点，估计在9：46~10：40之间通过的车辆数（结果保留到整数）.

查看试题解析
22. 已知函数 $f (x) = \frac{1 - x}{1 + x} l n x$ .

(1)、求 $f (x)$ 的单调区间；

(2)、当 $f (x_{1}) = f (x_{2}) (x_{1} \neq x_{2})$ 时，证明： $x_{1} + x_{2} > 2$ .

查看试题解析