河北省保定市2022届高三下学期数学二模试卷

试卷更新日期：2022-06-15 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知集合 $A = {x | x > 2}$ ， $B = {x | (x - 1) (x - 3) < 3}$ ，则 $A ∪ B =$ （）

A、 ${x | x > 1}$ B、 ${x | 2 < x < 3}$ C、 ${x | x > 0}$ D、 ${x | 2 < x < 4}$

查看试题解析
2. 已知向量 $\vec{A B} = (2 ， - 1)$ ， $\vec{B C} = (1 ， - 3)$ ，则 $| \vec{A C} | =$ （）

A、3 B、4 C、5 D、6

查看试题解析
3. 某研究机构为了了解初中生语文成绩的平均分y（单位：分）与每周课外阅读时间x（单位：分钟）是否存在线性关系，搜集了100组数据（ $\sum_{i = 1} x_{i} = 3000$ ， $\sum_{i = 1} y_{i} = 7900$ ），并据此求得y关于x的线性回归方程为 $y = 0.3 x + a$ .若一位初中生的每周课外阅读时间为2个小时，则可估计她的语文成绩的平均分为（）

A、70.6 B、100 C、106 D、110

查看试题解析
4. 已知 $α 、 β$ 是空间两个不同的平面，则“平面 $α$ 上存在不共线的三点到平面 $β$ 的距离相等”是“ $α / / β$ ”的（）

A、充分非必要条件 B、必要非充分条件 C、充要条件 D、非充分非必要条件

查看试题解析
5. 若函数 $f (\frac{x - 1}{x}) = \frac{1}{x^{2}} - \frac{2}{x} + 1$ ，则函数 $g (x) = f (x) - 4 x$ 的最小值为（）

A、-1 B、-2 C、-3 D、-4

查看试题解析
6. 已知函数 $f (x) = 2 s i n (ω x + \frac{π}{3}) + 1 (ω > 0)$ ， $\forall x \in R$ ， $f (x) ≤ f (\frac{π}{2})$ ，且 $f (x)$ 在 $[0 ， \frac{π}{4}]$ 上单调递增，则 $ω =$ （）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、2 D、3

查看试题解析
7. 已知a， $b \in (0 ， + \infty)$ ，且 $a^{2} + 3 a b + 4 b^{2} = 7$ ，则a+2b的最大值为（）

A、2 B、3 C、 $2 \sqrt{2}$ D、 $3 \sqrt{2}$

查看试题解析
8. 已知双曲线C： $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左､右焦点分别为 $F_{1}$ ， $F_{2}$ ，直线l： $y = k x (k \neq 0)$ 与C交于 $M ， N$ 两点，且四边形 $M F_{1} N F_{2}$ 的面积为 $8 a^{2}$ .若点 $M$ 关于点 $F_{2}$ 的对称点为 $M'$ ，且 $| M' N | = | M N |$ ，则C的离心率是（）

A、 $\sqrt{3}$ B、 $\sqrt{5}$ C、3 D、5

查看试题解析

二、多选题

9. 已知复数z满足方程 $(z^{2} - 4) (z^{2} - 4 z + 5) = 0$ ，则（）

A、z可能为纯虚数 B、方程各根之和为4 C、z可能为 $2 - i$ D、方程各根之积为-20

查看试题解析
10. 已知O为坐标原点，椭圆C： $\frac{x^{2}}{6} + \frac{y^{2}}{2} = 1$ 的左､右焦点分别为 $F_{1}$ ， $F_{2}$ ， $A ， B$ 两点都在 $C$ 上，且 $\vec{A O} = \vec{O B}$ ，则（）

A、 $| A B |$ 的最小值为4 B、 $| A F_{1} | + | B F_{1} |$ 为定值 C、存在点 $A$ ，使得 $A F_{1} ⊥ A F_{2}$ D、C的焦距是短轴长的 $\sqrt{2}$ 倍

查看试题解析
11. 若直线 $y = 3 x + m$ 是曲线 $y = x^{3} (x > 0)$ 与曲线 $y = - x^{2} + n x - 6 (x > 0)$ 的公切线，则（）

A、 $m = - 2$ B、 $m = - 1$ C、 $n = 6$ D、 $n = 7$

查看试题解析
12. 已知函数 $y = 3^{2^{x}} - 2^{3^{x}}$ 在 $(0 ， + ∞)$ 上先增后减，函数 $y = 4^{3^{x}} - 3^{4^{x}}$ 在 $(0 ， + ∞)$ 上先增后减.若 $l o g_{2} (l o g_{3} x_{1}) =$ $l o g_{3} (l o g_{2} x_{1}) = a > 0$ ， $l o g_{2} (l o g_{4} x_{2}) = l o g_{4} (l o g_{2} x_{2}) = b$ ， $l o g_{3} (l o g_{4} x_{3}) = l o g_{4} (l o g_{3} x_{3}) = c > 0$ ，则（）

A、 $a < c$ B、 $b < a$ C、 $c < a$ D、 $a < b$

查看试题解析

三、填空题

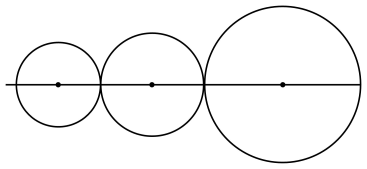
13. 若 $(2 x + \frac{1}{x}) {(x + \frac{1}{x})}^{n}$ 展开式中各项的系数之和为96，则展开式中 $x^{2}$ 的系数为.

查看试题解析
14. 现有10个圆的圆心都在同一条直线上，从左到右它们的半径依次构成首项为1，公比为2的等比数列，从第2个圆开始，每个圆都与前一个圆外切，前3个圆如图所示，若P，Q分别为第1个圆与第10个圆上任意一点，则 $| P Q |$ 的最大值为.（用数字作答）

查看试题解析
15. 在《九章算术》中，将四个面都是直角三角形的三棱锥称为鳖臑.已知在鳖臑P-ABC中，AB⊥BC，PA⊥平面ABC，且 $P A = A B = 2 B C = 4$ ，则鳖臑P-ABC外接球的体积是.

查看试题解析
16. 已知 $8 t a n^{3} θ + 2 t a n θ - \frac{4}{c o s^{2} θ} > - 3$ ，则 $t a n (θ + \frac{7 π}{4})$ 的取值范围为.

查看试题解析

四、解答题

17. 已知公差为2的等差数列 ${a_{n}}$ 的前n项和为 $S_{n}$ ，且 $S_{4} = 16$ .

(1)、求 ${a_{n}}$ 的通项公式.

(2)、若 $b_{n} = \frac{1}{a_{n} a_{n + 2}}$ ，数列 ${b_{n}}$ 的前n项和为 $T_{n}$ ，证明 $T_{n} < \frac{1}{3}$ .

查看试题解析
18. 在△ABC中，角A，B，C的对边分别为a，b，c，且 $s i n^{2} B + s i n^{2} C = (s i n A + 2 s i n B s i n C) s i n A$ .

(1)、求角A；

(2)、若 $a = \sqrt{17}$ ， $b = 3$ ，求△ABC的面积.

查看试题解析
19. 甲､乙两人进行一次乒乓球比赛，比赛最多打5个回合，先胜3回合者胜出且比赛结束.在每回合比赛中，先发球者获胜的概率为0.6，胜者获得下一回合先发球的资格.已知第1回合中，甲先发球.

(1)、求比赛只进行了3回合的概率；

(2)、设比赛共进行了X回合，求X的数学期望.

查看试题解析
20. 如图1，在Rt△ABC中， $A B ⊥ B C$ ， $A C = 2 A B = 12$ ， E，F都在AC上，且 $A E ： E F ： F C = 3 ： 4 ： 5$ ， $E B ∥ F G$ ，将△AEB，△CFG分别沿EB，FG折起，使得点A，C在点P处重合，得到四棱锥P-EFGB，如图2.

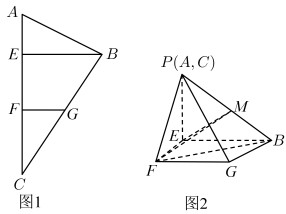(1)、证明： $E F ⊥ P B$ .

(2)、若M为PB的中点，求钝二面角B-FM-E的余弦值.

查看试题解析
21. 已知函数 $f (x) = e^{x - 1} - l n x - x l n a + l n a$ .

(1)、若 $a = 1$ ，证明： $f (x) \geq 1$ .

(2)、当 $x \in [1 ， + ∞)$ 时， $f (x) \geq 1$ 恒成立，求a的取值范围.

查看试题解析
22. 已知抛物线 $Ω ： y^{2} = 4 x$ .

(1)、直线 $l ： y = k (x - 1)$ 与 $Ω$ 交于A、B两点，O为坐标原点.
从下面的①②两个问题中任选一个作答，如果两个都作答，则按所做的第一个计分.
①证明： $| O A | \cdot | O B | = \sqrt{4 | A B | + 9}$ .
②若 $∠ A O B = \frac{2 π}{3}$ ，求 $k^{2}$ 的值；

(2)、已知点 $P (1 ， 2)$ ，直线 $m$ 与 $Ω$ 交于C、D两点（均异于点 $P$ ），且 $k_{P C} + k_{P D} = 1$ .过 $P$ 作直线 $m$ 的垂线，垂足为 $Q$ ，试问是否存在定点 $M$ ，使得 $| Q M |$ 为定值？若存在，求出定值；若不存在，说明理由.

查看试题解析