吉林省长春市南关区2020-2021学年八年级上学期期末数学试题
试卷更新日期:2022-06-15 类型:期末考试
一、单选题
-
1. 4的平方根是( )A、±2 B、2 C、﹣2 D、±2. 在 , ﹣1.6,0,2这四个数中,最大的数是( )A、 B、﹣1.6 C、0 D、23. 下列计算正确的是( )A、(a2)3=a5 B、(2a2)2=2a4 C、a3•a4=a7 D、a4÷a=a44. 某校为丰富学生的课余生活成立了兴趣小组,学生会对全校400名学生各自最喜欢的兴趣小组进行问卷调查后(每人选一种),绘制成如图所示的扇形统计图,选择球类的人数为( )
 A、40人 B、60人 C、80人 D、100人5. 如图,在△ABC中,∠C=90°,点D在边BC上,AD=BD,DE平分∠ADB交AB于点E.若AC=12,BC=16,则AE的长为( )
A、40人 B、60人 C、80人 D、100人5. 如图,在△ABC中,∠C=90°,点D在边BC上,AD=BD,DE平分∠ADB交AB于点E.若AC=12,BC=16,则AE的长为( ) A、6 B、8 C、10 D、126. 如图,在△ABC中,∠C=90°,AC>BC.用直尺和圆规在边AC上确定一点P,使点P到点A、点B的距离相等,则符合要求的作图痕迹是( )A、
A、6 B、8 C、10 D、126. 如图,在△ABC中,∠C=90°,AC>BC.用直尺和圆规在边AC上确定一点P,使点P到点A、点B的距离相等,则符合要求的作图痕迹是( )A、 B、
B、 C、
C、 D、
D、 7. 如图,在△ABC中,AC的垂直平分线交边AC于点D,交边BC于点E,连结AE.若AB=6,BC=9,则△ABE的周长为( )
7. 如图,在△ABC中,AC的垂直平分线交边AC于点D,交边BC于点E,连结AE.若AB=6,BC=9,则△ABE的周长为( ) A、24 B、21 C、18 D、158. 勾股定理是人类最伟大的科学发现之一,在我国古代《周髀算经》中早有记载.如图①,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图②的方式放置在最大正方形内.若图中阴影部分图形的面积为3,则较小两个正方形重叠部分图形的面积为( )
A、24 B、21 C、18 D、158. 勾股定理是人类最伟大的科学发现之一,在我国古代《周髀算经》中早有记载.如图①,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图②的方式放置在最大正方形内.若图中阴影部分图形的面积为3,则较小两个正方形重叠部分图形的面积为( ) A、2 B、3 C、5 D、6
A、2 B、3 C、5 D、6二、填空题
-
9. 的立方根是 .10. 计算:12x5y÷6xy= .11. 分解因式: = .12. 如图,在△ABC中,AB=AC,AD⊥BC于点D.若BC=28,则BD的长为 .
 13. 如图,在△ABC中,D是BC边上一点,且AB=AD=DC,∠BAD=40°,则∠C的度数为 .
13. 如图,在△ABC中,D是BC边上一点,且AB=AD=DC,∠BAD=40°,则∠C的度数为 . 14. 如图,所有四边形都是正方形,所有三角形都是直角三角形,若正方形A、C、D的面积依次为4、6、18,则正方形B的面积为.
14. 如图,所有四边形都是正方形,所有三角形都是直角三角形,若正方形A、C、D的面积依次为4、6、18,则正方形B的面积为.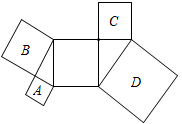
三、解答题
-
15. 计算: .16. 计算: .17. 先化简,再求值: , 其中a= .18. 图①、图②均是6×6的正方形网格,小正方形的边长为1,每个小正方形的顶点称为格点,点A、B均在格点上.只用无刻度的直尺,在给定的网格中按要求画图.

 (1)、在图①中,画一个以AB为底边的等腰三角形ABC,点C在格点上;(2)、在图②中,画一个以AB为腰的等腰三角形ABD,点D在格点上.19. 如图,在△ABC中,AB=AC,D是BC边上的中点,∠B=40°.求:
(1)、在图①中,画一个以AB为底边的等腰三角形ABC,点C在格点上;(2)、在图②中,画一个以AB为腰的等腰三角形ABD,点D在格点上.19. 如图,在△ABC中,AB=AC,D是BC边上的中点,∠B=40°.求: (1)、∠ADC的大小;(2)、∠BAD的大小.20. 图①、图②均是三个角分别为20°,40°,120°的三角形.在图①、图②中,过三角形的一个顶点作直线把此三角形分成两个等腰三角形(图①、图②中的分割线不同).要求画出分割线,并标出等腰三角形底角的度数.
(1)、∠ADC的大小;(2)、∠BAD的大小.20. 图①、图②均是三个角分别为20°,40°,120°的三角形.在图①、图②中,过三角形的一个顶点作直线把此三角形分成两个等腰三角形(图①、图②中的分割线不同).要求画出分割线,并标出等腰三角形底角的度数. 21. 某学校开展了主题为“垃圾分类,绿色生活新时尚”的宣传活动,为了解学生对垃圾分类知识的掌握情况,该校环保社团成员在校园内随机抽取了n名学生进行问卷调查,将他们的得分按优秀、良好、合格、待合格四个等级进行统计,并绘制了不完整的统计表和条形统计图.
21. 某学校开展了主题为“垃圾分类,绿色生活新时尚”的宣传活动,为了解学生对垃圾分类知识的掌握情况,该校环保社团成员在校园内随机抽取了n名学生进行问卷调查,将他们的得分按优秀、良好、合格、待合格四个等级进行统计,并绘制了不完整的统计表和条形统计图.n名学生掌握垃圾分类知识统计表:
等级
频数
频率
优秀
24
0.48
良好
a
0.3
合格
7
b
待合格
4
0.08
根据上面的统计图表回答下列问题:
 (1)、n的值为 , a的值为 , b的值为 .(2)、补全条形统计图;(3)、若全校有1500名学生,请估计该校掌握垃圾分类知识达到“优秀”和“良好”等级的学生共有多少人.22. 如图,在四边形ABCD中,AB=13,BC=5,CD=15,AD=9,对角线AC⊥BC.
(1)、n的值为 , a的值为 , b的值为 .(2)、补全条形统计图;(3)、若全校有1500名学生,请估计该校掌握垃圾分类知识达到“优秀”和“良好”等级的学生共有多少人.22. 如图,在四边形ABCD中,AB=13,BC=5,CD=15,AD=9,对角线AC⊥BC.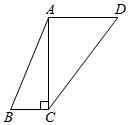 (1)、求AC的长;(2)、求四边形ABCD的面积.23. 已知长方形纸片ABCD,将长方形纸片按如图所示的方式折叠,使点D与点B重合,折痕为EF.
(1)、求AC的长;(2)、求四边形ABCD的面积.23. 已知长方形纸片ABCD,将长方形纸片按如图所示的方式折叠,使点D与点B重合,折痕为EF. (1)、△BEF是等腰三角形吗?若是,请说明理由;(2)、若AB=4,AD=8,求BE的长.24. 如图,在锐角△ABC中,AD⊥BC于点D,点E在AD上,DE=DC,BE=AC,点F为BC的中点,连结EF并延长至点M,使FM=EF,连结CM.
(1)、△BEF是等腰三角形吗?若是,请说明理由;(2)、若AB=4,AD=8,求BE的长.24. 如图,在锐角△ABC中,AD⊥BC于点D,点E在AD上,DE=DC,BE=AC,点F为BC的中点,连结EF并延长至点M,使FM=EF,连结CM. (1)、求证:△BDE≌△ADC;(2)、求证:AC⊥MC;(3)、若AC=m,则点A、点M之间的距离为(用含m的代数式表示).25. 教材呈现:如图是华师版八年级上册数学教材第96页的部分内容.
(1)、求证:△BDE≌△ADC;(2)、求证:AC⊥MC;(3)、若AC=m,则点A、点M之间的距离为(用含m的代数式表示).25. 教材呈现:如图是华师版八年级上册数学教材第96页的部分内容.
请根据教材中的分析,结合图①,写出“角平分线的性质定理”完整的证明过程.

定理应用:
(1)、如图②.在△ABC中,∠C=90°,AD平分∠BAC交BC于点D.若AC=3,BC=4,求CD的长;(2)、如图③.在△ABC中,∠ACB=90°,AD平分∠BAC交BC于点D,点P在AD上,点M在AC上.若AC=6,BC=8,则PC+PM的最小值为 .