吉林省长春市德惠市2020-2021学年八年级上学期期末数学试题
试卷更新日期:2022-06-15 类型:期末考试
一、单选题
-
1. 下列计算中,正确的是( )A、 B、 C、 D、2. 把多项式a²-4a分解因式,结果正确的是( )A、a (a-4) B、(a+2)(a-2) C、a(a+2)( a-2) D、(a-2 ) ²-43. 估计58的立方根的大小在( )A、2与3之间 B、3与4之间 C、4与5之间 D、5与6之间4. 一个班有40名学生,在期末体育考核中,优秀的有18人,在扇形统计图中,代表体育优秀扇形的圆心角是( )A、162° B、144° C、216° D、250°5. 如图,已知∠AOB=30°,P是∠AOB平分线上一点,CP∥OB,交OA于点C,PD⊥OB,垂足为点D,且PC=4,则PD等于( )
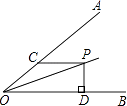 A、1 B、2 C、4 D、86. 如图,在 与 中, , .若 ,则 的度数为( )
A、1 B、2 C、4 D、86. 如图,在 与 中, , .若 ,则 的度数为( ) A、52 ° B、62° C、72° D、118°7. 图①是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中的边长为6的直角边分别向外延长一倍,得到图②所示的“数学风车”,则这个风车的外围周长是( )
A、52 ° B、62° C、72° D、118°7. 图①是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中的边长为6的直角边分别向外延长一倍,得到图②所示的“数学风车”,则这个风车的外围周长是( ) A、51 B、49 C、76 D、无法确定8. 图(1)是一个长为2m,宽为2n(m>n)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是( )
A、51 B、49 C、76 D、无法确定8. 图(1)是一个长为2m,宽为2n(m>n)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是( )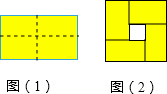 A、2mn B、(m+n)2 C、(m-n)2 D、m2-n2
A、2mn B、(m+n)2 C、(m-n)2 D、m2-n2二、填空题
-
9. 计算: .10. 与数轴上的点一一对应的数是 .11. 定理“等角对等边”改为“如果···,那么···”的是 .12. 代数式 是完全平方式,m= .13. 如图,在 中, ,点 在边 上,且 .若 ,则 的长为 .
 14. 如图,在 与 中,AB、EF相交于点D,点F在边BC上, , , .下列结论:① ;② ;③ 中,正确的是 . (填序号)
14. 如图,在 与 中,AB、EF相交于点D,点F在边BC上, , , .下列结论:① ;② ;③ 中,正确的是 . (填序号)
三、解答题
-
15. 把下列多项式分解因式:(1)、(2)、16. 计算:17. 先化简,再求值: ,其中 .18. 图①、图②均是的正方形网格,每个小正方形的顶点称为格点,的顶点均在格点上,请在图①、图②中各画一个三角形,同时满足以下两个条件:(1)、以点为一个顶点,另外两顶点均在格点上;
 (2)、所作三角形与全等(除外).
(2)、所作三角形与全等(除外). 19. 如图,在 与 中,点 在线段 上,且 , , , .
19. 如图,在 与 中,点 在线段 上,且 , , , . (1)、求证: .(2)、求 的度数.20.
(1)、求证: .(2)、求 的度数.20.在结束了380课时初中阶段数学内容的教学后,唐老师计划安排60课时用于总复习,根据数学内容所占课时比例,绘制如下统计图表(图1~图3),请根据图表提供的信息,回答下列问题:
 (1)、图1中“统计与概率”所在扇形的圆心角为度;(2)、图2、3中的a= , b=;(3)、在60课时的总复习中,唐老师应安排多少课时复习“数与代数”内容?21. 如图,将一张大长方形纸板按图中虚线裁剪成9块,其中有2块是边长为a厘米的大正方形,2块是边长都为b厘米的小正方形,5块是长为a厘米,宽为b厘米的相同的小长方形,且a>b.
(1)、图1中“统计与概率”所在扇形的圆心角为度;(2)、图2、3中的a= , b=;(3)、在60课时的总复习中,唐老师应安排多少课时复习“数与代数”内容?21. 如图,将一张大长方形纸板按图中虚线裁剪成9块,其中有2块是边长为a厘米的大正方形,2块是边长都为b厘米的小正方形,5块是长为a厘米,宽为b厘米的相同的小长方形,且a>b.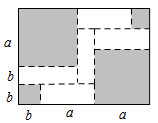 (1)、观察图形,可以发现代数式2a²+5ab+2b²可以因式分解为.(2)、若图中阴影部分的面积为242平方厘米,大长方形纸板的周长为78厘米,求图中空白部分的面积.22. 教材呈现:下图是华师版八年级上册数学教材页的部分内容.
(1)、观察图形,可以发现代数式2a²+5ab+2b²可以因式分解为.(2)、若图中阴影部分的面积为242平方厘米,大长方形纸板的周长为78厘米,求图中空白部分的面积.22. 教材呈现:下图是华师版八年级上册数学教材页的部分内容.
 (1)、请根据教材内容,结合图①,写出完整的解题过程.(2)、拓展:如图②,在图①的的边上取一点 , 连接 , 将沿翻折,使点的对称点落在边上.
(1)、请根据教材内容,结合图①,写出完整的解题过程.(2)、拓展:如图②,在图①的的边上取一点 , 连接 , 将沿翻折,使点的对称点落在边上.①求的长.
②的长 ▲ .
23. 是经过顶点的一条直线, . 、分别是直线上两点,点在点的左侧,且 .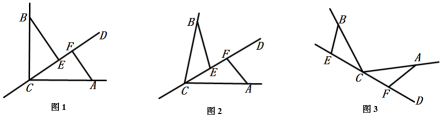 (1)、直线经过的内部,、两点在射线上.
(1)、直线经过的内部,、两点在射线上.①如图1,若 , , 则 ▲ (填“”、“”或“”);、、三条线段之间的数量关系是: ▲ .
②如图2,若 , , ①中的两个结论是否仍然成立,请说明理由.
(2)、如图3,若直线经过的外部, , 请直接写出、、三条线段之间的数量关系.24. 如图,是等边三角形, . 动点分别从点同时出发,动点以的速度沿向终点运动.动点以的速度沿射线运动.当点停止运动时,点也随之停止运动.点出发后,过点作交于点 , 连结 , 以为边作等边三角形 , 连结 , 设点的运动时间为 (1)、用含的代数式表示的长.(2)、求的周长(用含的代数式表示).(3)、求的长(用含的代数式表示).(4)、当的边与垂直时,直接写出的值.
(1)、用含的代数式表示的长.(2)、求的周长(用含的代数式表示).(3)、求的长(用含的代数式表示).(4)、当的边与垂直时,直接写出的值.