吉林省吉林市舒兰市2020-2021学年八年级上学期期末数学试题

试卷更新日期：2022-06-15 类型：期末考试

进入出卷网下载

一、单选题

1. 如图甲骨文中，不是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 下列长度的三条线段能组成三角形的是（）

A、 $3 c m ， 4 c m ， 8 c m$ ． B、 $5 c m ， 6 c m ， 11 c m$ ． C、 $5 c m ， 9 c m ， 6 c m$ ． D、 $6 c m ， 3 c m ， 2 c m$ ．

查看试题解析
3. 下列运算错误的是（）

A、 $(- a)^{2} = a^{2}$ ． B、 $(- 6 a^{2} b) \div (2 a b) = - 3 a$ ． C、 $2^{- 3} = \frac{1}{8}$ ． D、 $(- 1)^{0} = - 1$ ．

查看试题解析
4. 如图，在△ABC中，以点B为圆心，以BA长为半径画弧交边BC于点D，连接AD．若∠B=40°，∠C=36°，则∠DAC的度数是（）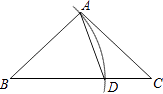

A、70° B、44° C、34° D、24°

查看试题解析
5. 等腰三角形的一个角是80°，则它的一个底角的度数是（）

A、20°或80° B、50° C、80° D、50°或80°

查看试题解析
6. 如图，△ABC的周长为30 cm．把△ABC的边AC对折，使顶点C和点A重合，折痕交BC于D，交AC于E，连接AD，若AE=4 cm，则△ABD的周长为（）

A、22 cm B、20 cm C、18 cm D、16 cm

查看试题解析
7. 如果 $x^{2} + (m - 2) x + 9$ 是个完全平方式，那么 $m$ 的值是（）

A、8 B、-4 C、±8 D、8或-4

查看试题解析
8. 探索：
$(x - 1) (x + 1) = x^{2} - 1$
$(x - 1) (x^{2} + x + 1) = x^{3} - 1$
$(x - 1) (x^{3} + x^{2} + x + 1) = x^{4} - 1$
$(x - 1) (x^{4} + x^{3} + x^{2} + x + 1) = x^{5} - 1$
……
判断2²⁰²⁰+2²⁰¹⁹+2²⁰¹⁸+…+2²+2+1的值的个位数是几？（）

A、1 B、3 C、5 D、7

查看试题解析

二、填空题

9. 人体中红细胞的直径约为 $0.00000792 m$ ，用科学记数法表示这个数应为 $m$ ．

查看试题解析
10. 若分式 $\frac{x^{2} - 1}{5 x - 5}$ 的值为0，则实数 $x$ 的值为．

查看试题解析
11. 分解因式 $2 a^{2} - 4 a b + 2 b^{2} =$ ．

查看试题解析
12. 在平面直角坐标系中，若点 $P (m + 1 ， 3 m + 1)$ 和点 $Q (2 m + 3 ， m + 7)$ 关于 $x$ 轴对称，则 $m$ 的值为．

查看试题解析
13. 一个正多边形的内角和为 $1080 °$ ，则这个正多边形的每个外角的度数为.

查看试题解析
14. 下列各图中，左面ΔABC的边长为a、b、c，则甲、乙、丙三个三角形中和左侧△ABC不全等的是．

查看试题解析
15. 若分式方程 $2 + \frac{1 - k x}{x - 2} = \frac{1}{2 - x}$ 有增根，则 $k =$ ．

查看试题解析
16. 如图，在△ABC中，∠C=90°，AB=12，AD是△ABC的一条角平分线，E为AB的中点，若CD=4，则△AED的面积为．

查看试题解析

三、解答题

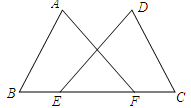
17. 先化简，再求值： $(a + 2)^{2} + (1 + a) (1 - a)$ ，其中 $a = - \frac{3}{2}$ ．

查看试题解析
18. 如图，点E、F在BC上，BE＝CF，AB＝DC，∠B＝∠C．求证：∠A＝∠D．

查看试题解析
19. 解分式方程： $\frac{x}{x - 1} - 1 = \frac{3}{(x - 1) (x + 2)}$

查看试题解析
20. 在平面直角坐标系中，△ABC的三个顶点都在格点上，点A（1，4），点B（-1，0），点C（1，2）．

(1)、请在图中画出与△ABC成轴对称且与△ABC有公共边的格点三角形；(画出一个即可)

(2)、求出你所画图形与△ABC的面积之和．

查看试题解析
21. 先化简 $(1 - \frac{3}{x + 2}) \div \frac{x^{2} - 1}{x + 2}$ ，再从 $1 ， - 1 ， 0 ， - 2$ 中选一个使原式有意义的数代入并求值；

查看试题解析
22. 已知：两个实数 $a ， b$ 满足 $a + b = 2 ， a b = - 1$ ．

(1)、求 $a^{2} - a b + b^{2}$ 的值；

(2)、求 $\frac{b}{a} + \frac{a}{b}$ 的值．

查看试题解析
23. 如图，△ABC中，AB=AC，∠A=36°，AC的垂直平分线交AB于点E，D为垂足，连接EC

(1)、求∠BEC的度数．

(2)、若CE=5，求BC的长．

查看试题解析
24. 如图，在△ABC中，AB＝AC，点D、E、F分别在BC、AB、AC边上，且BE＝CF，AD+EC＝AB．

(1)、△DEF是三角形；当∠A＝40°时，∠DEF的度数为°；

(2)、请你猜想：当∠A为多少度时，∠EDF+∠EFD＝120°，并请说明理由．

查看试题解析
25. 某超市用3000元购进某种干果销售，由于销售状况良好，很快售完．超市又调拨9000元资金购进该种干果，但这次的进价比第一次的进价提高了20%，购进干果的数量是第一次的2倍还多300千克，如果超市此时按每千克9元的价格出售，当大部分干果售出后，余下的100千克按售价的8折售完．

(1)、该种干果的第一次进价是每千克多少元？

(2)、超市第二次销售该种干果盈利了多少元？

查看试题解析
26. 如图，等边△ABC的边长为 $10 c m$ ．点P从点C出发，沿C→B→A→C的方向运动，速度为 $4 c m / s$ ；同时点Q从点B出发，沿B→A→C的方向运动，速度为 $3 c m / s$ ，两个点有一个点到达终点时，另一个点随之停止运动．设运动时间为 $x (s)$ ，解答下列问题：

(1)、当 $2.5 < x < 5$ 时，BP= $c m$ （用含 $x$ 的式子表示）；

(2)、当 $x$ =时，PQ//BC，此时，△APQ是三角形；

(3)、当 $B P = 2 c m$ 时，求 $x$ 的值．

查看试题解析