广东省深圳市南山区2020-2021学年八年级上学期期末数学试题

试卷更新日期：2022-06-15 类型：期末考试

进入出卷网下载

一、单选题

1. 下列四个实数中，无理数是（）

A、0 B、 $\sqrt{2}$ C、 $\frac{2}{7}$ D、 ${}^{3}{\sqrt{8}}$

查看试题解析
2. 点A（3，4）关于x轴的对称点的坐标为（）

A、（3，﹣4） B、（﹣3，﹣4） C、（﹣3，4） D、（﹣4，3）

查看试题解析
3. 某校八（1）班全体同学喜欢的球类运动如图所示．则从图中可以直接看出（　　）

A、喜欢各种球类的具体人数 B、全班同学一学期来喜欢各种球类的变化情况 C、全班的总人数 D、全班同学现在喜欢各种球类人数的百分比

查看试题解析
4. 在平面直角坐标系中，下列说法正确的是（）

A、点P（3，2）到x轴的距离是3 B、若ab＝0，则点P（a，b）表示原点 C、若A（2，﹣2）、B（2，2），则直线AB∥x轴 D、第三象限内点的坐标，横纵坐标同号

查看试题解析
5. 下列命题中，是真命题的是（）

A、相等的角是对顶角 B、两直线平行，同位角相等 C、对应角相等的两个三角形全等 D、如果|a|＝|b|，那么a＝b

查看试题解析
6. 一次函数y＝﹣2x﹣3的图象和性质．叙述正确的是（）

A、y随x的增大而增大 B、与y轴交于点（0，﹣2） C、函数图象不经过第一象限 D、与x轴交于点（﹣3，0）

查看试题解析
7. 下列根式中是最简二次根式的是（）

A、 $\sqrt{\frac{2}{3}}$ B、 $\sqrt{10}$ C、 $\sqrt{9}$ D、 $\sqrt{8}$

查看试题解析
8. 如图的网格中，每个小正方形的边长为1，A，B，C三点均在格点上，结论错误的是（）

A、AB=2 $\sqrt{5}$ B、∠BAC=90° C、 $S_{Δ A B C} = 10$ D、点A到直线BC的距离是2

查看试题解析
9. 某公司用3000元购进两种货物，货物卖出后，一种货物的利润率是10%，另一种货物的利润率是11%，两种货物共获利315元，如果设该公司购进这两种货物所用的费用分别为x元，y元，则列出的方程组是（）

A、 ${\begin{array}{l} x ＋ y ＝ 3000 \\ x (1 ＋ 10 %) ＋ y (1 ＋ 11 %) ＝ 315 \end{array}$ B、 ${\begin{array}{l} x ＋ y ＝ 3000 \\ 10 % x ＋ 11 % y ＝ 315 \end{array}$ C、 ${\begin{array}{l} x ＋ y ＝ 3315 \\ x (1 ＋ 10 %) ＋ y (1 ＋ 11 %) ＝ 315 \end{array}$ D、 ${\begin{array}{l} x ＋ y ＝ 3315 \\ 10 % x ＋ 11 % y ＝ 315 \end{array}$

查看试题解析
10. 勾股定理是人类最伟大的科学发现之一，在我国古算书《周髀算经》中早有记载。如图1，以直角三角形的各边为边分别向外作正方形，再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积，则一定能求出（）

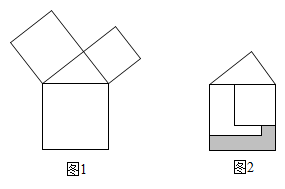A、直角三角形的面积 B、最大正方形的面积 C、较小两个正方形重叠部分的面积 D、最大正方形与直角三角形的面积和

查看试题解析

二、填空题

11. 将直线 $y = - 2 x$ 向上平移1个单位长度，平移后直线的解析式为．

查看试题解析
12. 如图所示，EF⊥AB，∠1＝26°，则当AB∥CD时，∠2＝°.

查看试题解析
13. 如图，已知直线y＝ax+b和直线y＝kx交于点P ，若二元一次方程组 ${\begin{matrix} y = k x \\ y = a x + b \end{matrix}$ 的解为x、y ，则关于x+y＝．

查看试题解析
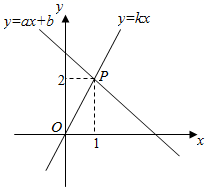14. 下列说法：①无理数就是开方开不尽的数；②满足﹣ $\sqrt{2}$ ＜x＜ $\sqrt{5}$ 的x的整数有4个；③﹣3是 $\sqrt{81}$ 的一个平方根；④不带根号的数都是有理数；⑤不是有限小数的不是有理数；⑥对于任意实数a，都有 $\sqrt{a^{2}}$ ＝a．其中正确的序号是．

查看试题解析
15.
如图，圆柱形玻璃杯高为12cm、底面周长为18cm，在杯内离杯底4cm的点C处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿4cm与蜂蜜相对的点A处，则蚂蚁到达蜂蜜的最短距离为 cm．

查看试题解析

三、解答题

16. 计算题：

(1)、 $\sqrt{27} - \sqrt{12} \times (\sqrt{3} + 1) (\sqrt{3} - 1)$

(2)、3 $\sqrt{18} + \frac{1}{5} \sqrt{50} - 4 \sqrt{\frac{1}{2}}$

(3)、解方程组： ${\begin{array}{l} \frac{x + 1}{3} = 2 y \\ 2 (x + 1) - y = 11 \end{array}$

查看试题解析
17. 为帮助学生了解“预防新型冠状病毒”的有关知识，学校组织了一次线上知识培训，培训结束后进行测试．试题的满分为20分．为了解学生的成绩情况，从七、八年级学生中各随机抽取了20名学生的成绩进行了整理、描述和分析．下面给出了部分信息：
抽取的20名七年级学生成绩是：20，20，20，20，19，19，19，19，18，18，18，18，18，18，18，17，16，16，15，14．
抽取的40名学生成绩统计表
性别
七年级
八年级
平均分
18
18
众数
a
b
中位数
18
c
方差
2.7
2.7
根据以上信息，解答下列问题：

(1)、直接写出表中a，b，c的值：a＝， b＝， c＝．

(2)、在这次测试中，你认为是七年级学生成绩好，还是八年级学生成绩好？请说明理由．

(3)、若九年级随机抽取20名学生的成绩的方差为2.5，则年级成绩更稳定（填“七”或“八”或“九”）．

查看试题解析
18. 如图，小旭放风筝时，风筝线断了，风筝挂在了树上．他想知道风筝距地面的高度．于是他先拉住风筝线垂直到地面上，发现风筝线多出1米，然后把风筝线沿直线向后拉开5米，发现风筝线末端刚好接触地面(如右图为示意图)．请你帮小旭求出风筝距离地面的高度AB．

查看试题解析
19. 如图，在平面直角坐标系中，A（﹣2，0），B（1，4）．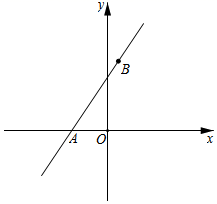

(1)、求直线AB的解析式；

(2)、已知点C在第一象限，且到两坐标轴距离相等，若S_△AOB＝2S_△AOC ，求点C的坐标．

查看试题解析
20. 甲，乙两地相距300千米．一辆货车和一辆轿车先后从甲地出发向乙地，轿车比货车晚出发1.5小时，如图，线段OA表示货车离甲地的距离y（千米）与时间x（小时）之间的函数关系；折线BCD表示轿车离甲地的距离y（千米）与时间x（时）之间的函数关系，线段CD对应的函数解析式是y＝110x﹣195（2.5≤x≤4.5），在轿车行进过程中，轿车行驶多少时间，两车相距15千米？

查看试题解析
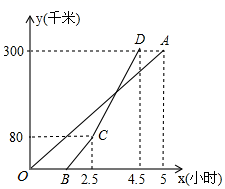21. 某工厂用如图甲所示的长方形和正方形纸板，做成如图乙所示的竖式与横式两种长方体的无盖纸盒．

(1)、现有正方形纸板150张，长方形纸板300张，若这些纸板恰好用完，对可制作横式、竖式两种纸盒各多少个？

(2)、若有正方形纸板30张，长方形纸板a张，做成上述两种纸盒，纸板恰好用完，其中竖式纸盒做了b个，请用含a的代数式表示b．

(3)、在（2）的条件下，当a不超过65张时，最多能做多少个竖式纸盒？

查看试题解析
22. 如图

(1)、如图1，则∠A、∠B、∠C、∠D之间的数量关系为．

(2)、如图2，AP、CP分别平分∠BAD、∠BCD．若∠B＝36°，∠D＝14°，求∠P的度数；

(3)、如图3，CP、AG分别平分∠BCE、∠FAD，AG反向延长线交CP于点P，请猜想∠P、∠B、∠D之间的数量关系．并说明理由．

查看试题解析

性别	七年级	八年级
平均分	18	18
众数	a	b
中位数	18	c
方差	2.7	2.7