广东省梅州市兴宁市2020-2021学年八年级上学期期末数学试题
试卷更新日期:2022-06-15 类型:期末考试
一、单选题
-
1. 下列各数中,是无理数的是( )A、3.14 B、- C、0.57 D、π2. 点所在的象限为( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 如图两平行线、被直线所截,且 , 则的度数为( )
 A、 B、 C、 D、4. 下列各组数中,是勾股数的一组是( )A、4,5,6 B、5,7,2 C、10,24,26 D、12,13,155. 下列根式中与 是同类二次根式的是( )A、 B、 C、 D、6. 如图所示,若 , 则下列结论正确的是( )
A、 B、 C、 D、4. 下列各组数中,是勾股数的一组是( )A、4,5,6 B、5,7,2 C、10,24,26 D、12,13,155. 下列根式中与 是同类二次根式的是( )A、 B、 C、 D、6. 如图所示,若 , 则下列结论正确的是( ) A、 B、 C、 D、7. 如图,已知△ABC中,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )
A、 B、 C、 D、7. 如图,已知△ABC中,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )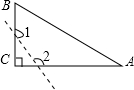 A、90° B、135° C、270° D、315°8. 一蓄水池中有水 , 打开排水阀门开始放水后水池的水量与放水时间有如下关系:
A、90° B、135° C、270° D、315°8. 一蓄水池中有水 , 打开排水阀门开始放水后水池的水量与放水时间有如下关系:放水时间/分
1
2
3
4
…
水池中水量/
48
46
44
42
…
下列说法错误的是( )
A、蓄水池每分钟放水 B、放水18分钟后,水池中水量为 C、蓄水池一共可以放水25分钟 D、放水12分钟后,水池中水量为9. 方程组 的解 , 满足 是 的2倍,则a的值为( )A、-7 B、-11 C、-3 D、-2.210. 一次函数y=kx+k(k<0)的图象大致是( )A、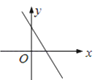 B、
B、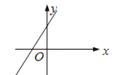 C、
C、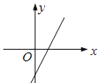 D、
D、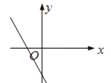
二、填空题
-
11. 日出日落,一天的气温随时间的变化而变化,在这一问题中,自变量是 .12. 在Rt△ABC中,∠C=90°,AB=13,BC=12,则AC= .13. 已知点P在第二象限,且到x轴的距离是3,到y轴的距离是2,则点P的坐标为 .14. 使代数式 有意义的x的取值范围是.15. 若直线经过点(3,2),则k的值是 .16. 如图,直线 , 等边的顶点、分别在直线、上,若边与直线的夹角 , 则边与直线的夹角 .
 17. 求的值,可令 , 则 , 因此 . 仿照以上推理,计算出 .
17. 求的值,可令 , 则 , 因此 . 仿照以上推理,计算出 .三、解答题
-
18. 计算:19. 解方程组:20. 如图,点B、E、C、F在同一条直线上, , , .求证: .
 21. 如图,的顶点分别为 , , .
21. 如图,的顶点分别为 , , . (1)、作出关于轴对称的图形;(2)、写出、、的坐标;(3)、若 , 求的边上的高.22. 为宣传节约用水,小明随机调查了某小区部分家庭5月份的用水情况,并将收集的数据整理成如下统计图.
(1)、作出关于轴对称的图形;(2)、写出、、的坐标;(3)、若 , 求的边上的高.22. 为宣传节约用水,小明随机调查了某小区部分家庭5月份的用水情况,并将收集的数据整理成如下统计图. (1)、小明一共调查了户家庭;(2)、所调查家庭5 月份用水量的众数是; 所调查家庭5 月份用水量的平均数是;(3)、若该小区有400 户居民,请你估计这个小区5 月份的用水量.23. 疫情期间,为保护学生和教师的健康,某学校用33000元购进甲、乙两种医用口罩共计1000盒,甲,乙两种口罩的售价分别是30元/盒,35元/盒.(1)、求甲、乙两种口罩各购进了多少盒?(2)、现已知甲,乙两种口罩的数量分别是20个/盒,25个/盒,按照教育局要求,学校必须储备足够使用十天的口罩,该校师生共计800人,每人每天2个口罩,问购买的口罩数量是否能满足教育局的要求?
(1)、小明一共调查了户家庭;(2)、所调查家庭5 月份用水量的众数是; 所调查家庭5 月份用水量的平均数是;(3)、若该小区有400 户居民,请你估计这个小区5 月份的用水量.23. 疫情期间,为保护学生和教师的健康,某学校用33000元购进甲、乙两种医用口罩共计1000盒,甲,乙两种口罩的售价分别是30元/盒,35元/盒.(1)、求甲、乙两种口罩各购进了多少盒?(2)、现已知甲,乙两种口罩的数量分别是20个/盒,25个/盒,按照教育局要求,学校必须储备足够使用十天的口罩,该校师生共计800人,每人每天2个口罩,问购买的口罩数量是否能满足教育局的要求?

