广东省茂名市化州市2020-2021学年八年级上学期期末数学试题

试卷更新日期：2022-06-15 类型：期末考试

进入出卷网下载

一、单选题

1. 下列几组数能作为直角三角形三边长的是（）

A、3，4，6 B、1，1， $\sqrt{3}$ C、5，12，14 D、 $\sqrt{5}$ ， 2 $\sqrt{5}$ ， 5

查看试题解析
2. 下列各式中，运算正确的是（）

A、 $\sqrt{16} = \pm 4$ B、 $\sqrt{6} \div \sqrt{3} = \sqrt{2}$ C、 $\sqrt{{(- 4)}^{2}} = - 4$ D、 $2 \sqrt{2} + 3 \sqrt{3} = 5 \sqrt{5}$

查看试题解析
3. 某商场对上周末某品牌运动服的销售情况进行了统计，如下表所示：经理决定本周进货时多进一些红色的，可用来解释这一现象的统计知识是（）
颜色
黄色
绿色
白色
紫色
红色
数量（件）
120
150
230
75
430

A、平均数 B、中位数 C、众数 D、平均数与中位数

查看试题解析
4. 方程2x+y=5与下列方程构成的方程组的解为 ${\begin{matrix} x = 3 \\ y = - 1 \end{matrix}$ 的是（）

A、x﹣y=4 B、x+y=4 C、3x﹣y=8 D、x+2y=﹣1

查看试题解析
5. 如图，△ABC中∠ACB＝90°，且CD∥AB．∠B＝60°，则∠1等于（）

A、30° B、40° C、50° D、60°

查看试题解析
6. 若y轴上的点P到x轴的距离为3，则点P的坐标是（）

A、（3，0） B、（0，3） C、（3，0）或（﹣3，0） D、（0，3）或（0，﹣3）

查看试题解析
7. 如图，在四边形ABCD中，连结BD，判定正确的是（）

A、若∠1＝∠2，则AB∥CD B、若∠3＝∠4，则AD∥BC C、若∠A+∠ABC＝180°，则AD∥BC D、若∠C＝∠A，则AB∥CD

查看试题解析
8. 已知函数y=（m+1） $x^{m^{2} - 3}$ 是正比例函数，且图象在第二、四象限内，则m的值是（）

A、2 B、﹣2 C、±2 D、 $\frac{1}{2}$

查看试题解析
9. 一次函数y＝﹣bx﹣k的图象如下，则y＝﹣kx﹣b的图象大致位置是（）

A、 B、 C、 D、

查看试题解析
10. 一根竹竿插到水池中离岸边1.5m远的水底，竹竿高出水面0.5m，若把竹竿的顶端拉向岸边，则竿顶刚好接触到岸边，并且和水面一样高，问水池的深度为（）

A、2m B、2.5cm C、2.25m D、3m

查看试题解析

二、填空题

11. 化简 $\sqrt{4^{2}}$ 的结果是．

查看试题解析
12. 已知数据：﹣1，4，2，﹣2，x的众数是2，那么这组数据的平均数为 .

查看试题解析
13. 点 $(a ， b)$ 在直线 $y = - 2 x + 3$ 上，则 $4 a + 2 b - 1 =$ ．

查看试题解析
14. 平面直角坐标系上有点A（﹣3，4），则它到坐标原点的距离为．

查看试题解析
15. 如图，在直角坐标系中有两条直线，l₁：y＝x+1和L₂：y＝ax+b，这两条直线交于轴上的点（0，1）那么方程组 ${\begin{array}{l} y = x + 1 \\ y = a x + b \end{array}$ 的解是．

查看试题解析
16. 一次函数y＝﹣2x﹣1的图象与x轴、y轴分别交于点A、B，则△AOB的面积是．

查看试题解析
17. 如图，在△ABC中，∠A＝60°，若剪去∠A得到四边形BCDE，则∠1＋∠2＝.

查看试题解析

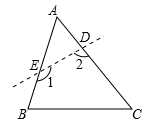
三、解答题

18. 计算： $\frac{\sqrt{18} - \sqrt{10}}{\sqrt{2}}$ + $\sqrt{5}$

查看试题解析
19. 解方程组： ${\begin{array}{l} x + y = 1 \\ 3 x - y = 7 \end{array}$

查看试题解析
20. 某中学八（1）班小明在综合实践课上剪了一个四边形ABCD，如图，连接AC，经测量AB＝12，BC＝9，CD＝8，AD＝17，∠B＝90°．求证：△ACD是直角三角形．

查看试题解析
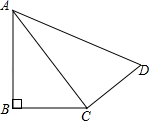21. 已知：如图，在△ABC中，CD⊥AB于点D，E是AC上一点且∠1+∠2＝90°.求证：DE∥BC.

查看试题解析
22. 2018年9月14日至15日，“一带一路”国际合作高峰论坛在北京举行，本届论坛期间，中国同30多个国家签署经贸合作协议，某厂准备生产甲、乙两种商品共8万件销往“一带一路”沿线国家和地区，已知2件甲种商品与3件乙种商品的销售收入相同，3件甲种商品比2件乙种商品的销售收入多1500元．甲种商品与乙种商品的销售单价各多少元？

查看试题解析
23. 在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点的三角形）ABC的顶点A，C的坐标分别为（-4，5），（-1，3）.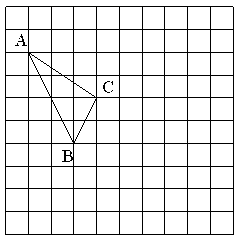

⑴请在如图所示的网格平面内作出平面直角坐标系；
⑵请作出△ABC关于y轴对称的△A′B′C′；
⑶写出点B′的坐标.

查看试题解析

24. 甲、乙、丙三位运动员在相同条件下各射靶10次，每次射靶的成绩如下：

甲：9，10，8，5，7，8，10，8，8，7；

乙：5，7，8，7，8，9，7，9，10，10；

丙：7，6，8，5，4，7，6，3，9，5．

(1)、根据以上数据完成下表：

	平均数	中位数	方差
甲	8	8
乙	8	8	2.2
丙	6		3

(2)、依据表中数据分析，哪位运动员的成绩最稳定，并简要说明理由．

查看试题解析

25. 如图，直线l₁：y＝x+1与直线l₂：y＝mx+n交于点P（1，b），直线l₂与x轴交于点A（4，0）．

(1)、求b的值；

(2)、解关于x，y的方程组 ${\begin{array}{l} y = x + 1 \\ y = m x + n \end{array}$ ，并直接写出它的解；

(3)、判断直线l₃：y＝nx+m是否也经过点P？请说明理由．

查看试题解析

颜色	黄色	绿色	白色	紫色	红色
数量（件）	120	150	230	75	430