广东省茂名市电白区2020-2021学年八年级上学期期末数学试题
试卷更新日期:2022-06-15 类型:期末考试
一、单选题
-
1. 下列实数中,是无理数的为( )A、3.14 B、 C、 D、2. 下列各式中,运算正确的是( )A、 B、 C、 D、3. 下列命题中,是假命题的是( )A、两点之间,线段最短 B、对顶角相等 C、直角的补角仍然是直角 D、同旁内角互补4. 如图,圆柱的底面半径是4,高是5,一只在A点的蚂蚁想吃到B点的食物,需要爬行的最短路径是(π取3)( )
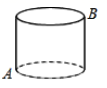 A、9 B、13 C、14 D、255. 一次函数y=kx+b的图象如图所示,则以k、b为坐标的点(k,b)在( )
A、9 B、13 C、14 D、255. 一次函数y=kx+b的图象如图所示,则以k、b为坐标的点(k,b)在( ) A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 一组数据1,4,5,2,8,它们的数据分析正确的是( )A、平均数是5 B、中位数是4 C、方差是30 D、极差是67. 如图,在△ABC中,∠C=36°,将△ABC沿着直线l折叠,点C落在点D的位置,则∠1﹣∠2的度数是( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 一组数据1,4,5,2,8,它们的数据分析正确的是( )A、平均数是5 B、中位数是4 C、方差是30 D、极差是67. 如图,在△ABC中,∠C=36°,将△ABC沿着直线l折叠,点C落在点D的位置,则∠1﹣∠2的度数是( ) A、36° B、72° C、50° D、46°8. 已知 ,则x+y的值为( )A、0 B、﹣1 C、1 D、59. 甲、乙两人在笔直的人行道上同起点、同终点、同方向匀速步行1800米,先到终点的人原地休息.已知甲先出发3分钟,在整个步行过程中,甲、乙两人间的距离(米与甲出发后步行的时间(分之间的关系如图所示,下列结论:①甲步行的速度为60米分;②乙走完全程用了22.5分钟;③乙用9分钟追上甲;④乙到达终点时,甲离终点还有270米.其中正确的结论有 )
A、36° B、72° C、50° D、46°8. 已知 ,则x+y的值为( )A、0 B、﹣1 C、1 D、59. 甲、乙两人在笔直的人行道上同起点、同终点、同方向匀速步行1800米,先到终点的人原地休息.已知甲先出发3分钟,在整个步行过程中,甲、乙两人间的距离(米与甲出发后步行的时间(分之间的关系如图所示,下列结论:①甲步行的速度为60米分;②乙走完全程用了22.5分钟;③乙用9分钟追上甲;④乙到达终点时,甲离终点还有270米.其中正确的结论有 ) A、1个 B、2个 C、3个 D、4个10. 如图,在平面直角坐标系中, , , , …都是等边三角形,其边长依次为2,4,6,…,其中点的坐标为 , 点的坐标为 , 点的坐标为 , 点的坐标为 , …,按此规律排下去,则点的坐标为( )
A、1个 B、2个 C、3个 D、4个10. 如图,在平面直角坐标系中, , , , …都是等边三角形,其边长依次为2,4,6,…,其中点的坐标为 , 点的坐标为 , 点的坐标为 , 点的坐标为 , …,按此规律排下去,则点的坐标为( )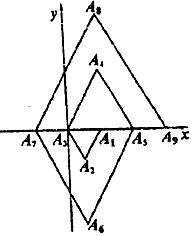 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
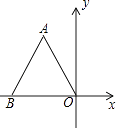
11. 8的平方根是12. 某地教育局拟招聘一批数学教师,现有一名应聘者笔试成绩88分、面试成绩90分,综合成绩按照笔试占45%、面试占55%进行计算,该应聘者的综合成绩为分.13. 如图,边长为4的等边△AOB在平面直角坐标系中的位置如图所示,则点A的坐标为 .
 14. 如图,直线 ,以直线 上的点A为圆心,适当长为半径在右侧画弧,分别交 , 于点 .连结 , .若 ,则 的度数是 .
14. 如图,直线 ,以直线 上的点A为圆心,适当长为半径在右侧画弧,分别交 , 于点 .连结 , .若 ,则 的度数是 .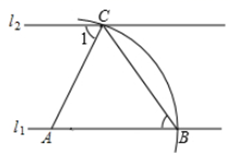 15. 《九章算术》有个题目,大意是:“五只雀、六只燕,共重16两,雀重燕轻,互换其中一只,恰好一样重.”设每只雀、燕的重量分别为x两,y两,可得方程组是 .16. 若以二元一次方程 的解为坐标的点(x,y) 都在直线 上,则常数b=.17. 如图,将直线沿y轴向下平移后的直线恰好经过点 , 且与y轴交于点B,在x轴上存在一点P使得的值最小,则点P的坐标为 .
15. 《九章算术》有个题目,大意是:“五只雀、六只燕,共重16两,雀重燕轻,互换其中一只,恰好一样重.”设每只雀、燕的重量分别为x两,y两,可得方程组是 .16. 若以二元一次方程 的解为坐标的点(x,y) 都在直线 上,则常数b=.17. 如图,将直线沿y轴向下平移后的直线恰好经过点 , 且与y轴交于点B,在x轴上存在一点P使得的值最小,则点P的坐标为 .
三、解答题
-
18. 计算题: .19. 解方程组:20. 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).
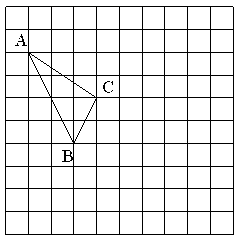
⑴请在如图所示的网格平面内作出平面直角坐标系;
⑵请作出△ABC关于y轴对称的△A′B′C′;
⑶写出点B′的坐标.21. 随着智能手机的普及,微信抢红包已成为春节期间人们最喜欢的活动之一,某校七年级(1)班班长对全班50名学生在春节期间所抢的红包金额进行统计,并绘制成了统计图.请根据以上信息回答:
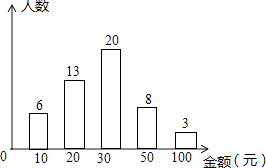 (1)、该班同学所抢红包金额的众数是 , 中位数是;
(1)、该班同学所抢红包金额的众数是 , 中位数是;
(2)、该班同学所抢红包的平均金额是多少元?
(3)、若该校共有18个班级,平均每班50人,请你估计该校学生春节期间所抢的红包总金额为多少元?
22. 为了拉动内需,全国各地汽车购置税补贴活动在2009年正式开始,某经销商在政策出台前一个月共售出某品牌汽车的手动型和自动型共960台,政策出台后的第一个月售出这两种型号的汽车共1228台,其中手动型和自动型汽车的销售量分别比政策出台前一个月增长30%和25%.(1)、在政策出台前一个月,销售的手动型和自动型汽车分别为多少台;(2)、若手动型汽车每台价格为8万元,自动型汽车每台价格为9万元.根据汽车补贴政策,政府按每台汽车价格的5%给购买汽车的用户补贴,问政策出台后的第一个月,政府对这1228台汽车用户共补贴了多少万元.23. 在△ABC中,AD平分∠BAC交BC于点D,在AB上取一点E,使得EA=ED. (1)、求证:DE∥AC;(2)、若ED=EB,BD=2,EA=3,求AD的长.24. 甲、乙两车先后从“深圳书城”出发,沿相同的路线到距书城240km的某市.因路况原因,甲车行驶的路程y (km)与甲车行驶的时间x (h)的函数关系图象为折线 O-A-B, 乙车行驶的路程y (km)与甲车行驶的时间x(h)的函数关系图象为线段CD.
(1)、求证:DE∥AC;(2)、若ED=EB,BD=2,EA=3,求AD的长.24. 甲、乙两车先后从“深圳书城”出发,沿相同的路线到距书城240km的某市.因路况原因,甲车行驶的路程y (km)与甲车行驶的时间x (h)的函数关系图象为折线 O-A-B, 乙车行驶的路程y (km)与甲车行驶的时间x(h)的函数关系图象为线段CD. (1)、求线段AB所在直线的函数表达式;(2)、①乙车比甲车晚出发 ▲ 小时;
(1)、求线段AB所在直线的函数表达式;(2)、①乙车比甲车晚出发 ▲ 小时;②乙车出发多少小时后追上甲车?
(3)、乙车出发多少小时后甲、乙两车相距10千米?25. 如图,在平面直角坐标系中,直线y=−2x+12与x轴交于点A,与y轴交于点B,与直线y=x交于点C. (1)、求点C的坐标.(2)、若P是x轴上的一个动点,直接写出当△POC是等腰三角形时P的坐标.(3)、在直线AB上是否存在点M,使得△MOC的面积是△AOC面积的2倍?若存在,请求出点M的坐标;若不存在,请说明理由.
(1)、求点C的坐标.(2)、若P是x轴上的一个动点,直接写出当△POC是等腰三角形时P的坐标.(3)、在直线AB上是否存在点M,使得△MOC的面积是△AOC面积的2倍?若存在,请求出点M的坐标;若不存在,请说明理由.