广东省江门市台山市2020-2021学年八年级上学期期末数学试题

试卷更新日期：2022-06-15 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各组线段中，能组成三角形的是（）

A、2，3，5 B、3，4，8 C、3，3，4 D、7，4，2

查看试题解析
2. 在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 已知 $x^{2} - 8 x + a$ 可以写成一个完全平方式，则 $a$ 可为（）

A、4 B、8 C、16 D、 $- 16$

查看试题解析
4. 已知 $\frac{3 x - 4}{(x - 1) (x - 2)} = \frac{A}{x - 1} + \frac{B}{x - 2}$ ，则A，B的值分别为（）

A、A＝3，B＝﹣4 B、A＝4，B＝﹣3 C、A＝1，B＝2 D、A＝2，B＝1

查看试题解析
5. 如图，在△ABC中，∠C=90°，∠ABC=60°，BD平分∠ABC，若AD=6，则CD等于（　　）

A、3 B、4 C、5 D、6

查看试题解析
6. 若x+m与x+2的乘积化简后的结果中不含x的一次项，则m的值为（）

A、2 B、-2 C、4 D、-4

查看试题解析
7. 如图，P是∠AOB的平分线上的一点，PC⊥OA，PD⊥OB，垂足分别为C，D．下列结论不一定成立的是（）

A、∠AOP=∠BOP B、PC=PD C、∠OPC=∠OPD D、OP=PC+PD

查看试题解析
8. 一个正方形的边长增加3cm，它的面积就增加99cm² ，这个正方形的边长为（）

A、14cm B、15cm C、16cm D、17cm

查看试题解析
9. 如图所示，正方形网格中，网格线的交点称为格点，已知点A，B是两个格点，如果点C也是图中的格点，且使得△ABC为等腰直角三角形，那么点C的个数为（）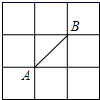

A、4 B、5 C、6 D、7

查看试题解析
10. 如图，在△ABC中，∠C=90°，∠B=30°，以A为圆心，任意长为半径画弧分别交AB，AC于点M和N，再分别以M，N为圆心，大于 $\frac{1}{2}$ MN的长为半径画弧，两弧交于点P，连结AP并延长交BC于点D，则下列说法中正确的个数是（）
①AD是∠BAC的平分线；②∠ADC=60°；③点D在AB的中垂线上；④S_△_DAC：S_△_ABC=1：3．

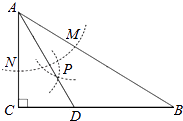A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 用科学记数法表示下数：0.00123= ．

查看试题解析
12. 正六边形的每个内角等于°．

查看试题解析
13. 若 $x^{2} + m x + 16 = {(x + n)}^{2}$ ，则常数 $m =$ .

查看试题解析
14. ${(- \frac{2}{3})}^{2020} \times (1.5)^{2021} =$ ．

查看试题解析
15. 一副分别含有30°和45°角的两个直角三角板，拼成如下图形，则∠1= 度．

查看试题解析
16. 分式方程 $\frac{x^{2} - 25}{x^{2} - 10 x + 25} = 0$ 的解是．

查看试题解析
17. 如图，在△ABC中，AB=AC，∠BAC=30°，D为BC上任意一点，过点D作DE⊥AB，DF⊥AC，垂足分别为E，F，且DE+DF = $\frac{7}{3}$ ，连接AD，则AB=.

查看试题解析

三、解答题

18. 计算：

(1)、 $(- 2 a^{2}) \cdot (- 3 a^{2} b - 4 a b^{2})$

(2)、 $(8 x^{3} - 4 x^{2} + 2 x) \div (- 2 x)$

(3)、 $\frac{x + 3}{x + 2} + \frac{2 - x}{x^{2} - 4}$

查看试题解析
19. 如图，AC＝BC，AE⊥CD于点A，BD⊥CE于点B．

(1)、求证：CD＝CE；

(2)、若点A为CD的中点，求∠C的度数．

查看试题解析
20. 如图，四边形ABCD中，∠B=∠C=90°，E是BC的中点，DE平分∠ADC．

(1)、求证：AE平分∠BAD．

(2)、求证：AD＝AB＋CD．

查看试题解析
21. 先化简，再求值： $\frac{x - 3}{x^{2} - 4} \cdot \frac{x^{2} + 4 x + 4}{x - 3} - (\frac{1}{x - 2} + 2)$ ，其中 $x = - \frac{6}{5}$ ．

查看试题解析
22. 珠海到韶关的距离约为360千米，小刘驾驶小轿车，小张驾驶大货车，两人都从珠海去韶关，小刘比小张晚出发90分钟，最后两车同时到达韶关，已知小轿车的速度是大货车速度的1.5倍.

(1)、分别求小轿车和大货车的速度；

(2)、当小刘行驶了2小时，此时两车相距多少千米?

查看试题解析
23.
如图，△ABC中，AB=AC，AD⊥BC，CE⊥AB，AE=CE．
求证：

(1)、△AEF≌△CEB；

(2)、AF=2CD．

查看试题解析
24. 阅读下列材料：
材料1、将一个形如x²+px+q的二次三项式因式分解时，如果能满足q＝mn且p＝m+n，则可以把x²+px+q因式分解成（x+m）（x+n）.
x²+4x+3＝（x+1）（x+3）（2）x²﹣4x﹣12＝（x﹣6）（x+2）

材料2、因式分解：（x+y）²+2（x+y）+1

解：将“x+y”看成一个整体，令x+y＝A，则原式＝A²+2A+1＝（A+1）²

再将“A”还原，得：原式＝（x+y+1）²

上述解题用到“整体思想”，整体思想是数学解题中常见的一种思想方法，请你解答下列问题：

(1)、根据材料1，把x²﹣6x+8分解因式．

(2)、结合材料1和材料2，完成下面小题：
①分解因式：（x﹣y）²+4（x﹣y）+3；
②分解因式：m（m+2）（m²+2m﹣2）﹣3．

查看试题解析
25. 如图，点O是等边△ABC内一点， $∠ AOB = 110 °$ ， $∠ BOC = α$ ，△BOC≌△ADC，连接OD．

(1)、求证：△COD是等边三角形；

(2)、当 $α = 150 °$ 时，试判断△AOD的形状，并说明理由；

(3)、当△AOD是等腰三角形时，求 $α$ 的度数.

查看试题解析