广东省江门恩平市2020-2021学年八年级上学期期末数学试题

试卷更新日期：2022-06-15 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图案中是轴对称图形的有 $($ $)$

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 下列计算正确的是 $($ $)$

A、 $(a - b)^{2} = a^{2} - b^{2}$ B、 $(x^{2})^{3} = x^{5}$ C、 $x^{8} \div x^{2} = x^{4}$ D、 $x^{2} \cdot x^{5} = x^{7}$

查看试题解析
3. 如图，一扇窗户打开后，用窗钩AB可将其固定，这里所运用的几何原理是（）

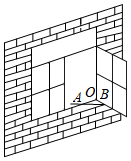A、两点确定一条直线 B、两点之间线段最短 C、三角形的稳定性 D、垂线段最短

查看试题解析
4. 如图，已知E，B，F，C四点在一条直线上， $EB = CF$ ， $∠ A = ∠ D$ ，添加以下条件之一，仍不能证明 $△ ABC$ ≌ $△ DEF$ 的是 $($ $)$

A、 $∠ E = ∠ ABC$ B、 $AB = DE$ C、 $AB / / DE$ D、 $DF / / AC$

查看试题解析
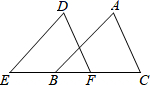5. 下列多项式中能用平方差公式分解因式的是（）

A、 $a^{2}$ + ${(- b)}^{2}$ B、 $5 m^{2} - 20 mn$ C、 $- x^{2} - y^{2}$ D、 $- x^{2} + 9$

查看试题解析
6. 一个多边形的内角和是外角和的2倍，则这个多边形的边数为( )

A、4 B、5 C、6 D、7

查看试题解析
7. 如图，△ABC 中，D、E 分别是 BC、AD 的中点，若△ABC 的面积是 18，则△ABE的面积是（）

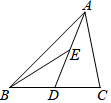A、9 B、4.5 C、6 D、4

查看试题解析
8. 等腰三角形的周长是18 ，其中一边的长为4 ，则其它两边的长分别为（）

A、4 ，10 B、7 ，7 C、4 ，10 或7 ，7 D、无法确定

查看试题解析
9. 如图，DE是△ABC中AC边的垂直平分线，若BC=6cm，AB=8cm，则△EBC的周长是（）

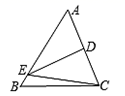A、14cm B、18cm C、20cm D、22cm

查看试题解析
10. 一件工作，甲独做x小时完成，乙独做y小时完成，那么甲、乙合做全部工作需 $($ $)$ 小时

A、 $\frac{1}{x + y}$ B、 $\frac{1}{x} + \frac{1}{y}$ C、 $\frac{1}{x - y}$ D、 $\frac{x y}{x + y}$

查看试题解析

二、填空题

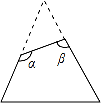
11. 一根头发的直径约为 $0.0000715$ 米，该数用科学记数法表示为．

查看试题解析
12. 已知点 $A (m ， - 3)$ 与点 $B (- 4 ， n)$ 关于x轴对称，则 $m + n$ 的值为．

查看试题解析
13. 已知单项式﹣2x^a+2by^a^﹣b与3x⁴y是同类项，则2a+b的值为.

查看试题解析
14. $R t △ A B C$ 中，CD是斜边AB上的高， $∠ B = 3 0^{∘}$ ， $A D = 2 c m$ ，则BD的长度是．

查看试题解析
15. 如图，一个等边三角形纸片，剪去一个角后得到一个四边形，则图中∠α+∠β= ．

查看试题解析
16. 若 $a + b = 7$ ， $a b = 12$ ，则 $\frac{a^{2} + b^{2}}{a b}$ 的值为．

查看试题解析
17. 如图， $△ A B C$ 中， $∠ A C B = 90 °$ ， $∠ B = 50 °$ ，将 $△ A B C$ 绕点 $C$ 按顺时针方向旋转后得到 $△ A^{'} B^{'} C$ ，点 $B^{'}$ 恰好落在线段AB上， $A C$ 、 $A^{'} B^{'}$ 相交于 $O$ ，则 $∠ C O A^{'}$ 的度数为．

查看试题解析

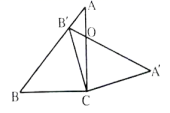
三、解答题

18. 分解因式： $- 2 a^{3} + 12 a^{2} - 18 a$

查看试题解析
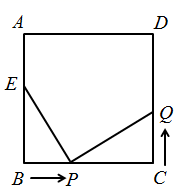
19. 计算： $(1 - \frac{1}{1 - x}) \div \frac{x}{x^{2} - 1}$ ．

查看试题解析
20. 如图所示，在所给正方形网格图中完成下列各题：（保留画图痕迹）
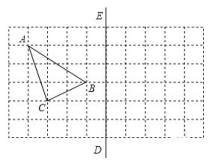
⑴画出格点 $Δ A B C$ 关于直线DE对称的 $Δ A_{1} B_{1} C_{1}$ ；
⑵在DE上取一点 $Q$ ，使 $Δ Q A B$ 的周长最小.

查看试题解析
21. 先化简，再求值： $(x + 2 y) (x - 2 y) + (20 x y^{3} - 8 x^{2} y^{2}) \div 4 x y$ ，其中 $x = 2020$ ， $y = 2021$ ．

查看试题解析
22. 如图，上午8时，一艘轮船从A处出发以每小时20海里的速度向正北航行，10时到达B处，则轮船在A处测得灯塔C在北偏西36°，航行到B处时，又测得灯塔C在北偏西72°，求从B到灯塔C的距离.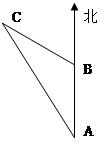

查看试题解析
23. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ，点D、E分别在AB，AC上，CE=BC，连接CD，将线段CD绕点C按顺时针方向旋转 $90 °$ 后得CF，连接EF．

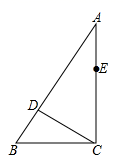(1)、补充完成图形；

(2)、若 $E F / / C D$ ，求证： $∠ B D C = 90 °$ ．

查看试题解析
24. 因课外活动的需要，鹏胜同学第一次在文具店买若干支笔芯，花了30元，第二次再去买该款笔芯时，发现每一盒 $(20$ 支装 $)$ 价钱升了2元，他这一次买该款笔芯的数量是第一次的2倍，花了68元，求他两次买的笔芯分别是多少支？

查看试题解析
25. 如图，在正方形ABCD中， $A B = B C = C D = A D = 10 c m$ ， $∠ A = ∠ B = ∠ C = ∠ D = 90 °$ ，点E在边AB上，且 $A E = 4 c m$ ，如果点 $P$ 在线段BC上以 $2 c m /$ 秒的速度 $B$ 点向 $C$ 点运动，同时，点Q在线段CD上由 $C$ 点向D点运动，设运动时间为t秒．

(1)、若点 $Q$ 与点 $P$ 的运动速度相等，经过2秒后， $△ B P E$ 与 $△ C Q P$ 是否全等？请说明理由；

(2)、若点 $Q$ 与点 $P$ 的运动速度不相等，则当 $t$ 为何值时， $△ B P E$ 与 $△ C Q P$ 全等？此时点 $Q$ 的运动速度为多少？

查看试题解析