广东省广州市天河区2020-2021学年八年级上学期期末数学试题
试卷更新日期：2022-06-15 类型：期末考试
一、单选题
-
1. 下面四个图形分别是节能、节水、低碳和绿色食品标志，在这四个标志中，是轴对称图形的是（ ）A、
B、
C、
D、
2. 在下列长度的三条线段中，能围成三角形的是（ ）A、2，3，4 B、2，3，5 C、3，5，9 D、8，4，43. 如果一个多边形的内角和等于720°，则它的边数为（ ）A、3 B、4 C、5 D、64. 下列运算中正确的是（ ）A、2a3﹣a3＝2 B、2a3•a4＝2a7 C、（2a3）2＝4a5 D、a8÷a2＝a45. 在△ABC中，∠C＝90°，∠A＝60°，AC＝2．则AB的长为（ ）A、1 B、2 C、3 D、46. 分式的值为0，则y的值是（ ）A、5 B、 C、﹣5 D、07. 若x2+kx+16能写成一个多项式的平方形式，则k的值为（ ）A、±8 B、8 C、±4 D、48. 如图，AE∥DF，AE＝DF．添加下列的一个选项后．仍然不能证明△ACE≌△DBF的是（ ）
A、AB＝CD B、EC＝BF C、∠E＝∠F D、EC∥BF9. 如图，在 中， 的垂直平分线交 于点D， 平分 ，若 ，则 的度数为（ ）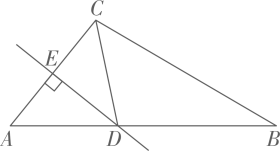
A、 B、 C、 D、10. 如图，△ABC和△ADE是等腰直角三角形，且∠BAC＝∠DAE＝90°，BD，CE交于点F，连接AF．则下列结论错误的是（ ）
A、BD＝CE B、BD⊥CE C、AF平分∠CAD D、∠AFE＝45°二、填空题
-
11. 已知点P的坐标为（﹣2，3）．则它关于y轴对称的点P'的坐标是 ．12. 已知x+y＝6，xy＝7，则x2y+xy2的值是.13. 如图，已知△ABC≌△DEF，∠B＝57°，∠D＝77°，则∠F＝.
14. （a2）﹣1（a﹣1b）3＝ ．15. 等腰三角形的一个角是70°，则它的另外两个角的度数是 ．16. 若（x+m）与（x+3）的乘积中不含x的一次项，则m＝.三、解答题
-
17. 计算：a÷b× ．18. 计算：（x+1）（x﹣1）﹣ ．19. 如图，在平面直角坐标系中，每个小正方形的边长均为1，点A的坐标为（﹣2，3）．点B的坐标为（﹣3，1），点C的坐标为（1，﹣2）．
⑴作出△ABC关于y轴对称的△A'B'C'．其中A'，B'，C'分别是A，B，C的对应点，不要求写作法；
⑵在x轴上找一点P，使得PB+PA的值最小．（不要求写作法）
20. 先化简，再求值：已知（+）÷ ， 其中x满足x2+2x﹣5＝0．21. 如图，在△ABC中，∠C＝90°，点D，点E在边BC上，且满足AD＝BD，AE平分∠BAD，若∠CAE＝42°．求∠AEC和∠B的度数．
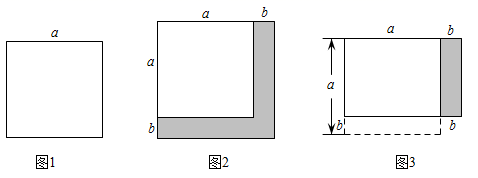
22. 某校组织八年级学生外出去博物馆参观，一部分学生步行，一部分学生骑车．已知骑车的路程是12km．而步行路程是骑车路程的 ． 若骑车的速度是步行学生速度的2倍，且骑车时间比步行所需时间少用20分钟，求骑车的平均速度．23. 如图，在四边形ABCD中，∠B=∠C= 90°，AB>CD，AD=AB+CD．
(1)、利用尺规作∠ADC的平分线DE，交BC于点E，连接AE． (保留作图痕迹，不写作法)(2)、在(1)的条件下，求证：AE⊥DE．24. 某地产公司为了吸引年轻人购房，持推出“主房+多变入户花园”的两种户型．即在图1中边长为a米的正方形主房进行改造．户型一是在主房两侧均加长b米（0＜9b＜a）．阴影部分作为入户花园，如图2所示．
户型二是在主房一边减少b米后，另一边再增加b米，阴影部分作为入户花园．如图3所示．
解答下列问题：
(1)、设两种户型的主房面积差为M，入户花园的面积差为N，试比较M和N的大小．(2)、若户型一的总价为50万元，户型二的总价为40万元，试判断哪种户型单价较低，并说明理由．25. 如图1，△ABC中，AB＝AC，∠BAC＝90°，点D是线段BC上一个动点，点F在线段AB上，且∠FDB＝∠ACB，BE⊥DF．垂足E在DF的延长线上．
(1)、如图2，当点D与点C重合时，试探究线段BE和DF的数量关系．并证明你的结论；(2)、若点D不与点B，C重合，试探究线段BE和DF的数量关系，并证明你的结论．