广东省广州市黄埔区2020-2021学年八年级上学期期末数学试题

试卷更新日期：2022-06-15 类型：期末考试

进入出卷网下载

一、单选题

1. 到△ABC的三个顶点距离相等的点是△ABC的（）

A、三边中线的交点 B、三条角平分线的交点 C、三边上高的交点 D、三边垂直平分线的交点

查看试题解析
2. 在平面直角坐标系中，点 $(2 ， - 1)$ 关于x轴对称的点是（）

A、 $(2 ， 1)$ B、 $(1， - 2)$ C、 $(- 1 ， 2)$ D、 $(- 2 ， - 1)$

查看试题解析
3. 已知一个多边形的内角和等于900º，则这个多边形是（）

A、五边形 B、六边形 C、七边形 D、八边形

查看试题解析
4. 下列各式从左到右的变形中，属于分解因式的是（）

A、a（m+n）＝am+an B、10x²﹣5x＝5x（2x﹣1） C、x²﹣16+6x＝（x+4）（x﹣4）+6x D、a²﹣b²﹣c²＝（a﹣b）（a+b）﹣c²

查看试题解析
5. 等腰三角形的一个内角为70°，则另外两个内角的度数分别是（）

A、55°，55° B、70°，40°或70°，55° C、70°，40° D、55°，55°或70°，40°

查看试题解析
6. 若a²+2a﹣1＝0，则 $\frac{a^{2}}{a - 2}$ （a﹣ $\frac{4}{a}$ ）的值是（）

A、﹣3 B、﹣1 C、1 D、3

查看试题解析
7. 若分式 $\frac{x^{2} - 1}{x + 1}$ 的值为0，则x的值为（）

A、0 B、1 C、﹣1 D、±1

查看试题解析
8. 如图，已知在△ABC中，CD是AB边上的高线，BE平分∠ABC，交CD于点E，BC=5，DE=2，则△BCE的面积等于（）

A、10 B、7 C、5 D、4

查看试题解析
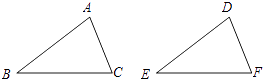
9. 如图，给出下列四组条件：
①AB=DE，BC=EF，AC=DF；
②AB=DE，∠B=∠E．BC=EF；
③∠B=∠E，BC=EF，∠C=∠F；
④AB=DE，AC=DF，∠B=∠E．
其中，能使△ABC≌△DEF的条件共有（）

A、1组 B、2组 C、3组 D、4组

查看试题解析
10.
如图，AD是△ABC的角平分线，DE⊥AC，垂足为E，BF∥AC交ED的延长线于点F，若BC恰好平分∠ABF，AE=2BF．给出下列四个结论：①DE=DF；②DB=DC；③AD⊥BC；④AC=3BF，其中正确的结论共有（　　）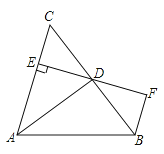

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

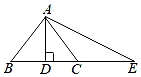
11. 分式 $\frac{1}{3 - x}$ 有意义时，x满足的条件是，分式方程 $\frac{1}{x} = \frac{4}{x + 3}$ 的解为．

查看试题解析
12. 计算：（﹣2x）³（﹣xy²）＝，（﹣ $\frac{2}{3}$ a⁵b⁷）÷ $\frac{3}{2}$ a⁵b⁵＝．

查看试题解析
13. 分解因式：2a（y﹣z）﹣3b（z﹣y）＝， x³y﹣xy＝．

查看试题解析
14. 如图，AD⊥BC，BD＝DC，点C在AE的垂直平分线上．若AB＝5cm，BC＝6cm，则AC＝， DE＝．

查看试题解析
15. 如图，在 $△$ ABC中，AB＝AC，∠A＝36 $°$ ， BD平分∠ABC，交AC于点D．则∠DBC＝， ∠BDC＝．

查看试题解析
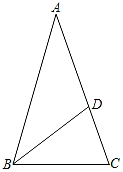16. 如图所示的三角形纸片中，AB＝8cm，BC＝6cm，AC＝5cm．沿过点B的直线折叠这个三角形，使点C落在AB边上的点E处，折痕为BD．则BE＝， $△$ ADE的周长等于．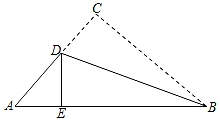

查看试题解析

三、解答题

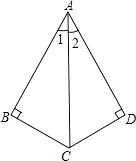
17. 先化简，再求值：（2x+y）²﹣（y﹣2x）² ，其中 $x = \frac{1}{3} ， y = - \frac{1}{4}$ ．

查看试题解析
18. 计算： $1 - \frac{x - y}{x + 2 y} \div \frac{x^{2} - y^{2}}{x^{2} + 4 x y + 4 y^{2}}$

查看试题解析
19. 解方程： $\frac{2}{x - 1} = \frac{4}{x^{2} - 1}$ ．

查看试题解析
20. 已知：如图，AB⊥BC，AD⊥DC，垂足分别为B，D，∠1=∠2．求证：AB=AD．

查看试题解析
21. 已知（a+b）²＝25，（a﹣b）²＝9．求a²﹣6ab+b² ．

查看试题解析
22. A、B两种型号的机器加工同一种零件，已知A型机器比B型机器每小时多加工20个零件，A型机器加工400个零件所用时间与B型机器加工300个零件所用时间相同，求A型机器每小时加工零件的个数．

查看试题解析
23. 如图，在 $△$ ABC中，∠ACB＝90°，∠A＝30°，BC＝4．

(1)、在题给的图中，按以下作法用直尺和圆规作图，并保留作图痕迹：
①以点C为圆心，CB长为半径作弧，交AB于点D；
②再分别以点B和点D为圆心，大于 $\frac{1}{2}$ BD的长为半径作弧，两弧相交于点E；
③作射线CE交AB于点F．

(2)、在你所作的图中，求AF．

查看试题解析
24. “综合与实践”学习活动准备制作一组三角形，记这些三角形的三边分别为a，b，c，并且这些三角形三边的长度为大于1且小于5的整数个单位长度．
$\frac{1}{单位长度}$

(1)、用记号（a，b，c）（a≤b≤c）表示一个满足条件的三角形，如（2，3，3）表示边长分别为2，3，3个单位长度的一个三角形．请列举出所有满足条件的三角形．

(2)、用直尺和圆规作出三边满足a＜b＜c的三角形（用给定的单位长度，不写作法，保留作图痕迹）．

查看试题解析
25. 已知：如图， AF平分∠BAC，BC⊥AF，垂足为E，点D与点A关于点E对称，PB分别与线段CF，AF相交于P，M．

(1)、求证：AB=CD；

(2)、若∠BAC=2∠MPC，请你判断∠F与∠MCD的数量关系，并说明理由．

查看试题解析