广东省佛山市顺德区2020-2021学年八年级上学期期末数学试题

试卷更新日期：2022-06-15 类型：期末考试

进入出卷网下载

一、单选题

1. 下列实数是无理数的是（）

A、 $\frac{1}{3}$ B、0.1010010001 C、 $π$ D、 $\sqrt{9}$

查看试题解析
2. 下列数据能作为直角三角形三边长的是（）

A、6，7，8 B、1， $\sqrt{3}$ ， 2 C、5，12，14 D、7，24，26

查看试题解析
3. 在平面直角坐标系中，点 $A$ 的坐标为 $(- 2 ， 3)$ ，则点 $A$ 关于 $y$ 轴对称点的坐标是（）

A、 $(- 2 ， - 3)$ B、 $(- 2 ， 3)$ C、 $(2 ， - 3)$ D、 $(2 ， 3)$

查看试题解析
4. 下列化简结果正确的是（）

A、 $- \sqrt{64} = - 8$ B、 $\sqrt{64} = \pm 8$ C、 $\sqrt{{(- 64)}^{2}} = - 64$ D、 $\pm \sqrt{64} = 8$

查看试题解析

5. 一家鞋店在一段时间内销售了某种女鞋30双，各种尺码的鞋销售量如下表：

尺码/ $cm$	22	22.5	23	23.5	24	24.5	25
销售量/双	1	2	5	10	4	6	2

店主决定在下次进货时增加一些 $23.5 cm$ 尺码的女鞋，影响店主决策的统计量是（）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析

6. 下列命题是真命题的是（）

A、如果 $a^{2} = b^{2}$ ，那么 $a = b$ B、直角坐标系中，与 $y$ 轴平行的一条直线上任意两点的横坐标相等 C、三角形的一个外角等于它的两个内角之和 D、1的平方根是1

查看试题解析
7. 在平面直角坐标系中，一次函数y=kx+b的图象如图所示，则k和b的取值范围是（）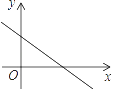

A、k＞0，b＞0 B、k＞0，b＜0 C、k＜0，b＞0 D、k＜0，b＜0

查看试题解析
8. 如图，当 $A D / / B C$ 时，下列结论正确的是（）

A、 $∠ 3 = ∠ 4$ B、 $∠ 2 = ∠ 4$ C、 $∠ 1 = ∠ 3$ D、 $∠ B = ∠ D$

查看试题解析
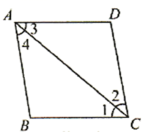9. 若方程 $m x + n y = 6$ 有两个解 ${\begin{array}{l} x = - 2 \\ y = 3 \end{array}$ 和 ${\begin{array}{l} x = 3 \\ y = - 2 \end{array}$ ，则 $m + n$ 的值为（）

A、12 B、-12 C、6 D、-6

查看试题解析
10. 如图表示一艘船从甲地航行到乙地，到达乙地后旋即返回．横坐标表示航行的时间，纵坐标表示船与甲地的距离．下列说法错误的是（）

A、船从甲地到乙地航行的速度比返航的速度更快 B、船从甲地航行到乙地的路程为 $s_{1}$ ，时间为 $t_{1}$ C、船往返的平均速度为 $\bar{v} = \frac{2 s_{1}}{t_{2}}$ D、 $t_{2}$ 表示船在返航时所用的时间

查看试题解析

二、填空题

11. 化简： $\sqrt[3]{8} =$ .

查看试题解析
12. 已知点 $A (\sqrt{2} ， y_{1})$ ， $B (\sqrt{3} ， y_{2})$ 在直线 $y = x$ 上，则 $y_{1}$ $y_{2}$ （填写<、=、>）．

查看试题解析
13. 一次函数 $y = 2 x + 6$ 的图象与 $y$ 轴的交点坐标是．

查看试题解析
14. 如图，在矩形 $O A B C$ 中， $O A = 2$ ， $O C = 1$ ， $O B = O D$ ，数轴上点 $D$ 所表示的数是．

查看试题解析
15. 如图， $D$ 为 $△ A B C$ 边 $A C$ 上一点，以点 $A$ 为圆心， $A D$ 为半径画弧，交 $B A$ 的延长线于点 $E$ ，连接 $E D$ ．若 $∠ B = 60 °$ ， $∠ C = 70 °$ ，则 $∠ A D E$ 的度数为．

查看试题解析
16. 小明和小丽同时到一家水果店买水果．小明买 $1 k g$ 苹果和 $2 k g$ 雪梨，共花了33元；小丽买 $2 k g$ 苹果和 $1 k g$ 雪梨，共花了36元．设苹果每千克 $x$ 元，雪梨每千克 $y$ 元，请根据题意，列出方程组：．

查看试题解析
17. 如图，在长方形 $A B C D$ 中， $A B = 4$ ， $B C = 8$ ，点 $E$ 是 $B C$ 边上一点，且 $A E = E C$ ，点 $P$ 是 $A D$ 边上一动点，连接 $P E$ 、 $P C$ ．给出下列结论：
① $B E = 3$ ；②当 $A P = 5$ 时， $A E / / C P$ ；③当 $A P = \frac{25}{6}$ 时， $A E$ 平分 $∠ B E P$ ；
④若 $∠ P B E = ∠ E P C$ ，则 $∠ B P C = ∠ P E C$ ．其中正确的是．

查看试题解析

三、解答题

18. 计算： $\sqrt{12} - \sqrt{\frac{4}{3}} \times \sqrt{15} + 2 \sqrt{5}$

查看试题解析
19. 解方程组： ${\begin{array}{l} 2 x + 3 y = 16 \\ x - y = 3 \end{array}$

查看试题解析
20. 一次函数 $y = - 2 x + 3$ ．

(1)、画出函数图象；

(2)、观察图象，写出函数的两个不同类型的特征．

查看试题解析
21. 某团体开展知识竞赛活动，甲队、乙队根据初赛成绩各选派6名队员参加复赛，两支队伍选出的6名选手复赛成绩分别如下：
甲队：65、80、85、85、95、100
乙队：65、90、80、100、100、75

(1)、根据数据填写下表，分析哪支队伍选手的复赛成绩较好；

平均数
中位数
众数
甲队
$a$
85
85
乙队
85
$b$
$c$

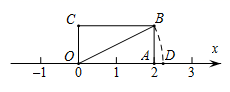
(2)、已知甲队6名选手复赛成绩的方差 ${S^{2}}_{甲} = 125$ ，请计算出乙队6名选手复赛成绩的方差，并判断哪支队伍的选手复赛成绩较为均衡．（ $S^{2} = \frac{1}{n} [{(x_{1} - \bar{x})}^{2} + {(x_{2} - \bar{x})}^{2} + \cdot \cdot \cdot + {(x_{n} - \bar{x})}^{2}]$ ）

查看试题解析
22. 如图， $l_{1}$ 反映了某公司产品的收入与销售量的关系， $l_{2}$ 反映了该公司产品的成本与销售量的关系，根据图象解决下列问题：

(1)、当销售量为2t时，收入=元，成本元，盈利为元；当销售量=t时，收入=成本；

(2)、求出盈利 $w$ 与销售量 $x$ 的函数表达式．

查看试题解析
23. 如图，点 $A$ 、 $B$ 、 $C$ 的坐标分别是 $A (- 1 ， 3)$ 、 $B (- 5 ， 1)$ 、 $C (0 ， 1)$ ．

(1)、判断 $△ A B C$ 的形状，并说明理由；

(2)、点 $P$ 是 $x$ 轴上的一动点，求出使得 $P A + P B$ 的值最小时点 $P$ 的坐标．

查看试题解析
24. 如图，在 $△ A B C$ 中， $A B = A C$ ， $D$ 是 $A C$ 边上的一点，连接 $B D$ 并延长到点 $E$ ，连接 $A E$ 、 $C E$ ， $A F$ 平分 $∠ B A C$ 交 $B D$ 于点 $F$ ．

(1)、若 $∠ B A C = 80 °$ ， $∠ F B C = 20 °$ ，求 $∠ A F D$ ；

(2)、给出下列三个关系：① $C E ⊥ B C$ ；② $B F = A E$ ；③ $A D = C D$ ．选取两个作为条件，一个作为结论构成一个真命题，写出这个真命题（用序号表示）；

(3)、证明（2）的结论．

查看试题解析
25. 如图，已知点 $A (2 ， - 5)$ 在直线 $l_{1}$ ： $y = 2 x + b$ 上， $l_{1}$ 和 $l_{2}$ ： $y = k x - 1$ 的图象交于点 $B$ ，且点 $B$ 的横坐标为8．

(1)、直接写出 $b$ 、 $k$ 的值；

(2)、若直线 $l_{1}$ 、 $l_{2}$ 与 $y$ 轴分别交于点 $C$ 、 $D$ ，点 $P$ 在线段 $B C$ 上，满足 $S_{△ B D P} = \frac{1}{4} S_{△ B D C}$ ，求出点 $P$ 的坐标；

(3)、若点 $Q$ 是直线 $l_{2}$ 上一点，且 $∠ B A Q = 45 °$ ，求出点 $Q$ 的坐标．

查看试题解析

	平均数	中位数	众数
甲队	$a$	85	85
乙队	85	$b$	$c$