广东省佛山市三水区2020-2021学年八年级上学期期末数学试题

试卷更新日期：2022-06-15 类型：期末考试

进入出卷网下载

一、单选题

1. 64的算术平方根是（）

A、±4 B、±8 C、4 D、8

查看试题解析
2. 下列几组数中，不能作为直角三角形三边长的是（）

A、5，12，13 B、9，40，41 C、0.5，1.2，1.3 D、2，3，4

查看试题解析
3. 在实数 $\frac{11}{3}$ ， 0， $\sqrt[3]{- 1}$ ， 3.1415926， $\sqrt{16}$ ， $4 . \overset{\cdot}{2} \overset{\cdot}{1}$ ， 3π中，有理数的个数为（）

A、3个 B、4个 C、5个 D、6个

查看试题解析
4. 三水是长寿之乡，以下能准确表示三水地理位置的是（）

A、在广州的西北方 B、东经113°，北纬23° C、距离广州40公里处 D、东经113°

查看试题解析
5. 如图，若 $A D / / B C$ ，则下列结论正确的是（）

A、 $∠ 1 = ∠ 3$ B、 $∠ 2 = ∠ 4$ C、 $∠ 1 = ∠ 2$ D、 $∠ 2 = ∠ 3$

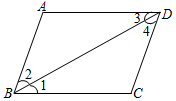查看试题解析
6. 有一组数据：15，14，16，16，18，17，19，21，20．这组数据的中位数是（）

A、16 B、17 C、18 D、19

查看试题解析
7. 直线y＝﹣3x与y＝﹣3x＋15的位置关系是（）

A、重合 B、平行 C、相交 D、无法判断

查看试题解析
8. 某网约车计费办法如图所示根据图象信息，下列说法正确的是（）

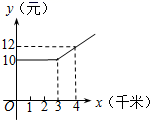A、该网约车起步价是12元 B、在3千米内只收12元 C、超过3千米（x＞3）部分每千米收费3元 D、超过3千米（x＞3）时所需费用y与x之间的函数关系式是y＝2x＋4

查看试题解析
9. 一种饮料有两种包装，2大盒、4小盒共装88瓶，3大盒、2小盒共装84瓶，大盒与小盒每盒各装多少瓶？设大盒装x瓶，小盒装y瓶，则可列方程组（）

A、 ${\begin{array}{l} 2 x + 4 y = 88 \\ 3 x + 2 y = 84 \end{array}$ B、 ${\begin{array}{l} 2 x + 4 y = 88 \\ 2 x + 3 y = 84 \end{array}$ C、 ${\begin{array}{l} 4 x + 2 y = 88 \\ 3 x + 2 y = 84 \end{array}$ D、 ${\begin{array}{l} 4 x + 2 y = 88 \\ 2 x + 3 y = 84 \end{array}$

查看试题解析
10. 正六边形ABCDEF在数轴上的位置如图，点A、F对应的数分别为0和1，若正六边形ABCDEF绕着顶点顺时针方向在数轴上连续翻转，翻转1次后，点E所对应的数为2，则连续翻转2021次后，数轴上2021这个数所对应的点是（）

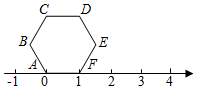A、A点 B、B点 C、C点 D、D点

查看试题解析

二、填空题

11. 比较大小： $5 \sqrt{3}$ $6 \sqrt{2}$ ．

查看试题解析
12. 如图所示，把长方形纸片ABCD纸沿对角线折叠，若∠BDE＝20°，那么∠BED＝．

查看试题解析
13. 命题“若a³＝b³ ，则a＝b”是(填“真”或“假”)命题．

查看试题解析
14. 已知 ${\begin{matrix} x = 4 \\ y = m \end{matrix}$ 是二元一次方程7x+2y＝10的一组解，则m的值是.

查看试题解析
15. 若|a-4|+(b+3)²=0，则A（a，b）关于y轴对称点的坐标为．

查看试题解析
16. 如图，这是一个供滑板爱好者使用的U型池的示意图，该U型池可以看成是长方体去掉一个“半圆柱”而成，中间可供滑行部分的截面是直径为 $\frac{32}{π}$ m的半圆，其边缘AB＝CD＝15m ，点E在CD上，CE＝3m ，一滑板爱好者从A点滑到E点，则他滑行的最短距离约为m ．（边缘部分的厚度忽略不计）

查看试题解析
17. 如图，若AB∥CD，AB⊥AF，E是AF的中点，AF＝14，BD＝50，CD＝30，则CF＝．

查看试题解析

三、解答题

18. 计算：（﹣1）²⁰²⁰+ $\sqrt{9}$ ﹣π⁰+ $\sqrt{\frac{1}{8}} \times \sqrt{32}$ ．

查看试题解析
19. 解方程组： ${\begin{array}{l} 4 x + y = - 12 \\ 3 x - 4 y = 105 \end{array}$ ．

查看试题解析
20. 如图，在平面直角坐标系中，网格中每一个小正方形的边长都是1个单位长度．

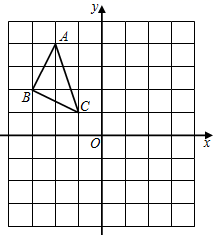(1)、画出△ABC关于y轴对称的图形△A′B′C′，写出C的坐标；

(2)、求△ABC中AC边上的高．

查看试题解析
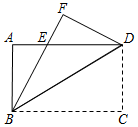
21. 进入夏季，为了解某品牌电风扇销售量的情况，厂家对某商场7月份该品牌甲、乙、丙三种型号的电风扇销售量进行统计，绘制如下两个统计图（均不完整）.请你结合图中的信息，解答下列问题：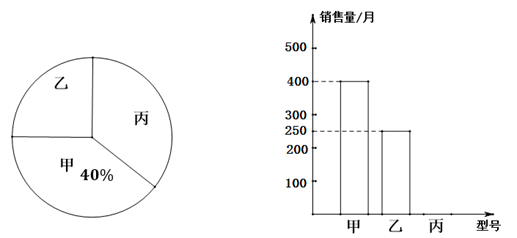

(1)、该商场7月份售出这种品牌三种型号的电风扇共多少台？补全条形统计图.

(2)、若该商场计划订购这三种型号的电风扇共5000台，根据7月份销售量的情况，求该商场应订购丙种型号电风扇多少台比较合理？

查看试题解析
22. 三水九道谷漂流项目深受欢迎，在景区游船放置区，工作人员把偏离的游船从点A拉回点B的位置（如图）．在离水面高度为8m的岸上点C，工作人员用绳子拉船移动，开始时绳子AC的长为17m，经过10秒后游船移动到点D的位置，此时BD＝6m，问工作人员拉绳子的速度是多少？

查看试题解析
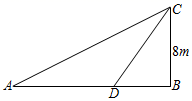23. 如图，四边形ABCD是长方形，AD∥BC．点F是DA延长线上一点，点G是CF上一点，并且∠ACG＝∠AGC，∠GAF＝∠F．则∠ECB与∠ACB有什么数量关系？为什么？

查看试题解析
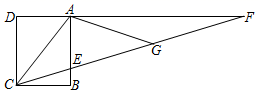24. 我国重视农村扶贫，在国家政策的引导下，乡村经济发展迅速，四川某农家的高山苹果通过网店销往全国，苹果被分级包装销售，相关信息如表所示：
苹果种类
一级
二级
包装规格（kg/盒）
5
10
利润（元/盒）
35
32

(1)、若该农家今年十月份售出两种等级苹果共150盒，获得利润4950元，求十月份该农家销售一级苹果多少盒．

(2)、根据之前的销售情况，估计今年十一月份能售出两种规格苹果共2000千克，一级苹果的产量不多于800千克，设销售一级苹果t（kg），销售完两种等级苹果获得的总利润为T（元），求出T与t之间的函数关系式，并求销售完十一月份生产的两种苹果最多获利多少元？

查看试题解析
25. 如图①，平面直角坐标系中，直线y＝kx＋b与x轴交于点A（﹣10，0），与y轴交于点B，与直线y＝﹣ $\frac{7}{3}$ x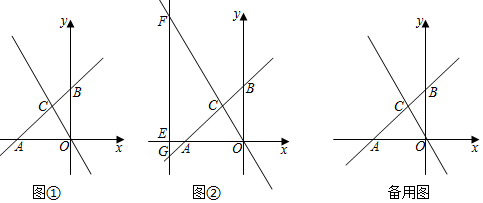交于点C（a，7）.

(1)、求点C的坐标及直线AB的表达式；

(2)、如图②，在（1）的条件下，过点E作直线l⊥x轴，交直线y＝﹣ $\frac{7}{3}$ x于点F，交直线y＝kx＋b于点G，若点E的坐标是（﹣15，0）.
①求△CGF的面积；
②点M为y轴上OB的中点，直线l上是否存在点P，使PM﹣PC的值最大？若存在，直接写出这个最大值；若不存在，说明理由；

(3)、若（2）中的点E是x轴上的一个动点，点E的横坐标为m（m＜0），点E在x轴上运动，当m取何值时，直线l上存在点Q，使得以A，C，Q为顶点的三角形与△AOC全等？请直接写出相应的m的值.

查看试题解析

苹果种类	一级	二级
包装规格（kg/盒）	5	10
利润（元/盒）	35	32