广东省潮州市2020-2021学年八年级上学期期末数学试题

试卷更新日期：2022-06-15 类型：期末考试

进入出卷网下载

一、单选题

1. 改革开放以来，我国众多科技实体在各自行业取得了举世瞩目的成就，大疆科技、华为集团、太极股份和凤凰光学等就是其中的杰出代表．上述四个企业的标志是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 医学研究发现某病毒直径约为 $0.000043$ 毫米，这个数用科学记数法表示为 $($ $)$

A、 $0.43 \times 10^{4}$ B、 $4.3 \times 10^{- 5}$ C、 $0.43 \times 10^{- 4}$ D、 $0.43 \times 10^{5}$

查看试题解析
3. 下列运算正确的是（）

A、 ${(a^{2} b)}^{3} = a^{5} b^{3}$ B、a⁶÷a²＝a³ C、5y³•3y²＝15y⁵ D、a+a²＝a³

查看试题解析
4. 当 $x = 1$ 时，下列分式没有意义的是（）

A、 $\frac{x + 1}{x}$ B、 $\frac{x}{x - 1}$ C、 $\frac{x - 1}{x}$ D、 $\frac{x}{x + 1}$

查看试题解析
5. 在下列各式中，不能用平方差公式计算的是（）

A、 $(A + B) (A - B)$ B、 $(α - β) (β + α)$ C、 $(- a - b) (b + a)$ D、 $(- x + y) (y + x)$

查看试题解析
6. 当 $a = 3 ， b = - 2$ 时，代数式 $a^{2} + 2 a b + b^{2}$ 的值是（）

A、-7 B、1 C、17 D、25

查看试题解析
7. $6 x^{3} y^{2} - 3 x^{2} y^{3}$ 分解因式时，应提取的公因式是 $($ $)$

A、3xy B、3x²y C、 $3 x^{2} y^{3}$ D、 $3 x^{2} y^{2}$

查看试题解析
8. 根据分式的基本性质，分式 $\frac{- a}{a - b}$ 可变形为（）

A、 $\frac{a}{- a - b}$ B、 $\frac{a}{a + b}$ C、 $- \frac{a}{a - b}$ D、 $- \frac{a}{a + b}$

查看试题解析
9. 为响应承办“绿色奥运”的号召，九年级（1）班全体师生义务植树300棵．原计划每小时植树x棵，但由于参加植树的全体师生植树的积极性高涨，实际工作效率提高为原计划的1.2倍，结果提前20分钟完成任务．则下面所列方程中，正确的是（）

A、 $\frac{300}{x} - \frac{20}{60} = \frac{300}{1.2 x}$ B、 $\frac{300}{x} - \frac{300}{1.2 x} = 20$ C、 $\frac{300}{x} - \frac{300}{x + 1.2 x} = \frac{20}{60}$ D、 $\frac{300}{x} = \frac{300}{1.2 x} - \frac{20}{60}$

查看试题解析
10.
如图，AD是△ABC的角平分线，DE⊥AC，垂足为E，BF∥AC交ED的延长线于点F，若BC恰好平分∠ABF，AE=2BF．给出下列四个结论：①DE=DF；②DB=DC；③AD⊥BC；④AC=3BF，其中正确的结论共有（　　）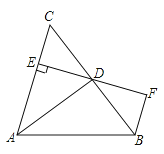

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

11. 当 $x =$ 时，分式 $\frac{x^{2} - 4}{x - 2}$ 值为零.

查看试题解析
12. 在平面直角坐标系中，点A的坐标是(2，- 3)，作点A关于x轴的对称点，得到点A'，再作点A'关于y轴的对称点，得到点A″，则点A″的坐标是.

查看试题解析
13. 分解因式： $a b^{3} - 4 a b$ =.

查看试题解析
14. 如图所示，在 $Δ A B C$ 中， $∠ C = 90 ° ， D E ⊥ A B$ 于点 $E ， A C = A E$ ，且 $∠ C D A = 55 °$ ，则 $∠ B =$ 度．

查看试题解析
15. 如图，∠1、∠2、∠3、∠4是五边形ABCDE的4个外角，若∠A=100°，则∠1+∠2+∠3+∠4= ．

查看试题解析
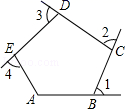16. 式子 $| \begin{array}{l} a \\ c \end{array} \begin{array}{l} b \\ d \end{array} |$ 称为二阶行列式，规定它的运算法则为 $| \begin{array}{l} a \\ c \end{array} \begin{array}{l} b \\ d \end{array} | = a d - b c$ ，则二阶行列式 $| \begin{array}{l} a^{2} - a \\ a \end{array} \begin{array}{l} 1 \\ \frac{1}{a^{2} - 1} \end{array} | =$ ．

查看试题解析
17. 已知关于x的分式方程 $\frac{x}{x - 3} - 2 = \frac{k}{x - 3}$ 有一个正数解，则k的取值范围为.

查看试题解析

三、解答题

18. 计算： ${(- 3)}^{0} + {(\frac{1}{2})}^{- 1} - \sqrt{9} - | - 2 |$

查看试题解析
19. 2020年1月份，某药店计划购进一批甲、乙两种型号的口罩，已知一袋甲种口罩的进价与一袋乙种口罩的进价和为40元，用90元购进甲种口罩的袋数与用150元购进乙种口罩的袋数相同．求每袋甲种、乙种口罩的进价分别是多少元？

查看试题解析
20. 已知 $x^{2} + 8 x - 7 = 0$ ，求 $(x + 2) (x - 2) - 4 x (x - 1) + (2 x + 1)^{2}$ 的值.

查看试题解析
21. 线段 $A B$ 与射线 $A P$ 有一公共端点 $A$ ．完成下列作图，不要求写作法，保留作图痕迹．
⑴用直尺和圆规作出 $∠ B A P$ 的角平分线 $A C$ ．
⑵用圆规在射线 $A P$ 上截取线段 $A D = A B$ ，连接 $B D$ ．
⑶用直尺和圆规在 $B D$ 右侧作出以点 $B$ 为顶点的 $∠ D B Q$ ，使 $∠ D B Q = ∠ B D A$ ，且 $B Q$ 与 $A C$ 相交于点 $Q$ ．

查看试题解析
22. 已知 $a \neq 0$ ， $a + b \neq 0$ 且 $a - b = 1$ ，求代数式 $\frac{a^{2} - b^{2}}{2 a^{2} + 2 a b} \div (a - \frac{2 a b - b^{2}}{a})$ 的值.

查看试题解析
23. 如图，在等边三角形 $A B C$ 中， $D$ 是 $A B$ 上的一点， $E$ 是 $C B$ 延长线上一点，连接 $C D 、 D E ，$ 已知 $∠ E D B = ∠ A C D ， B C = 6$ ，

(1)、求证： $Δ D E C$ 是等腰三角形

(2)、当 $∠ B D C = 5 ∠ E D B ， E C = 8 ， A D = 2$ 时，求 $Δ E D C$ 的面积．

查看试题解析
24. 有一列按一定顺序和规律排列的数：
第一个数是 $\frac{1}{1 \times 2}$ ；第二个数是 $\frac{1}{2 \times 3}$ ；第三个数是 $\frac{1}{3 \times 4}$ ；
对任何正整数 $n$ ，第 $n$ 个数与第 $(n + 1)$ 个数的和等于 $\frac{2}{n \times (n + 2)}$

(1)、经过探究，我们发现： $\frac{1}{1 \times 2} = \frac{1}{1} - \frac{1}{2}$ ， $\frac{1}{2 \times 3} = \frac{1}{2} - \frac{1}{3}$ ， $\frac{1}{3 \times 4} = \frac{1}{3} - \frac{1}{4}$
设这列数的第 $5$ 个数为 $a$ ，那么① $a > \frac{1}{5} - \frac{1}{6}$ ；② $a = \frac{1}{5} - \frac{1}{6}$ ， ③ $a < \frac{1}{5} - \frac{1}{6}$ ，则正确（填序号）．

(2)、请你观察第 $1$ 个数、第 $2$ 个数、第 $3$ 个数，猜想这列数的第 $n$ 个数可表示 ▲ （用含 $n$ 的式子表示），并且证明：第 $n$ 个数与第 $(n + 1)$ 个数的和等于 $\frac{2}{n \times (n + 2)}$ ；

(3)、利用上述规律计算： $\frac{1}{2020 \times 2018} + \frac{1}{2018 \times 2016} + \frac{1}{2016 \times 2014} + \cdot \cdot \cdot + \frac{1}{4 \times 2}$ 的值．

查看试题解析
25. 通过对下面数学模型的研究学习，解决下列问题：

(1)、（模型呈现）如图1， $∠ B A D = 90 °$ ， $A B = A D$ ，过点 $B$ 作 $B C ⊥ A C$ 于点 $C$ ，过点 $D$ 作 $D E ⊥ A C$ 于点 $E$ .由 $∠ 1 + ∠ 2 = ∠ 2 + ∠ D = 90 °$ ，得 $∠ 1 = ∠ D$ .又 $∠ A C B = ∠ A E D = 90 °$ ，可以推理得到 $Δ A B C ≌ Δ D A E$ .进而得到 $A C =$ ， $B C =$ .我们把这个数学模型称为“ $K$ 字”模型或“一线三等角”模型；

(2)、（模型应用）①如图2， $∠ B A D = ∠ C A E = 90 °$ ， $A B = A D$ ， $A C = A E$ ，连接 $B C$ ， $D E$ ，且 $B C ⊥ A F$ 于点 $F$ ， $D E$ 与直线 $A F$ 交于点 $G$ .求证：点 $G$ 是 $D E$ 的中点；
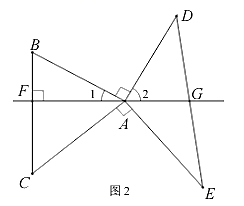
②如图3，在平面直角坐标系 $x O y$ 中，点 $A$ 的坐标为 $(2 ， 4)$ ，点 $B$ 为平面内任一点.若 $Δ A O B$ 是以 $O A$ 为斜边的等腰直角三角形，请直接写出点 $B$ 的坐标.

查看试题解析