山东省淄博市沂源县2021-2022学年七年级上学期期中数学试题

试卷更新日期：2022-06-15 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各组数是勾股数的是（）

A、5、12、13 B、6、8、12 C、4、5、6 D、8、24、25

查看试题解析
2. 下列四个图形中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下面四个图形中，线段BE是⊿ABC的高的图是（）

A、 B、 C、 D、

查看试题解析
4. 下列四种图形都是轴对称图形，其中对称轴条数最多的图形是( )

A、等边三角形 B、矩形 C、菱形 D、正方形

查看试题解析
5. 下列说法中，正确的是（）

A、全等图形是形状相同的两个图形 B、全等三角形是指面积相同的两个三角形 C、等边三角形都是全等三角形 D、全等图形的周长、面积都相等

查看试题解析
6.
如图所示，以直角三角形的三边分别向外作正方形，其中两个以直角边为边长的正方形面积分别为225和400，则正方形 $A$ 的面积是（）

A、175 B、575 C、625 D、700

查看试题解析
7. 有以下四个说法：①两边和其中一边上的中线（或第三边上的中线）对应相等的两个三角形全等；②两角和其中一角的角平分线（或第三角的角平分线）对应相等的两个三角形全等；③两边和其中一边上的高（或第三边上的高）对应相等的两个三角形全等．其中正确的有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
8. 下列条件中，不能判断△ABC≌△DEF 的是（）

A、∠A＝∠E，BA＝EF，AC＝FD B、∠B＝∠E，BC＝EF，高 AH＝DG C、∠C＝∠F＝90°，∠A＝60°，∠E＝30°，AC＝DF D、∠A＝∠D，AB＝DE，AC＝DF

查看试题解析
9. 已知 $△ A B C$ 中， $A B = A C = 10$ ， BD是AC边上的高线，DC=2，那么BD等于（）

A、2 B、4 C、6 D、8

查看试题解析
10. 如图，在 $R t △ A B C$ 中， $∠ B = 90 °$ ， ED是AC的垂直平分线，交AC于点 $D$ ，交 $B C$ 于点 $E$ ．已知 $∠ B A E = 10 °$ ，则 $∠ C$ 的度数为（）

A、 $40 °$ B、 $50 °$ C、 $60 °$ D、 $70 °$

查看试题解析
11. 在△ABC中，已知点D、E、F分别是BC、AD、CE的中点，且S_△ABC=4 cm² ，则S_△BEF=（　　）

A、2 cm² B、1cm² C、0.5cm² D、0.25 cm²

查看试题解析
12. 如图为正方形网格，则∠1+∠2+∠3=（）

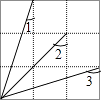A、105° B、120° C、115° D、135°

查看试题解析

二、填空题

13. 在 $△ A B C$ 中， $∠ A = ∠ C = \frac{1}{3} ∠ B$ ，则这个三角形是三角形（填“锐角”或“直角”或“钝角”）．

查看试题解析
14. 如图，一棵大树在一次强台风中于离地面 $3 m$ 处折断倒下，树干顶部在距离根部 $4 m$ 处，这棵大树在折断前的高度为 $m$ .

查看试题解析
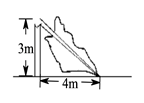15. 小强站在镜前，从镜中看到镜子对面墙上挂着的电子钟，则如图所示的电子钟的实际时刻是．

查看试题解析
16. 如图，D为 $△ A B C$ 的边AC上一点， $A B = A C$ ， $B C = C D$ ， $∠ A B D = 15 °$ ，则 $∠ A =$ °．

查看试题解析
17. △ABC中，∠C=90°，AC=BC，分别过A、B向过C的直线CD作垂线，垂足分别为E、F，若AE=5，BF=3，则EF＝．

查看试题解析

三、解答题

18. 如图，在 $10 \times 10$ 的正方形网格中，每个小正方形的边长都为1，网格中有一个格点 $△ A B C$ （即三角形的顶点都在格点上）．在图中作出 $△ A B C$ 关于直线l对称的 $△ A_{1} B_{1} C_{1}$ （要求：A与 $A_{1}$ ， B与 $B_{1}$ ， C与 $C_{1}$ 相对应）．

查看试题解析
19. 为了向国庆献礼，某校各班都在开展丰富多彩的庆祝活动，八年级（3）班开展了手工制作竞赛，每个同学都在规定时间内完成一件手工作品．陈莉同学在制作手工作品的第一、二个步骤是：①先裁下了一张长 $B C = 20 c m$ ，宽 $A B = 16 c m$ 的矩形纸片ABCD，②将纸片沿着直线AE折叠，点D恰好落在BC边上的F处，…请你根据①②步骤解答下列问题：

(1)、找出图中与 $∠ F E C$ 相等的角；

(2)、计算EC的长．

查看试题解析
20. 如图，一架长5m的梯子AB斜立在一竖直的墙上，这时梯子底端距墙底3m，如果梯子的顶端沿墙下滑1 m，梯子的底端在水平方向沿一条直线也将滑动1 m吗？用所学知识论证你的结论．

查看试题解析
21. 如图， $△ A B C$ 和 $△ A^{'} B^{'} C^{'}$ 关于直线 $M N$ 对称， $△ A^{'} B^{'} C^{'}$ 和 $△ A^{″} B^{″} C^{″}$ 关于直线 $E F$ 对称．
⑴画出直线 $E F$ ；
⑵直线 $M N$ 与 $E F$ 相交于点O，试探究 $∠ B O B^{″}$ 与直线 $M N$ 、 $E F$ 所夹锐角 $α$ 的数量关系．

查看试题解析
22. 如图，在四边形ABCD中，AD=DC，DF是∠ADC的平分线，AF∥BC，连接AC，CF.求证：CA是∠BCF的平分线.

查看试题解析
23. 两个大小不同的等腰直角三角板按图①所示的位置放置，图②是由它抽象画出的几何图形， $A B = A C$ ， $A E = A D$ ， $∠ B A C = ∠ E A D = 90 °$ ， $B$ ， $C$ ， $E$ 在同一条直线上，连接 $D C$ .

(1)、请找出图②中与 $Δ A B E$ 全等的三角形，并给予证明(说明：结论中不得含有未标识的字母)；

(2)、求证： $D C ⊥ B E$ .

查看试题解析
24. 已知：如图所示，直线 $M A ∥ N B$ ， $∠ M A B$ 与 $∠ N B A$ 的平分线交于点C，过点C作一条直线l与两条直线MA、NB分别相交于点D、E．

(1)、如图1所示，当直线l与直线MA垂直时，猜想线段AD、BE、AB之间的数量关系，请直接写出结论，不用证明；

(2)、如图2所示，当直线l与直线MA不垂直且交点D、E都在AB的同侧时，（1）中的结论是否成立？如果成立，请证明；如果不成立，请说明理由；

(3)、当直线l与直线MA不垂直且交点D、E在AB的异侧时，（1）中的结论是否仍然成立？如果成立，请说明理由；如果不成立，那么线段AD、BE、AB之间还存在某种数量关系吗？如果存在，请直接写出它们之间的数量关系．

查看试题解析