山东省青岛市即墨区2021-2022学年七年级上学期期中数学试题

试卷更新日期：2022-06-15 类型：期中考试

进入出卷网下载

一、单选题

1. $- \frac{1}{2021}$ 的相反数是（）

A、2021 B、-2021 C、 $\frac{1}{2021}$ D、 $- \frac{1}{2021}$

查看试题解析
2. 某一品牌的牛奶包装盒，该包装盒可以近似的看成是长方体，则它的展开图不可能是（）

A、 B、 C、 D、

查看试题解析
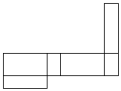3. 下列运算中，正确的是（）

A、（﹣56）÷（﹣7）＝﹣8 B、2a+3b＝5ab C、 $(- \frac{2}{3})^{3} = - \frac{8}{9}$ D、9a﹣8a＝a

查看试题解析
4. 下列说法中，正确的是（）

A、有理数分为正数和负数 B、绝对值是自身的数是0 C、互为相反数的两个数的绝对值相等 D、如果两个数的绝对值相等，那么这两个数相等

查看试题解析
5. 下列各式中，与代数式a+b﹣c的值相等的足（）

A、a﹣（b+c） B、a+（b﹣c） C、（a﹣b）+c D、a+（c﹣b）

查看试题解析
6. 实数a、b、c在数轴上的位置如图所示，且a与c互为相反数，则下列式子中一定成立的是（）

A、a+b+c>0 B、|a+b|<c C、|a-c|=|a|+c D、ab<0

查看试题解析
7.
如图是一块带有圆形空洞和方形空洞的小木板，则下列物体中既可以堵住圆形空洞，又可以堵住方形空洞的是( )

A、 B、 C、 D、

查看试题解析
8. 已知a，b满足|a﹣3|+（b+2）²＝0，则单项式﹣5ax^a﹣by的系数和次数分別是（）

A、﹣15，6 B、﹣15，5 C、﹣5，6 D、﹣5，5

查看试题解析

二、填空题

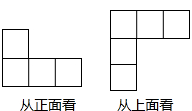
9. 我国南海某海域探朋可然冰储量约有194亿立方米，194亿用科学记数法表示为．

查看试题解析
10. 夏天打开冰箱冷冻室门时常会看到一团“白雾”．这是因为夏天空气温度较高，冰箱内外部温差较大，空气中的水蒸气遇冷凝结成小水滴而形成的．假设夏天空气温度是32℃，而冰箱冷冻室的温度是﹣16℃，那么此时的温差是 ℃．

查看试题解析
11. 定义一种新运算“⊕”如下：当a≥b时，a⊕b＝ab；当a＜b时，a⊕b＝a².则当x＝﹣2时，（3⊕x）•x的值为．

查看试题解析
12. 比较大小：0 $- \frac{2020}{2021}$ ；|﹣ $5^{2}$ | $(- 5)^{2}$ ．（用“＞，＜或＝”填空）

查看试题解析
13. 一个直九棱柱底面的每条边长都等于3cm，侧边长都等于6cm，则它的侧面面积等于 cm² ．

查看试题解析
14. 已知代数式2x²﹣3x的值为﹣5，那么代数式2021﹣4x²+6x的值为．

查看试题解析
15. 一个几何体由若干个大小相同点小立方块搭成，如图分别是从它的正面、上面看到的形状图，该几何体至少是用块小立方块搭成的.

查看试题解析
16. 有理数a、b、c均不为0，且a+b+c＝0，设x＝ $\frac{| a |}{b + c} + \frac{| b |}{c + a} + \frac{| c |}{a + b}$ ，则代数式x²⁰²¹+2021x﹣2021的值为．

查看试题解析

三、解答题

17. 一个几何体由大小相同的立方块搭成，从上面看到的形状如图所示，其中小正方形中的数字表示在该位置的立方块个数．

(1)、在所给的方框中分别画出该儿何体从正面，从左面看到的形状图；

(2)、若允许从该几何体中拿掉部分立方块，使剩下的几何体从正面看到的形状图和原几何体从正面看到的形状图相同，则最多可拿掉个立方块．

查看试题解析
18. 计算

(1)、﹣76﹣（+67）+76﹣（﹣43）

(2)、 $(- 24) \div (\frac{1}{2} - \frac{2}{3} - 1 \frac{1}{6})$

(3)、 $(- 2)^{4} - 3 \div (- \frac{1}{3}) \times (- 2)$

(4)、（﹣3）³+3×（﹣1）¹⁰﹣（﹣4）×6

查看试题解析
19. 化简：

(1)、2a﹣3b﹣4﹣5a+6﹣7b

(2)、2a²b﹣ $\frac{1}{2} (12 a b^{2} - 6 a^{2} b) + 3 (a b^{2} - 2 a^{2} b)$

查看试题解析
20. 先化简，再求值：
求（2xy²﹣3x³﹣1）﹣2（x³﹣3xy²+1）的值，其中x＝﹣2，xy＝﹣6．

查看试题解析
21. 某人用400元购头了8套儿童服装，准备以一定价格出售，如果以每套儿童服装58元的价格为标准，超出的记作正数，不足的记作负数，记录如下：+4，﹣5，+2，+1，﹣3，﹣2，0，﹣1．（单位：元）

(1)、当他卖完这八套儿童服装后是盈利还是亏损？

(2)、盈利（或亏损）了多少钱？

查看试题解析
22. 小颖为妈妈准备了一份生日礼物，礼物外包装盒为长方体形状，长、宽、高分别为 a、b、c（a>b>c），为了美观，小颖决定在包装盒外用丝带打包装饰，她发现，可以用如图所示的三种打包方式，所需丝带的长度分别为?₁ ， ?₂ ， ?₃（不计打结处丝带长度）.

(1)、用含a、b、c 的代数式分别表示?₁ ， ?₂ ， ?₃；

(2)、请帮小颖选出最节省丝带的打包方式，并说明理由.

查看试题解析
23. 阅读材料：
在数轴上，点A在原点O的左边，距离原点4个单位长度，点B在原点的右边，点A和点B之间的距离为14个单位长度．

(1)、点A表示的数是，点B表示的数是；

(2)、点A、B同时出发沿数轴向左移动，速度分别为2个单位长度/秒，4个单位长度/秒，经过多少秒，点A与点B重合？

(3)、点M、N分别从点A、B出发沿数轴向右移动，速度分别为1个单位长度/秒、2个单位长度/秒，点P也为数轴上一点，并且总保持OP＝NP．设OP﹣AM的值为y，在移动过程中，y值是否发生变化？若不变，求出y值；若变化，说明理由．

查看试题解析