山东省济宁市任城区2021-2022学年七年级上学期期中数学试题
试卷更新日期：2022-06-15 类型：期中考试
一、单选题
-
1. 下列轴对称图形中，有4条对称轴的图形是（ ）A、
B、
C、
D、
-
2. 下列长度的三条线段，能组成三角形的是（ ）A、2，3，4 B、2，3，5 C、2，2，4 D、2，2，5
-
3. 如图所示，三角形纸片被正方形纸板遮住了一部分，小明根据所学知识画出了一个与该三角形完全重合的三角形，那么这两个三角形完全重合的依据是（ ）
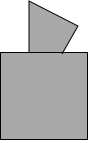A、SSS B、SAS C、AAS D、ASA -
4. 等腰三角形的一个角是50°，则它顶角的度数是（ ）A、80°或50° B、80° C、80°或65° D、65°
-
5. 下列各组数中，以它们为边长的线段不能构成直角三角形的是（ ）A、3，4，5 B、13，5，12 C、0.3，0.4，0.5 D、2，3，4
-
6. 如图所示的图形中， 于 ，线段AE是几个三角形的高（ ）．
A、3 B、4 C、5 D、6 -
7. 如图，Rt△ABC中，∠C=90°，AD平分∠BAC，交BC于点D，AB=10，S△ABD=15，则CD的长为（ ）
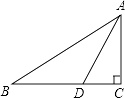A、3 B、4 C、5 D、6 -
8. 如图所示，正方形 和正方形 的面积分别是100和36，则以 为直径的半圆的面积是（ ）
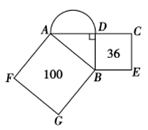A、 B、 C、 D、 -
9.
如图，桌面上有M、N两球，若要将M球射向桌面的任意一边，使一次反弹后击中N球，则4个点中，可以瞄准的是（ ）
A、点A B、点B C、点C D、点D
二、填空题
-
10. 如图，在一个长为8cm，宽为5cm的长方形草地上，放着一根长方体的木块，它的棱和草地宽AD平行且棱长大于AD，木块从正面看是边长为2cm的正方形，一只蚂蚁从点A处到达点C处需要走的最短路程是 ．
-
11. 如图，要测量水池宽 ，可从点 出发在地面上画一条线段 ，使 ，再从点 观测，在 的延长线上测得一点 ，使 ，这时量得 ，则水池宽 的长度是 m．
-
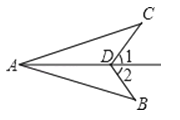
12.
如图，∠1=∠2，要使△ABD≌△ACD，需添加的一个条件是 （只添一个条件即可）．
-
13. 如图，四边形ABCD中，AB∥CD，AD∥BC，且∠BAD、∠ADC的角平分线AE、DF分别交BC于点E、F．若EF＝2，AB＝5，则AD的长为 ．
-
14.
如图，Rt△ABC中，∠B=90°，AB=4，BC=3，AC的垂直平分线DE分别交AB，AC于D，E两点，则CD的长为 ．
-
15. 如图，在△ABC中，AB＝AC，BC＝5，△ABC的面积为20，DE垂直平分AC，分别交边AB，AC于点D，E，点F为直线DE上一动点，点G为BC的中点，连接FG，FC，则FC＋FG的最小值为 ．
三、解答题
-
16. 如图，AB＝AC，AD为△ABC的BC边上的中线，△ABD与△ACD全等吗？为什么？
-
17. 如图，AD是∠BAC的平分线，CE是△ADC边AD上的高，若∠BAC＝80°，∠ECD＝25°，求∠ACB的度数．
-
18. 在△ABC中，D是BC上一点，AB=10，BD=6，AD=8，AC=17，求△ABC的面积．
-
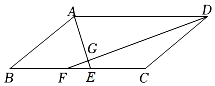
19. 如图，△ABC和△A′B′C′的顶点都在边长为1的正方形网格的格点上，且△ABC和△A′B′C′关于直线m成轴对称．
(1)、直接写出△ABC的面积；(2)、请在如图所示的网格中作出对称轴m． -
20. 如图，已知∠A＝∠E，AB＝EB，点D在AC边上，且∠ABE＝∠CBD．
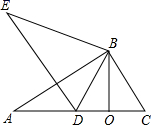(1)、求证：△EBD≌△ABC．(2)、如果O为CD中点，∠BDE＝65°，求∠OBC的度数． -
21. 如图，高速公路上有A，B两点相距10km，C，D为两村庄，已知DA＝4km，CB＝6km，DA⊥AB于点A，CB⊥AB于B，现要在AB上建一个服务站E，使得C，D两村庄到E站的距离相等，求BE的长．
-
22. 如图，分别过点 、 作 的 边上的中线 及其延长线的垂线，垂足分别为 、 .
(1)、求证： ；(2)、若 的面积为4， 的面积为3，求△ABF的面积. -
23. 如图，在△ABC中，∠C＝90°，点P是线段AC上一点．
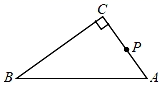(1)、在线段AB上取一点D，使PD＝PA，作BD的垂直平分线交BC于点E，交BD于点F（要求尺规作图，保留作图痕迹，不写作法）；(2)、在（1）所作的图中，连接PD，DE，求证：DE⊥DP． -
24. 如图，两个等腰直角△ABC和△CDE中，∠ACB＝∠DCE＝90°．
(1)、观察猜想如图1，点E在BC上，线段AE与BD的数量关系是 ， 位置关系是 ．(2)、探究证明把△CDE绕直角顶点C旋转到图2的位置，（1）中的结论还成立吗？说明理由．
