辽宁省锦州市凌海市2021-2022学年七年级上学期期中数学试题

试卷更新日期：2022-06-15 类型：期中考试

进入出卷网下载

一、单选题

1. $- \frac{1}{3}$ 的倒数是（）

A、3 B、-3 C、 $\frac{1}{3}$ D、 $- \frac{1}{3}$

查看试题解析
2. 观察下图，把左边的图形绕着给定的直线旋转一周后，可能形成的立体图形是（）

A、 B、 C、 D、

查看试题解析
3. 下列说法正确的是（）

A、有理数中有最大的数 B、0是整数中最小的数 C、有理数中绝对值最小的数是0 D、若一个数的平方与立方的结果相等，则这个数是0

查看试题解析
4. 数轴上表示 $m$ 、 $n$ 、 $p$ 三个数的点的位置如图所示，则下列结论错误的是（）

A、 $m = 1$ B、 $n < m$ C、 $n > p$ D、 $p > m$

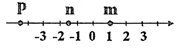查看试题解析
5. 2020年6月23日，我国成功发射北斗系统第55颗导航卫星，暨北斗三号最后一颗全球组网卫星，该卫星驻守在我们上方36000公里的天疆，数36000用科学记数法表示为（）

A、 360×10² B、36×10³ C、3.6×10⁴ D、0.36×10⁵

查看试题解析
6. 下列各式符合代数式书写规范的是（）

A、 $a^{2} \times 2$ B、 $5 \frac{1}{3} m$ C、 $\frac{s}{t}$ D、2a个＋3个

查看试题解析
7. 多项式 $x^{2} - 3 k x y - 3 y^{2} + \frac{1}{3} x y - 8$ 合并同类项后不含xy项，则k的值是（）

A、 $\frac{1}{3}$ B、 $\frac{1}{6}$ C、 $\frac{1}{9}$ D、0

查看试题解析
8. 如图所示，图①中的多边形(边数为12)是由等边三角形“扩展”而来的，图②中的多边形是由正方形“扩展”而来的，…，依此类推，则由正n边形“扩展”而来的多边形的边数为（）．

A、n(n－1) B、n(n＋1) C、(n＋1)(n－1) D、n²＋2

查看试题解析

二、填空题

9. 把 $(- 3) \times (- 3) \times (- 3)$ 写成幂的形式是，底数是，指数是．

查看试题解析
10. 单项式 $\frac{5 a b^{2}}{2}$ 系数是，次数是．

查看试题解析
11. 计算 $(- 1) - (- 9) + (- 9) - (- 6)$ 的结果是．

查看试题解析
12. 数轴上到数1点的距离等于6的点所表示的数是（）．

查看试题解析
13. 若代数式 $3 x^{m} y^{3}$ 与 $- 5 x^{2} y^{n}$ 是同类项，则 $m + n$ 的值是．

查看试题解析
14. 一个单项式加上 $- 2 y^{2} + x^{2}$ 后等于 $x^{2} + y^{2}$ ，则这个单项式为．

查看试题解析
15. 若 $x = 3$ 时，代数式 $a x^{3} + b x$ 的值为12，则当 $x = - 3$ 时，代数式 $a x^{3} + b x + 100$ 的值为．

查看试题解析
16. 如图为某正方体的展开图，已知该正方体上x与y的值分别和它对面上的数字互为相反数，则2x﹣y的值为．

查看试题解析

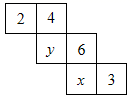
三、解答题

17. 计算：

(1)、 $26 - 7 + (- 6) + 17$

(2)、 $12 \div (- 2)^{2} + \frac{1}{4} \times (- 8)$

(3)、 $(\frac{2}{3} - \frac{3}{4} + \frac{1}{6}) \times (- 36)$

(4)、 $- 1^{4} - \frac{1}{6} \times | 2 - (- 3)^{2} |$

查看试题解析
18. 先化简，再求值： $2 (4 a^{2} - 3 a) - 3 (1 - 2 a + 4 a^{2})$ ，其中 $a = - 2$ ．

查看试题解析
19. 为鼓励市民节约用水，某地推行阶梯式水价计费制，标准如下：每户居民每月用水不超过17立方米的按每立方米a元计费；超过17立方米而未超过30立方米的部分按每立方米b元计费；超过30立方米的部分按每立方米c元计费．

(1)、若某户居民在一个月内用水15立方米，则该用户这个月应交水费多少元？

(2)、若某户居民在一个月内用水28立方米，则该用户这个月应交水费多少元？

(3)、若某户居民在一个月内用水35立方米，则该用户这个月应交水费多少元？

查看试题解析
20. 已知由几个大小相同的小立方块搭成的几何体，从上面观察，看到的形状如图所示，其中小正方形中的数字表示在该位置的小立方块的个数，请分别画出从正面、左面看到的这个几何体的形状图（几何体中每个小立方块的棱长都是1cm）画图时要用刻度尺．

查看试题解析
21. 某粮库3天内粮食进、出库的吨数如下（“+“表示进库﹣”表示出库）+25，﹣22，﹣14，+35，﹣38，﹣20

(1)、经过这3天，仓库里的粮食是增加了还是减少了？）

(2)、经过这3天，仓库管理员结算时发现库里还存280吨粮，那么3天前仓库里存粮多少吨？

(3)、如果进出的装卸费都是每吨5元，那么这3天要付多少装卸费？

查看试题解析
22. 操作探究：小明在一张长条形的纸面上画了一条数轴（如图所示），

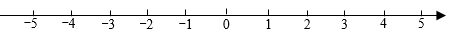(1)、操作一：折叠纸面，使1表示的点与－1表示的点重合，则－3表示的点与表示的点重合；

(2)、操作二：重新折叠纸面，使－1表示的点与5表示的点重合，请你回答以下问题：
①－3表示的点与数表示的点重合；
②若数轴上A、B两点之间距离为14，其中A在B的左侧，且A、B两点经折叠后重合，则A表示的数是， B表示的数是．

查看试题解析
23. 已知下图为一几何体从三个方向看到的形状图；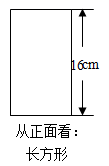

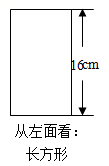
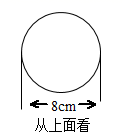(1)、写出这个几何体的名称；

(2)、画出它的表面展开图；

(3)、根据图中所给的数据，求这个几何体的表面积．（结果保留 $π$ ）

查看试题解析
24. 为丰富校园体育生活，某校增设网球兴趣小组，需要采购某品牌网球训练拍30支，网球x筒（x＞30）．经市场调查了解到该品牌网球拍定价100元/支，网球20元/筒．现有甲、乙两家体育用品商店有如下优惠方案：
甲商店：买一支网球拍送一筒网球；

乙商店：网球拍与网球均按则90%付款，

(1)、方案一：到甲商店购买，需要支付元；方案二：到乙商店购买，需要支付元（用含x的代数式表示）

(2)、若x＝100，请通过计算说明学校采用以上哪个方案较为优惠．

(3)、若x＝100，如果到甲店购买30支球拍（送30筒球），剩余的网球到乙店购买，能更省钱吗？如果可以省钱，请直接写出比方案一省多少钱？

查看试题解析